Исследование процессов дискретизации и восстановления сигналов (теорема Котельникова)

ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра «Электрической связи»

  Отчет по лабораторной работе №3

«Исследование процессов дискретизации и восстановления сигналов (т. Котельникова)»

Выполнил:

ст. гр. АТ-303

Муксимов Р. В.

Санкт – Петербург

2005г.

Задание к работе

Вариант №50

Исследуемый сигнал задан следующей функцией:

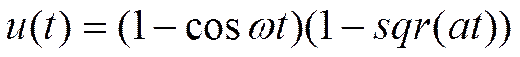, где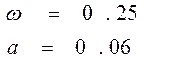

Спектр сигнала ограничен частотой W=p(рад/с), длительность сигнала Тс=16(с).

Период дискретизации вычисляется по формуле:

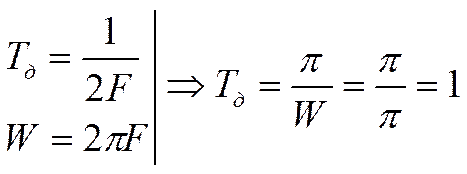
Количество участков разбиения:

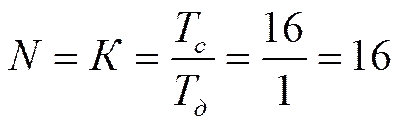
Программа работы:

1.  Исследование дискретного сигнала

1.1  Получение графика идеального сигнала

1.2  Получение графика дискретного сигнала

1.3  Получение графика восстановленного сигнала

1.4  Получение графика погрешности восстановления дискретного сигнала

2.  Исследование квантованного сигнала

2.1  Получение графиков квантованного сигнала полученных для следующих уровней квантования: n₁=16, n₂=128, n₃=512

2.2  Получение графиков восстановленного сигнала при тех же n

2.3  Получение графиков погрешности восстановления квантованных сигналов при тех же n

Все полученные графики представлены в приложении.

ПРИЛОЖЕНИЕ

1.  График идеального сигнала

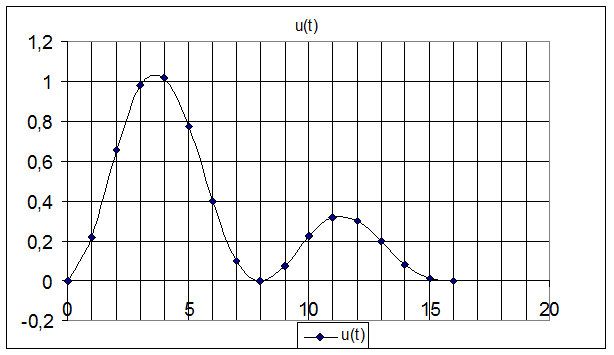
2.  График дискретного сигнала

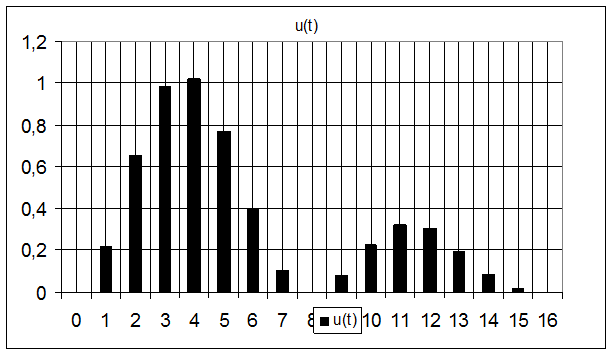
3.  График восстановленного сигнала

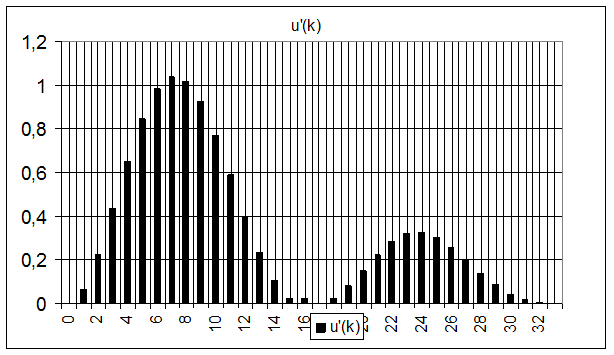
4.  График погрешности восстановления дискретного сигнала

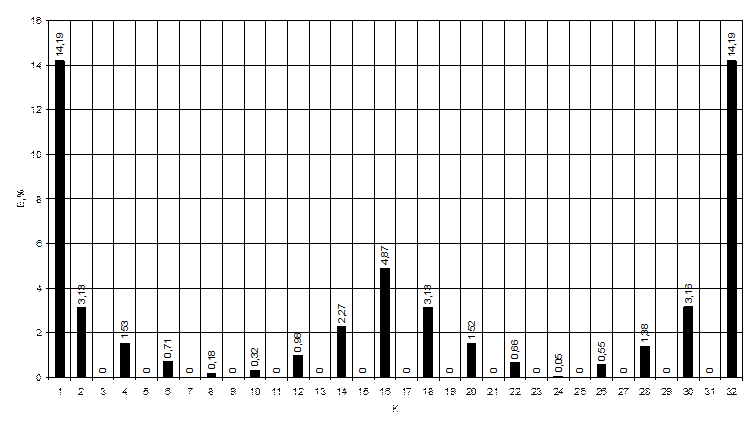
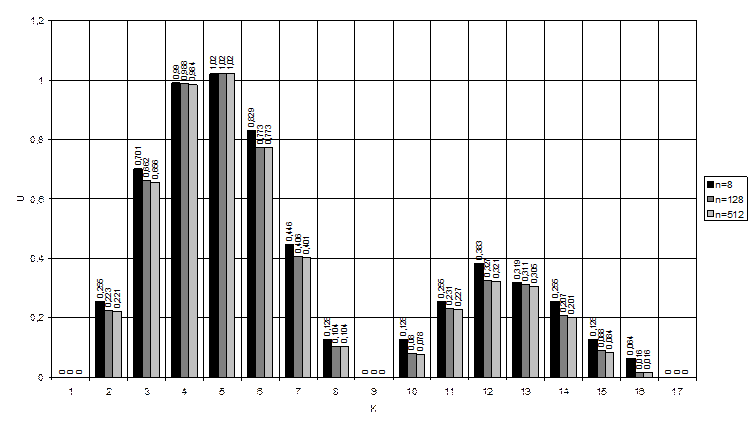
Графики квантованного сигнала полученные при: n₁=32, n₂=128, n₃=512

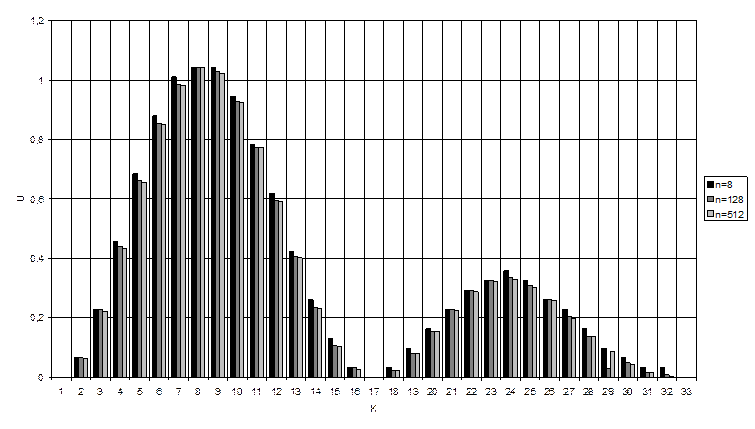
5.  Графики восстановленного сигнала полученные при: n₁=32, n₂=128, n₃=512

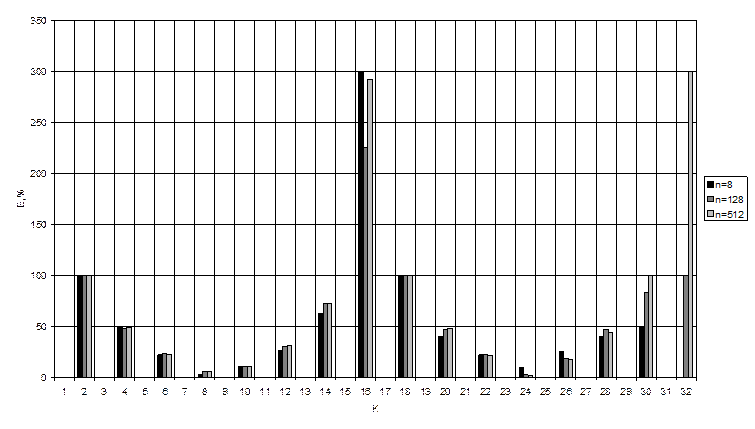
6.  Графики погрешности восстановления квантованного сигнала  при: n₁=32, n₂=128, n₃=512

Выводы

Положение максимумов погрешности в середине графика объясняется тем, что ряд Котельникова ограничен. Теорема Котельникова дает лишь предельные (потенциальные) соотношения для определенных идеализированных условий, основными из которых являются ограниченность спектра и бесконечное время наблюдения. Достичь данных предельных отношений невозможно, к ним можно только стремиться. Высокие погрешности по краям объясняются ограниченностью ряда. В середине ряд   менее ограничен, чем по краям, но т.к. амплитуда сигнала мала, то погрешности также высоки.

При увеличении числа уровней квантования точность восстановления сигнала возрастает. Наибольшее соответствие с идеальным сигналом, в данной работе, имеет восстановленный с числом уровней квантования Р=512.