Определение параметров сигналов и устройств системы передачи информации (количество информации, передаваемой за сеанс связи - 4800 бит, количество информационных элементов в комбинации - 9)

сумматоров по модулю 2, число которых равно числу знаков сложения в производящем многочлене g(x).

g(x) = x⁵+x⁴+x³+1.            

Схема кодера будет иметь следующий вид :

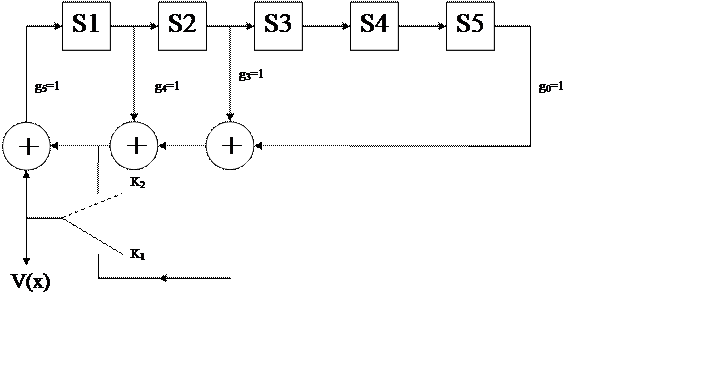
Рис. 2.

Таблица состояний элементов регистра сдвига кодера систематического (n,k)-кода.

Для описания работы схемы кодера составляются уравнения функционирования элементов регистра сдвига. При этом вводится понятие задержки на один такт. Запаздывание на один такт обозначим символом D. Тогда функционирование схемы будут определять следующие уравнения.

Работа кодирующей схемы, представленной на рис.2, при подаче на ее вход комбинации l=101000101 поясняется табл. 1. В этой таблице:

K₁ :  S1=D( L(x)+ S1+S2+S5 );

        S2=D(S1);

        S3=D(S2);

        S4=D(S3);

        S5=D(S4);

        V(x)=L(x);

 K_2: S1=0;

                 S2=D (S1);

                 S3=D (S2);

                S4=D (S3);

                S5=D (S4);

               V(x) = S1+S2+S5

                                                                                                        Таблица 1

№ такта	положение ключа	L(x)	Состояние ячеек регистра					Состояние ячеек регистра	Состояние ячеек регистра
			S1	S2	S3	S4	S5
1	K1	1	0	0	0	0	0	1	l(x) идет в   канал
2		0	1	0	0	0	0	0
3		1	1	1	0	0	0	1
4		0	1	1	1	0	0	0
5		0	0	1	1	1	0	0
6		0	1	0	1	1	1	0
7		1	0	1	0	1	1	1
8		0	1	0	1	0	1	0
9		1	0	1	0	1	0	1
10	K2	0	0	0	1	0	1	1	R(x) идет в канал
11		0	0	0	0	1	0	0
12		0	0	0	0	0	1	1
13		0	0	0	0	0	0	0
14		0	0	0	0	0	0	0

            Полученная кодовая комбинация целиком совпадает с теоретически полученной комбинацией.

Теоретические синдромы одиночной и  двойной смежной ошибки.

Общий принцип обнаружения и исправления ошибок при использовании циклического кода заключается в том, что при ошибках деление на приёмной станции идёт с остатком, и если разным ошибкам соответствуют разные остатки, последние используются как синдромы. Синдром ошибки может быть теоретическим, а может быть аппаратным. Обычно они не совпадают. 

Одиночные ошибки.

e(x) = x^n-1                                e(x) разделим на g(x)

           

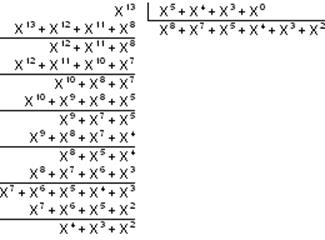
                                    R (x) = 00111

Проведем модификацию синдрома по формуле :

(x^n-1 * x^n-k  ) ÷ g(x)

     

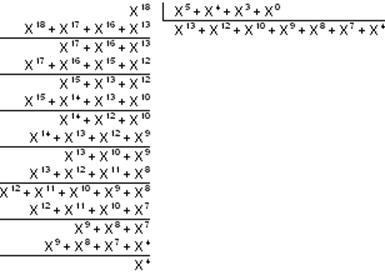
                                          R (x) = 00001                 

Двойные ошибки.

(x^n-1+ x^n-2 )  ÷ g(x)

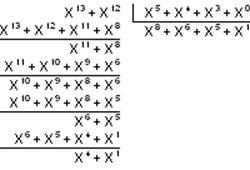
                       R (x) = 01001

Проведем модификацию синдрома по формуле :

(x^n-1 * x^n-k+ x^n-2 * x^n-k  )  ÷   g(x)

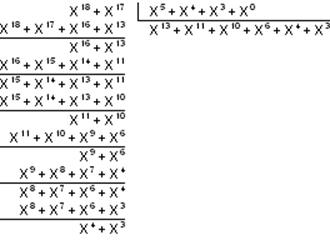
                                  R (x) = 00011 

Структурная схема генератора синдрома систематического (n,k)-кода.

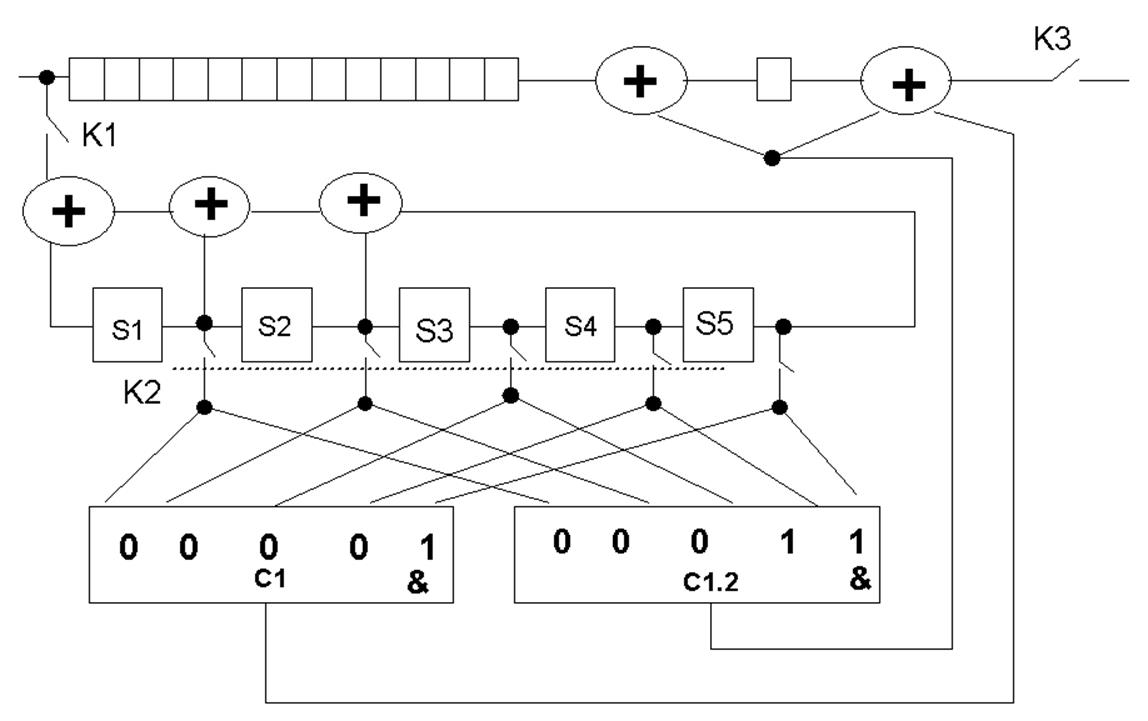
            Схема генератора синдромов представляет собой схему деления. Она состоит из тех же элементов, что и кодер. Построим схему генератора синдромов; она изображена на рисунке 3:

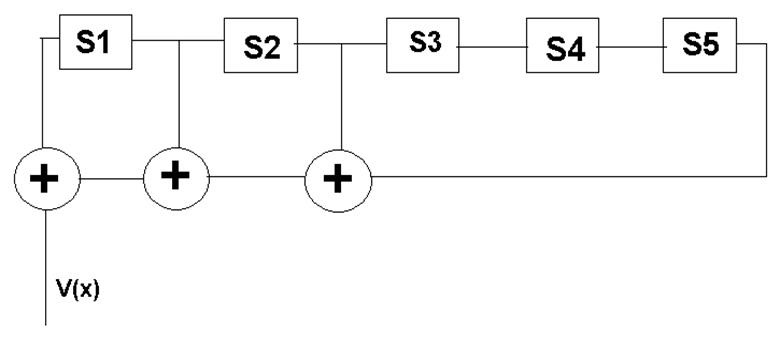
Рис. 3.

Таблица состояний для получения аппаратного синдрома построенного генератора .

Работа данной схемы описывается уравнениями:

S1=D(e(x)+ S1+ S2+ S5); S2=D(S1); S3=D(S2); S4=D(S3); S5=D(S4)

Чтобы показать, как работает схема генератора синдромов при поступлении на ее вход одиночной, двойной смежной ошибки в старшем разряде, составим по этим у

равнениям таблицы состояний регистров.

№ такта	е(x)	S1	S2	S3	S4	S5	е(x)	S1	S2	S3	S4	S5
1	1	0	0	0	0	0	1	0	0	0	0	0
2	0	1	0	0	0	0	1	1	0	0	0	0
3	0	1	1	0	0	0	0	0	1	0	0	0
4	0	0	1	1	0	0	0	1	0	1	0	0
5	0	1	0	1	1	0	0	1	1	0	1	0
6	0	1	1	0	1	1	0	0	1	1	0	1
7	0	1	1	1	0	1	0	0	0	1	1	0
8	0	1	1	1	1	0	0	0	0	0	1	1
9	0	0	1	1	1	1	0	1	0	0	0	1
10	0	0	0	1	1	1	0	0	1	0	0	0
11	0	1	0	0	1	1	0	1	0	1	0	0
12	0	0	1	0	0	1	0	1	1	0	1	0
13	0	0	0	1	0	0	0	0	1	1	0	1
14	0	0	0	0	1	0	0	0	0	1	1	0
15	0	0	0	0	0	1	0	0	0	0	1	1

                                                                                               Таблица 2.

Таблица состояний элементов регистров сдвига генератора синдрома декодера на примере ошибочно принятой кодовой комбинации.

Проверим работу генератора на примере ошибочной комбинации. Теперь подадим на вход генератора синдромов комбинацию V(x) допустив сначала ошибку во втором такте   (ля одиночных ошибок), а потом во втором и третьем такте ( для двойных смежных ошибок).

S1=D(V(x)+ S1+S2+S5); S2=D(S1); S3=D(S2); S4=D(S3); S5=D(S4)

Функционирование схемы в этом случаи представлено в таблице 3:

                                                                                                                      Таблица 3.

№ такта	V(x)	S1	S2	S3	S4	S5	V(x)	S1	S2	S3	S4	S5
1	1	0	0	0	0	0	1	0	0	0	0	0
2	0	1	0	0	0	0	0	1	0	0	0	0
3	1(0)	1	1	0	0	0	1(0)	1	1	0	0	0
4	0	0	1	1	0	0	0(1)	0	1	1	0	0
5	0	1	0	1	1	0	0	0	0	1	1	0
6	0	1	1	0	1	1	0	0	0	0	1	1
7	1	1	1	1	0	1	1	1	0	0	0	1
8	0	0	1	1	1	0	0	1	1	0	0	0
9	1	1	0	1	1	1	1	0	1	1	0	0
10	1	1	1	0	1	1	1	0	0	1	1	0
11	0	0	1	1	0	1	0	1	0	0	1	1
12	1	0	0	1	1	0	1	0	1	0	0	1
13	0	1	0	0	1	1	0	1	0	1	0	0
14	0	0	1	0	0	1	0	1	1	0	1	0
15	0	0	0	1	0	0	0	0	1	1	0	1
16	0	0	0	0	1	0	0	0	0	1	1	0
17	0	0	0	0	0	1	0	0	0	0	1	1

Из таблицы видно, что обнаружение ошибки происходит на такте n+y,

где y – номер такта, с которого начинается ошибка, будь то одиночная или двойная смежная ошибка.

Расчет амплитуды импульсов на входе канала ТУ. Расчет длительности импульсов.

Данные для расчета амплитуды и длительности импульса (из задания):

·  Действующее напряжение помехи на выходе канала ТУ D =15(мВ)

·  Вероятность ошибки на выходе канала ТУ

·  Затухание канала ТУ  а =19(дБ)

·  Время опроса Топр =6.3 мин

·  Количество информации передаваемой за один сеанс связи I =4800(бит)

Uвх = А – амплитуда импульсов на входе

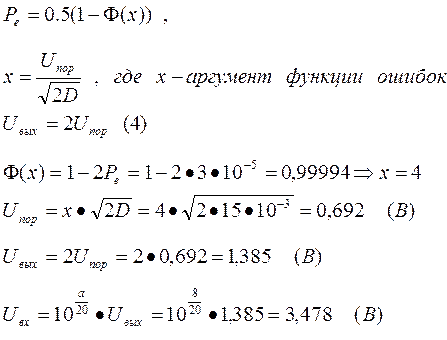
Длительность импульса определяется из выражения:

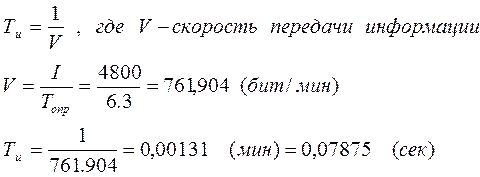
Передаточная функция фильтра, согласованного с одиночными импульсами.

Согласно исходным данным, информация по каналу ТУ передаётся импульсами 1+.

Передаточная функция фильтра находится по следующему алгоритму:

1.  Найти спектр сигнала, с которым фильтр согласован:

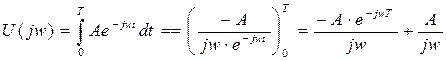
2.  Записать передаточную функцию:

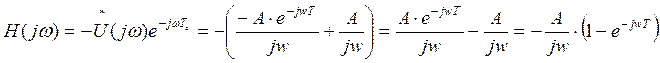
Подставив Т =  0,0078 мин и А = 3,478 В получим:

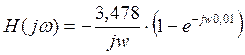
Структурная схема согласованного фильтра.

Схему согласованного фильтра строят по передаточной функции H(jw). Умножение на 1/jw соответствует интегрированию; умножение на e^-jwT соответствует задержке сигнала на Т.

- интегратора с коэффициентом передачи 1/jw

- линии задержки на время Т с коэффициентом передачи е^-jwT;

- вычитающего устройство.

Схема согласованного фильтра для импульса 1 +  представлена на рисунке 5:

 

∫dt

U(t)

 

	Рис. 5

 

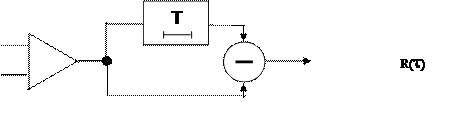Заметим, что на выходе  согласованного фильтра получаем сигнал, являющейся автокорреляционной функцией входного сигнала.

Структурная схема фильтра, согласованного с комбинацией синхросигнала (функция автокорреляции).

Чтобы построить схему согласованного фильтра, необходимо знать