Вариант №3.
А А А В А А А Б Б В А А А Б В В А А А Б
А В В А А А Б В В А Б А А А Б В А А А Б
Б В А А А Б В В В В А А А В В В В А А А
Б А Б А В В А А А Б А А А Б Б А В Б Б Б
А А А В А А А А В Б В А А В А А Б Б В В
1. Определение статистических характеристик источника информации по заданному его сообщению.
Длина сообщения n=100, число букв в алфавите N=3, их перечень А=(А,Б, В)
Вероятность появления букв в сообщении.
|
Ai |
Ni |
Pi |
|
А |
52 |
0,52 |
|
Б |
21 |
0,21 |
|
В |
27 |
0,27 |
Вероятность двубуквенных сочетаний.
|
AiAj |
Nij |
Pij |
PiPj |
|
АА |
31 |
0,31 |
0,27 |
|
АБ |
13 |
0,13 |
0,11 |
|
АВ |
8 |
0,08 |
0,14 |
|
ББ |
6 |
0,06 |
0,05 |
|
БВ |
8 |
0,08 |
0,06 |
|
БА |
7 |
0,07 |
0,11 |
|
ВВ |
11 |
0,11 |
0,07 |
|
ВБ |
2 |
0,02 |
0,06 |
|
ВА |
14 |
0,14 |
0,14 |
Марковский источник, т. к. Pij не равно PiPj.
Переходные (условные) вероятности P(Ai/Aj).
|
Последующие буквы Aj |
||||
|
А |
Б |
В |
||
|
Предыдущие буквы Ai |
А |
0,596 |
0,25 |
0,154 |
|
Б |
0,333 |
0,286 |
0,381 |
|
|
В |
0,519 |
0,074 |
0,407 |
|
Сумма этих вероятностей в каждой строке таблицы должна равняться единице.
Граф функционирования Марковского источника.
2.Определение информационных характеристик источника и оценка влияния на них неравновероятности и взаимозависимости букв.
Значения энтропии источника:
- В предположении равновероятности и взаимонезависимости букв
log2N=log23=1.585
- Без учета взаимозависимости букв
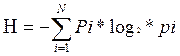
- С учетом взаимозависимости букв
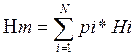, где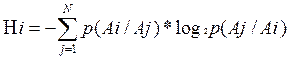 
Характеристика источника.
|
Использованная модель источника |
|||
|
Марковская |
С независимыми буквами |
С равновероятными и независимыми буквами |
|
|
Энтропия Н, бит/букву |
1,388 |
1,437 |
1,585 |
|
Относительная избыточность Е, % |
0,124 |
0,071 |
0 |
|
Информативность Д |
0,876 |
0,929 |
1 |
Степень уменьшения энтропии показывает число букв переносимых источником. Наличие наибольшего числа букв в сообщении, чем это минимально необходимо вызвано наличием неравновероятного и взаимозависимого появления букв.
Количество информации в сообщении J=n*H=100*1.58=158,5 минимальное количество двоичных символов nmin=n*H=100*1.585=158
Число двоичных букв 2Кравн≥N, N=3, Кравн=2
3. Статистическое кодирование сообщений источника.
Необходимо для исключения избыточности.
Построение статистического кода по алгоритму Фэно.
|
Ai |
Pi |
1 |
2 |
Кодовая комбинация |
Число символов |
|
А |
0,52 |
1 |
1 |
1 |
|
|
В |
0,27 |
0 |
1 |
01 |
2 |
|
Б |
0,21 |
0 |
0 |
00 |
2 |
|
AiAj |
PiPj |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
Кодовая комбинация |
Число символов |
|
АА |
0,31 |
1 |
1 |
2 |
||||||
|
ВА |
0,14 |
1 |
0 |
2 |
||||||
|
АБ |
0,13 |
0 |
1 |
1 |
3 |
|||||
|
ВВ |
0,11 |
0 |
1 |
0 |
1 |
4 |
||||
|
АВ |
0,08 |
0 |
1 |
0 |
0 |
4 |
||||
|
БВ |
0,08 |
0 |
0 |
1 |
1 |
4 |
||||
|
БА |
0,07 |
0 |
0 |
1 |
0 |
4 |
||||
|
ББ |
0,06 |
0 |
0 |
0 |
1 |
4 |
||||
|
ВБ |
0,02 |
0 |
0 |
0 |
0 |
4 |
Вычислить количество букв статистического кода, необходимое для кодирования стобуквенного сообщения источника.
nст1=52*1+27*2+21*2=148
nст2 = (31*2+14*2+13*3+11*4+8*4+8*4+7*4+6*4+2*5)/2 = 144,5
Остаточная избыточность и информативность сообщения после статистического кодирования его.
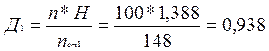Е=0,062
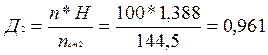Е=0,039
Побуквенное статистическое кодирование существенно уменьшает только избыточность, возникающую за счет неравновероятности букв, не влияет на избыточность, определяемую взаимозависимостью букв.
Эффективность статистического кодирования.
|
Модель источника |
||
|
Марковская |
||
|
nмин |
||
|
E |
0,124 |
|
|
Еост |
При стат. кодировании по буквам |
0,062 |
|
То же, по двубуквенным сочетаниям |
0,039 |
|
Вывод: при кодировании источника по двубуквенным сочетаниям
снижается избыточность, по сравнению с отдельными буквами.
МПС
ПГУПС
Кафедра «Электрическая связь»
Лабораторная работа №5
Тема: «Исследование дискретного источника информации»
|
Выполнил: Елгашин А. В. АТТ-104 Проверил: |
Вариант №3
Санкт-Петербург
2003г.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.