Анализ работы механической системы, страница 3

Кинематическая пара (нематериальное понятие) – подвижное соединение двух звеньев.

Кривошип – звено поворачивающееся на 360⁰.

Для анализа работы механической системы была выбрана схема, изображенная на рис. 1.

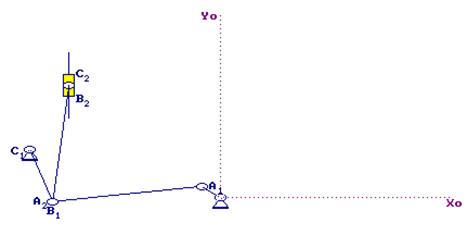
Рис. 1

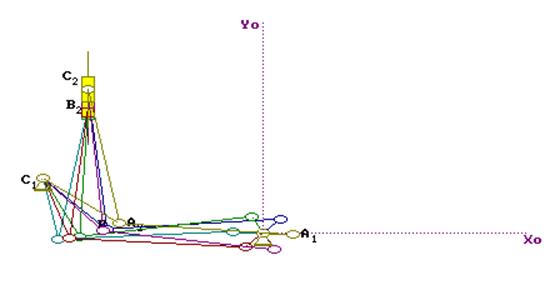
Рис. 2

2.2 Проверка работоспособности механизма.

Можно проверить двумя способами: аналитически и по формуле Чебышева.

Рассчитаем работоспособность механизма формульным методом:

W = 3·(n - 1) - 2p₁ , где W – степень подвижности, р₁ – число одноподвижных кинематических пар

n – 1 – число подвижных звеньев

W = 3·(6 - 1) - 2·7 = 15 – 14 = 1

Вывод:  Согласно полученному результату механизм работоспособен и для его работы необходим один двигатель.

Проверка работоспособности графическим методом сделана в приложении 1 (лист формата А3). Выполнено построение 6 положений механизма, начальный угол равен 0⁰.

3. Кинематика преобразовательного механизма.

3.1 Закон движения кривошипа.

Угловая скорость движения кривошипа вычисляется по формуле:

ω_кр=n/9.55 , где n – число об/мин.

По заданию:

ω_кр=142/9.55=14,869 1/с.

В разделе «Кинематический анализ» определить скорость и ускорение исполнительного органа.   Выписать скорость и ускорение исполнительного органа для 240⁰ или 300⁰.  Для данного механизма было взято 240⁰.

Были получены результаты:

V_d = 0.19912 м/с

a_d  = 3.2585 м/с².

   Таблица 1

Перемещения			Скорость			Ускорения
№	Fi, град.	X, м	№	Fi, град.	V, м/с	№	Fi, град.	a, м/с2
0	0	0	0	0	0	0	0	-7.4078
1	60	-0,012304	1	60	-0,26912	1	60	-0,88466
2	120	-0,030696	2	120	-0,21896	2	120	2.0530
3	180	-0,039891	3	180	-0,034754	3	180	2.7491
4	240	-0,035330	4	240	0,17075	4	240	3.2293
5	300	-0,015967	5	300	0,34715	5	300	0,24002
6	360	-1.0345e-012	6	360	0	6	360	-7.4078

Графики перемещения, скорости и ускорения исполнительного органа (ползуна)

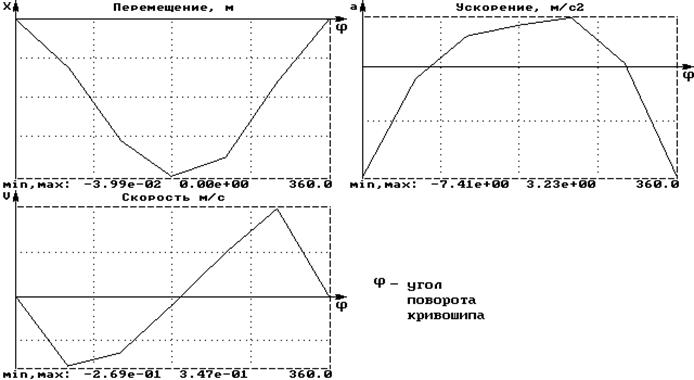
Рис. 3

3.2  Расчет скорости и ускорения графическим методом.

Был построен и выполнен расчет (см. лист формата А3)  

Получены результаты:

V_d = 0.20073 м/с

a_d  = 3.3484 м/с².

В результате расчета погрешности составили:

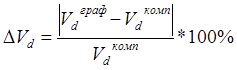   = 1%

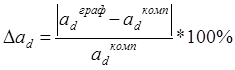 =  2.8%

4. Внешняя нагрузка.

Динамика решает задачи движения рабочей точки с учётом нагрузок действующих на механизм.

Нагрузки бывают:

1.  Движущая (T_дв)

2.  Сопротивления.

В свою очередь сопротивление делится на:

а) полезное б) вредное (обусловлено трением)

4.  Инерционные (неравномерности движения)

Полезное сопротивление в нашем задании равно F = 200 Н.   Но было введено другое сопротивление 5500 Н или 5,5 кН.  Это можно объяснить тем, что двигателя с требуемой мощностью нет в катологе (по каталогу ЭД  - двигатели от 0,5 кВт). Вследствие чего была увеличили нагрузка на рабочий орган, после чего получили мощность Р = 0,709 кВт, что удовлетворяет условию.

Выбираем построение из 36 строк, т.е через каждые 10⁰.

График задания внешней нагрузки

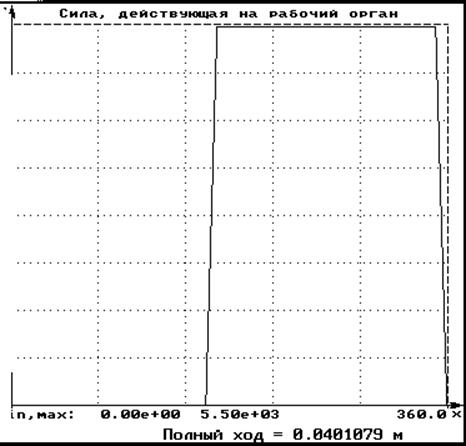
Рис. 4

Максимальный момент:   М_max = 128, 477 [Н*м]

Раннее говорилось, что существует момент вредного сопротивления, который равен 10% от максимального момента. M_BC = 12,477 [Н*м]. Учтем его при построении графика.

В результате чего, получаем графики приведенного момента нагрузки без учета вредного сопротивления и с учетом вредного сопротивления.

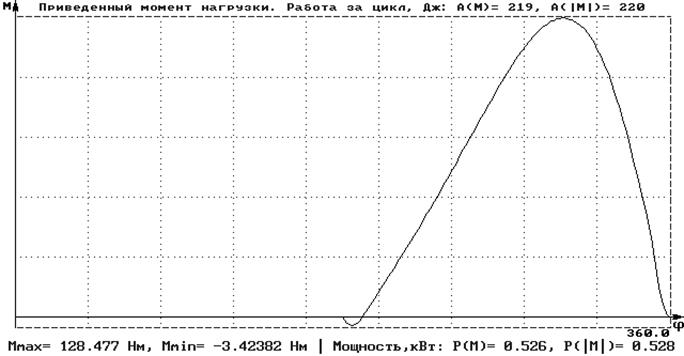
Рис. 5

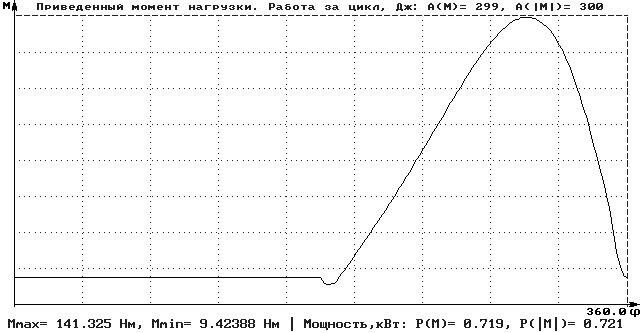
Рис. 6

                                                         Таблица 2

Выборка из таблицы нагрузки
Fi, град.	Мпр, Н*м
240	76,001

Максимальный момент:   М_max = 141,325 Н*м.

Мощность: Р = 0,709 кВт.

Далее было выписан момент при 240⁰ для сравнения с расчётным.