Расчет переходных процессов в линейной электрической цепи, страница 2

Преобразуем схему изображенную на рисунке 2.1 в схему изображенную на рисунке 2.2 для режима до коммутации:

 

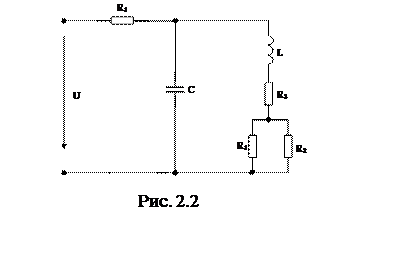Процесс до начала коммутации, рассчитаем сопротивления:

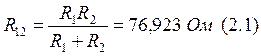
Перерисуем схему рассчитываемой цепи до коммутации, при условии, что эквивалентное сопротивление подсчитано. На постоянном токе сопротивление катушки равно 0, это соответствует короткозамкнутым зажимам катушки. Постоянный ток не проходит через емкость, это соответствует разомкнутым зажимам конденсатора. Представим это на рисунке 2.3.

 

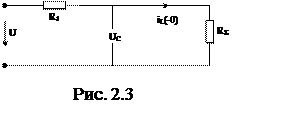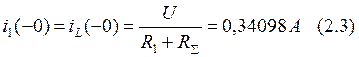
По законам коммутации:

Запишем систему уравнений, составленную законам Кирхгофа для режима после коммутации:

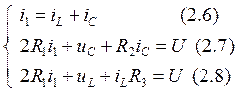
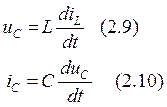
Начальные условия:

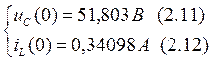
Подставим (2.6) в (2.7), тогда:

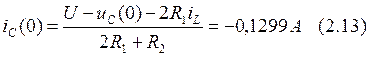
Из формулы (2.6) выразим:

Из формулы (2.7) выразим:

В установившемся режиме (t®¥):

; 

Изобразим операторную схему замещения на рисунке 2.4.

 

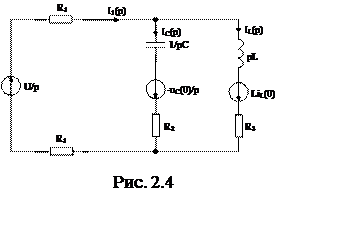Система уравнений в операторной форме записи:

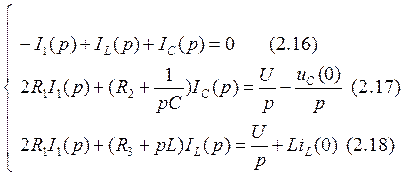
Рассчитаем главный определитель этой системы. Он будет равен:

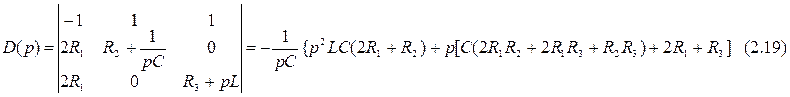
Теперь рассчитаем первый, второй и третий определители системы.

 

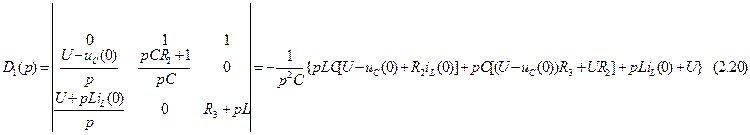
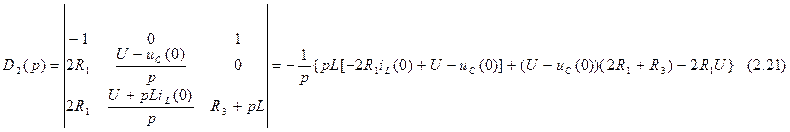
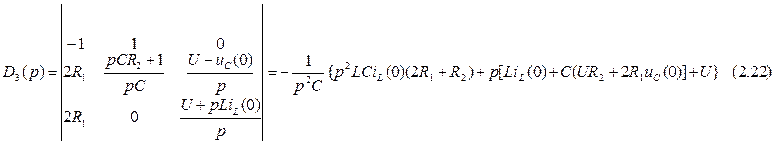
Значения токов в операторной форме можно найти по следующим формулам:

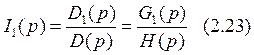
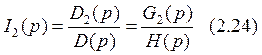
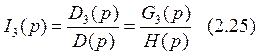
Знаменатель:

Получаем из 2.26 корни знаменателя:

p₁=-772,104; p₂=-117,181; p₃=0

Рассчитаем постоянные времени:

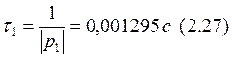
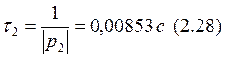
Производная знаменателя:

Отсюда получаем H’(p₁)=2654,83; H’(p₂)=-402,896; H’(p₃)=475.

Найдем числитель в операторном изображении тока I₁(p):

Отсюда получаем G₁(p₁)=-48,5457; G₁(p₂)=9,3724; G₁ (p₃)=120.

Определяем значение тока i₁ во временной области:

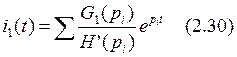
Подставим численные значения в формулу (2.30):

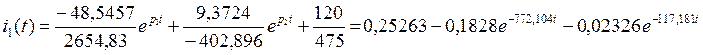
Найдем числитель в операторном изображении тока I_C(p):

Отсюда получаем G₂(p₁)=-195,952; G₂(p₂)=82,075; G₂ (p₃)=0.

Определяем значение тока i_C во временной области:

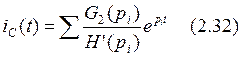
Подставим численные значения в формулу (2.32):

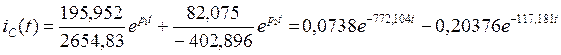
Найдем числитель в операторном изображении тока I_L(p):

Отсюда получаем G₃(p₁)=-244,5; G₃(p₂)=-72,703; G₃ (p₃)=120.

Определяем значение тока i_L во временной области:

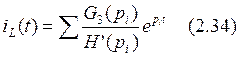
Подставим численные значения в формулу (2.34):

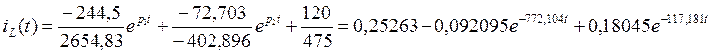
Операторные изображения напряжений на реактивных элементах получаем по следующим формулам:

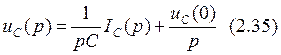
Найдем напряжения на реактивных элементах во временной области по формулам:

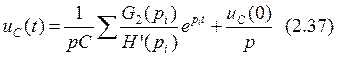
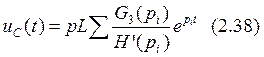
Подставляя численные значения в формулы (2.37) и (2.38) получаем напряжения на реактивных элементах:

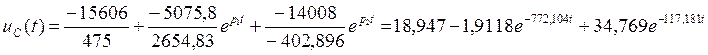
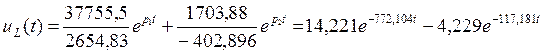
Заключение

В работе, состоящей из двух частей, был проделан расчет разветвленной цепи, содержащей  реактивные элементы, классическим методом и расчет разветвленной цепи, содержащей реактивные элементы, операторным методом.

В первой части работы был произведен расчет разветвленной цепи классическим методом. Была составлена система уравнений по законам Кирхгофа для режима после коммутации. Корни характеристического уравнения определены при помощи нахождения входного сопротивления Z(p). Далее были определены постоянные интегрирования. Для этого была составлена система из двух уравнений. Для составления системы использовались законы коммутации для тока в катушке и напряжения на конденсаторе, а также рассматривалась схема в режиме до коммутации. Напряжение на катушке, а также ряд других величин, не подчиняющихся законам коммутации, были найдены с использованием уравнений, составленных по  законам Ома и Кирхгофа. Итак, найденные величины равны:

1.  p₁ = -696,1308

2.  p₂ = -53,8692

3. 

4. 

5. 

6. 

7.       

Во второй части работы был произведен расчет разветвленной цепи операторным методом. Необходимые для расчета величины напряжения на конденсаторе в момент коммутации и тока в индуктивности в момент коммутации найдены с использованием законов коммутации. Затем найденные значения величин, а также необходимые исходные данные были подставлены в начальную систему уравнений. Для нахождения токов, протекающих в ветвях схемы, были составлены и вычислены главный, первый, второй и третий определители системы. Затем были найдены выражения токов  в операторной форме. С применением теоремы разложения были найдены значения токов во временной области. Итак, найденные величины равны:          

1.  p₁ = -772,104

2.  p₂ = -117,181

3.  p₃ =0

4. 

5. 

6. 

7. 

8. 

Список используемых источников

1.  Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники, т.1.      – Л.: Энергоиздат, 1981. –536 с.