Расчет переходных процессов в линейной электрической цепи

Министерство Путей Сообщения Российской Федерации

Петербургский Государственный Университет Путей Сообщения

Кафедра «Теоретические основы электротехники»

Домашнее задание

«Расчет переходных процессов в линейной электрической цепи»

Выполнил студент группы АТК-102

Лебединский А.А.

Проверил преподаватель

Курмашев С.М.

Санкт-Петербург

2002

Содержание

Перечень условных обозначений  3

Введение  4

1.   Расчет разветвленной цепи классическим методом   5

2.   Расчет разветвленной цепи операторным методом   7

Заключение  12

Список используемых источников  13

Перечень условных обозначений

– сопротивление

– индуктивность

– емкость

– ключ

p₁, p₂, p₃ – корни характеристического уравнения

t₁, t₂ – постоянные времени

i_C, i_L, i₃ – токи, протекающие в ветвях  при расчете  классическим методом

u_C – напряжение на емкости

u_L – напряжение на индуктивности

U – входное напряжение цепи

A₁, A₂ – постоянные интегрирования

R₁, R₂, R₃ – сопротивления

L – индуктивность

С – емкость

I₁(p), I_C(p) ,I_L(p) – токи, протекающие в ветвях при расчете операторным       методом

u_C(0) – напряжение на конденсаторе в момент коммутации

u_L(0) – напряжение на индуктивности в момент коммутации

i_L(0) – ток в индуктивности в момент коммутации

Введение

Целью данной работы является расчет разветвленной цепи, содержащей реактивные элементы, классическим и операторным методами. Дана разветвленная электрическая цепь с двумя реактивными элементами, на ней указан вид коммутации, вызывающий переходный процесс.

Исходные данные, необходимые для расчета цепи классическим методом, приведены в таблице 1.

Таблица 1

Исходные данные для расчета цепи классическим методом

Схема цепи, рассчитываемая классическим методом в первой части работы, представлена на рисунке 1.

 

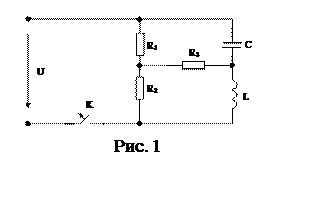Исходные данные, необходимые для расчета цепи операторным методом, приведены в таблице 2.

Таблица 2

Исходные данные для расчета цепи операторным методом

Схема цепи, рассчитываемая операторным методом во второй части работы, представлена на рисунке 2.

 

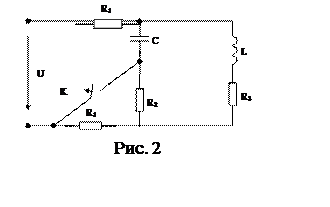1.  Расчет разветвленной цепи классическим методом

Рассчитаем значения токов, протекающих в ветвях, и  напряжений на реактивных элементах для схемы, изображенной на рисунке 1.1.

         

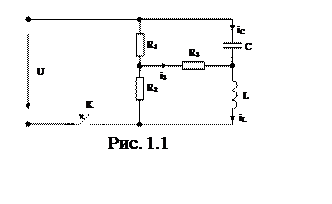
Процесс до коммутации, сосчитаем R₂₃:

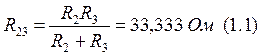
Ток цепи равен:

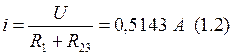
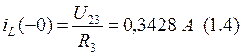
Составим для цепи исходную систему уравнений по законам Кирхгофа:

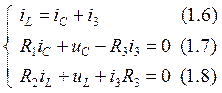
Из (1.6) выразим:

Начальные условия (t=0):

Подставим (1.6) в (1.7):

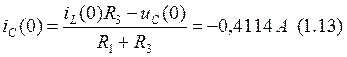
Установившиеся (принужденные) значения нулевые, т.к. цепь остается без источника питания после размыкания ключа. Для определения корней характеристического уравнения рассчитаем входное сопротивление цепи Z(p).

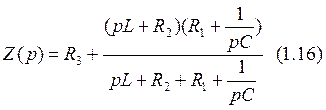
Þ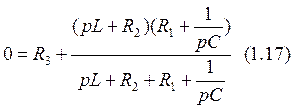

Приведем слагаемые к общему знаменателю, получим рациональную дробь, числитель которой приравняем нулю и решим квадратное уравнение относительно p:

Подставляя в формулу  (1.18)  численные значения, получаем:

Отсюда получаем, что p₁ = -696,1308; p₂ = -53,8692.

Найдем постоянные времени:

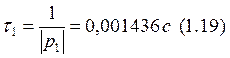
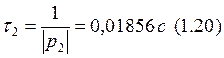
Искомая величина тока на индуктивности определяется по формулам:

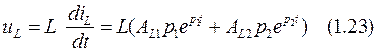
Решая (1.24) найдем постоянные интегрирования:

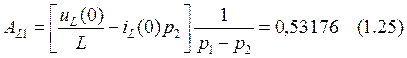
Подставляем A_L1 в формулу (1.22) и получаем:

Подставляем полученные значения в формулу (1.21) и находим ток на индуктивности:

Искомая величина напряжения на индуктивности определяется по формуле (1.23):

Искомая величина напряжения на емкости определяется по формулам:

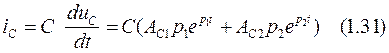
Решая (1.32) найдем постоянные интегрирования:

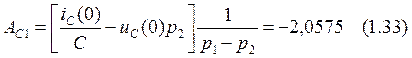
Подставляем A_С1 в формулу (1.30) и получаем:

Подставляем полученные значения в формулу (1.29) и находим напряжение на емкости:

Искомая величина тока на емкости определяется по формуле (1.31):

Теперь найдем ток i₃ из уравнения (1.9). Подставив в это уравнение значения токов i_L и i_C. Получаем следующее:

2.  Расчет разветвленной цепи операторным методом

Схема цепи, расчет которой производится операторным методом, представлена на рисунке 2.1.