Исследование дискретной системы управления, определение показателей качества

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ДОНБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

КАФЕДРА АУТП

ОТЧЕТ

по лабораторной работе 1

Исследование дискретной системы управления

По курсу «Цифровые системы управления»

Выполнила: ст.гр. АКГ-09

Суховиенко Д.С

Принял: доц. кафедры

Литвинов

Алчевск, 2011

ВВЕДЕНИЕ

Целью данной работы является знакомство с работой дискретных   систем, определение показателей качества.

1  ТЕОРЕТИЧЕСКИЕ   ИССЛЕДОВАНИЯ

1.1  Задания к лабораторной работе 

Используя пакет Simulink системы MATLAB исследовать работу импульсных элементов - экстраполятора нулевого и первого порядков. В качестве тестового входного сигнала принять синусоидальный сигнал единичной амплитуды частотой  ω₀ = 1 рад/c. Получить графики входного,  выходного сигналов и сигнала ошибки квантования при различных периодах   дискретизации.

Осуществить моделирование непрерывной системы управления и определить показатели качества переходного процесса при единичном скачкообразном задающем воздействии. Учесть, что время интегрирования должно быть больше времени достижения первого максимума после начала переходного процесса, т.е. больше 4.6Tμ  и меньше 10Tμ .Параметры объекта   управления К₀ =30, Т1=0,7 с, Т2=0,07 с.

Осуществить моделирование импульсной системы управления с экстраполятором нулевого порядка, установленным на выходе регулятора, и определить показатели качества переходного процесса при периодах квантования T_k = 0.1/ ω_с, T_k = 0.25/ω_с, T_k = 0.5/ω_с, T_k = 1/ ω_с. Параметры объекта управления такие же, как и  в предыдущем задании.

Осуществить моделирование импульсной системы управления с экстраполятором первого порядка, установленным на выходе регуляторе, определить показатели качества переходного процесса. Параметры объекта управления и периоды квантования такие же, как и в предыдущем задании.

1.2  Подготовка к выполнению лабораторной работы

1.2.1 Исследование работы импульсных элементов – экстраполятора нулевого и первого порядка

Структурные схемы для исследования работы экстраполяторов нулевого и  первого порядка с учетом ошибки квантования представлены на рисунках  1.1 и  1.2 соответственно.

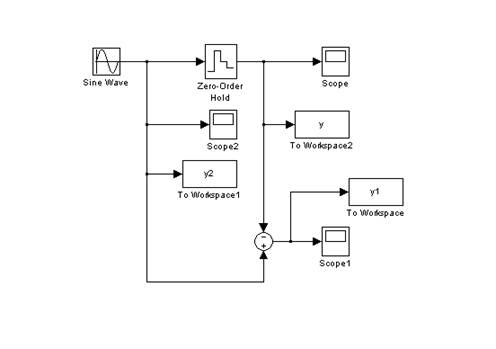
Рисунок 1.1 – Структурная схема для исследования работы экстраполятора  нулевого порядка

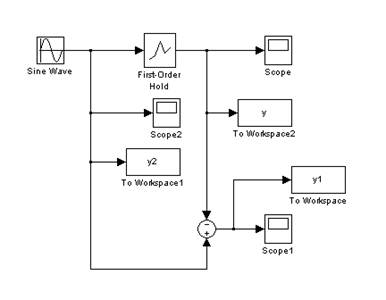
Рисунок 1.2 – Структурная схема для исследования работы экстраполятора   первого порядка с учетом ошибки квантования

Периоды квантования, при которых должна быть исследована работа  экстраполяторов, имеют следующие значения:

T_k  =1/ω₀ = 1/1=1с,

T_k =0.5/ω₀ = 0.5/1=0.5 с,

T_k =0.1/ω₀ = 0.1/1=0.1с,

T_k =0.01/ω₀ = 0.01/1=0.01с.

1.2.2 Исследование непрерывной системы управления 

Структурная схема непрерывной системы управления представлена на рисунке 1.3.

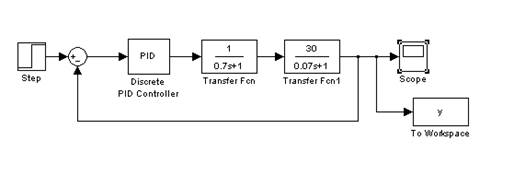
Рисунок 1.3 - Структурная схема непрерывной системы управления

Система управления состоит из объекта второго порядка и пропорционально интегрального регулятора. 

Передаточная   функция   объекта   управления

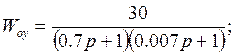
Передаточная функция пропорционально - интегрального регулятора

.

Коэффициенты пропорциональной   и интегральной  частей регулятора 

рассчитываются по формулам

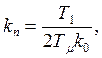
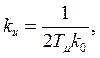
где

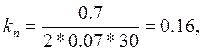
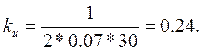
1.2.3 Исследование импульсной системы управления с экстраполятором  нулевого порядка

Структурная схема импульсной системы управления с экстраполятором  нулевого порядка представлена на рисунке  2.4.

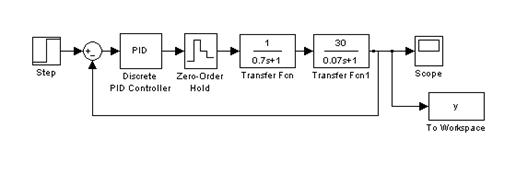
Рисунок 1.4 – Структурная схема дискретной системы управления с экстраполятором нулевого порядка

Частота среза замкнутой системы определяется выражением

.

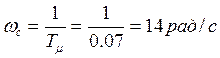Исследование системы управления производится при следующих   периодах дискретизации

T_k  =0,1/= 0,1/14=0,007с,

T_k =0.25/= 0.25/14=0.02 с,

T_k =0.5/ = 0.5/14=0.04с,

T_k =1/ = 1/14=0.07с.

1.2.4 Исследование импульсной системы управления с экстраполятором  первого порядка

Структурная схема импульсной системы управления с экстраполятором  первого порядка представлена на рисунке 1.5.

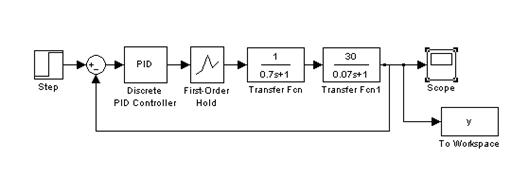
Рисунок 1.5 – Структурная схема дискретной системы управления с 

экстраполятором первого порядка

Частота среза замкнутой системы определяется выражением

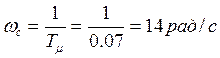
Исследование системы управления производится при следующих   периодах дискретизации

T_k  =0,1/= 0,1/14=0,007с,

T_k =0.25/= 0.25/14=0.02 с,

T_k =0.5/ = 0.5/14=0.04с,

T_k =1/ = 1/14=0.07с.