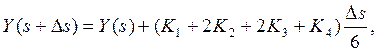Численный анализ напряженно-деформированного состояния составных оболочечных конструкций: Методические указания, страница 3

                                    (3.3)

где

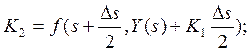
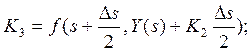
Выполнив численное интегрирование системы (3.2) по методу Рунге-Кутта (3.3) на первом участке ортогонализации  p-го оболочечного элемента, получаем решение  в узловой точке . Для обеспечения устойчивости вычислительного процесса выполняем ортонормирование матрицы решений  по формулам:

 

     

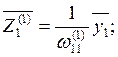
(3.4)

          

 

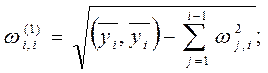
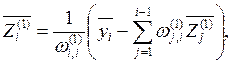
Здесь  означает скалярное произведение векторов  и ;  - первые три столбца матрицы решений .

Вектор  (четвертый столбец матрицы )  ортогонализируем  по формулам:

                  

(3,5)

     

В результате ортонормирования и ортогонализации векторов

являющихся столбцами матрицы  в точке , по формулам (3.4) и (3,5) получаем матрицы

                                           (3,6)

и

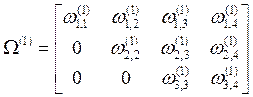                                                 (3,7)

Полученную в результате операции ортонормирования матрицу  используем в качестве начальной матрицы для численного интегрирования системы (3.2) на следующем участке ортогонализации . Выполнив интегрирование по методу Рунге-Кутта (3.3), получаем матрицу решений в точке . Эту матрицу ортонормируют по формулам (3.4), (3.5). Полученную в результате ортонормирования матрацу  используем в качестве начальной для интегрирования системы уравнений (3,2) на следующем участке ортогонализации . Выполнив последовательно интегрирование по всем участкам ортогонализации рассматриваемого р-го оболочечного элемента, получаем матрицу решений в конечной точке  элемента. Эту матрицу принимаем  в качестве начальной для следующего -го оболочечного элемента, для которого процесс прямой прогонки строим аналогично рассмотренному для -го элемента.

Учет сосредоточенных нагрузок  приложенных на границе между -м и -м оболочечными элементами в сеченая , и упругих опор, установленных в этом сечении, осуществляем в процессе прямой ортогональной прогонки с помощью следующего преобразования матрицы решений:

                                                          (3.8)

где

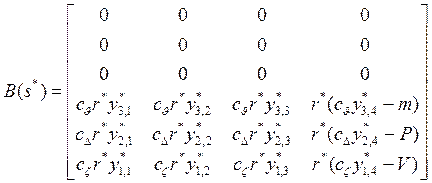                                        (3.9)

 - элементы матрицы

 - коэффициенты жесткости упругих опор, установленных в сечения ;  - внешние сосредоточенные нагрузки в сечении  ; 

 - радиус параллельного круга при .

В результате прямой ортогональной прогонки получаем матрицу решений

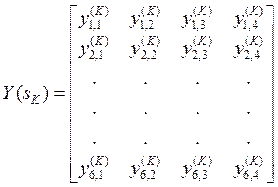                                             (3.10)

для торца  рассматриваемой оболочечной конструкции, а также матрицы

Здесь 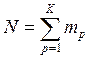;      - общее число оболочечных элементов.

3.3. Определение постоянных интегрирования

В соответствии с граничными условиями (2.3) на торце  оболочечной конструкции формируем расширенную матрицу  системы линейных алгебраических уравнений, которая служит для определения постоянных интегрирования задачи. Например, для случая жесткого защемления торца   эта матраца имеет вид

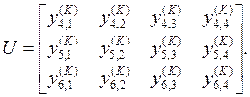                                                   (3.11)

Выполнив решение системы линейных алгебраических уравнений с расширенной матрицей ,  находим постоянные интегрирования ,, для последнего, N-го, участка ортогонализации рассматриваемой составной оболочечной конструкции. Постоянные интегрирования для остальных участков ортогонализации определяем  по рекуррентным формулам:

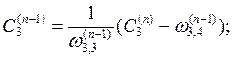
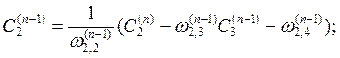                                                  (3.12)

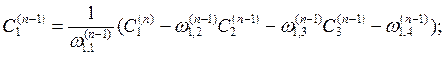
где  - элемент матрацы  для -й точки ортонормирования.

3.4. Обратная прогонка

Векторы решения в точках ортонормирования последнего, N-го, участка ортогонализации определяем  по формуле

                                   (3.13)

где  - векторы-столбцы матрицы решений  в точках  ортонормирования N-го участка ортогонализации.

Определяя затем постоянные интегрирования для (N-1)-го участка ортогонализации по формулам (3.12), находим вектора решения в точках ортонормирования этого участка:

                             (3.14)

где  - векторы-столбцы матрицы решений  в точках ортонормирования (N-1)-го участка ортогонализации.

Переходя далее последовательно к (N-2)-му, (N-3)-му, … , второму, первому участкам ортогонализации, получаем в результате обратной прогонки векторы решения для всех точек ортонормирования рассматриваемой оболочечной конструкции. Недостающие компоненты напряжённо-деформированного состояния конструкции определяем по формулам (2.4) - (2.9).

Изложенной алгоритм является основой для создания программного обеспечения автоматизированного расчета составных оболочечных конструкций на ЭВМ.