Численный анализ напряженно-деформированного состояния составных оболочечных конструкций: Методические указания, страница 2

-  параллели, на которых установлены упругие опоры.

Например, конструкция, представленная на рис.1.1, состоит из 13 оболочечных элементов (номера элементов указаны в кружках) и содержит 14  узловых элементов (пронумерованы на схеме от  0 до 13).

Решение задачи о расчёте напряжённо-деформированного состояния рассматриваемой оболочечной конструкции строим на основе линейной теории оболочек. Для каждого оболочечного элемента должны быть справедливы гипотезы Кирхгофа-Лява.

2. Основные соотношения осесимметричной

задачи термоупругости для оболочек вращения

Напряженно-деформированное состояние замкнутой в окружном направлении оболочки, нагруженной системой внешних осесимметричных нагрузок и осесимметрично нагретой, описывается системой дифференциальных уравнений:

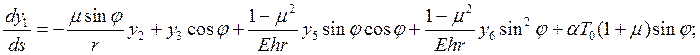
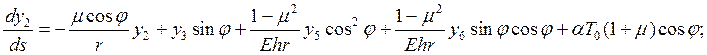
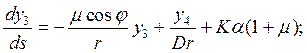                                             (2.1)

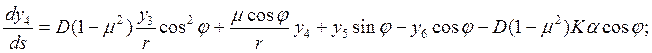
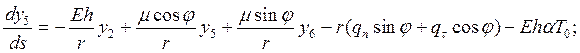
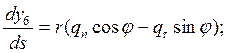
где  - осевое перемещение точек координатной поверхности оболочки;

 - радиальное перемещение точек координатной поверхности оболочки;

 - угол поворота нормали к срединной поверхности оболочки;

                      

 - меридиональный  изгибающий момент;

   - радиальное (распорное) усилие в оболочке;

   - осевое усилие в оболочке;

   - угол между нормалью и осью вращения;

    - радиус параллельного круга;     

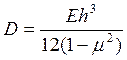    - цилиндрическая жёсткость;

Положительные направления внутренних усилий в оболочке и перемещений показаны на рис. 2.1.

Система дифференциальных уравнений (2.1) должна удовлетворять граничным условиям

                                                     (2.2)

на торце S=0  оболочечной конструкции и граничным условиям

                                            (2.3) на торце . Здесь  если заданы кинематические граничные условия и  если заданы статические граничные условия. Набор шести величин      полностью определяет однородные граничные условия на торцах рассматриваемой конструкции.

Для корректной постановки задачи необходимо, по крайней мере, один узловой элемент конструкции закрепить в осевом направлении. При этом на торцы конструкции могут быть наложены как жесткие, так и упругие связи; на остальные узловые элементы конструкции - только упругие связи,

Решение линейной краевой задачи (2.1)- (2.3) позволяет полностью определить напряженно-деформированное состояние симметрично нагруженной и нагретой составной оболочечной конструкции.

Через компоненты   вектора состояния        (T - индекс транспонирования) выражаются все остальные компоненты напряженно-деформированного состояния оболочечной конструкции:

§  нормальное меридиональное усилие

                                                                  

§  поперечное усилие

                                                                  

 

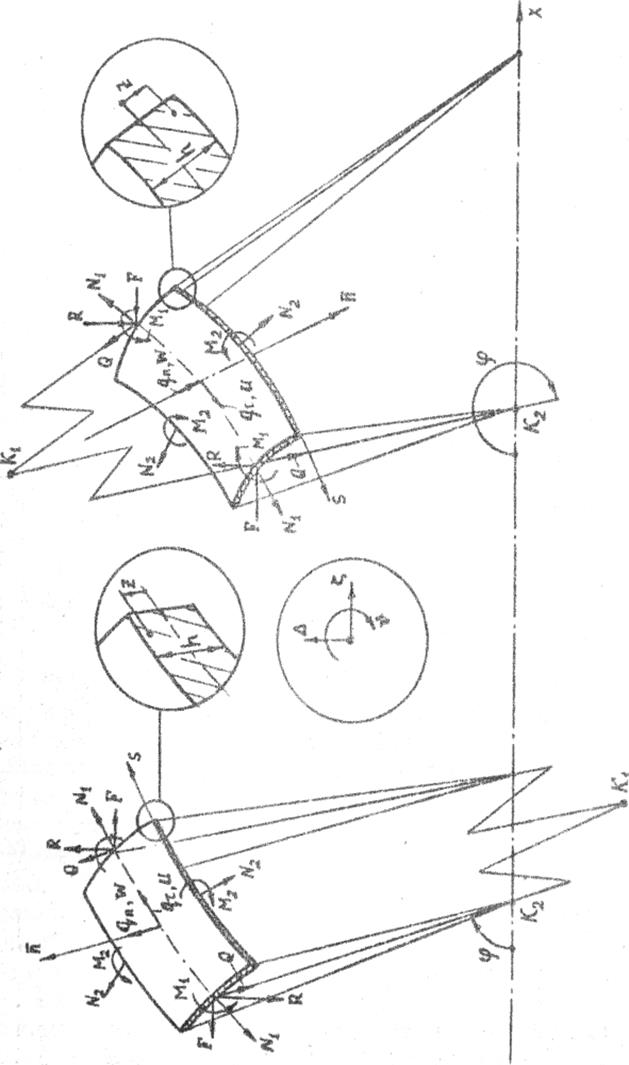Рис.  2.1. Внутренние усилия и перемещения в оболочке

§  нормальное окружное усилие

                                                               

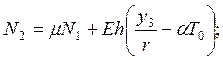
§  окружной изгибающий момент

                                                        

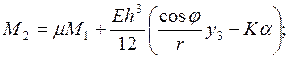
Меридиональные и окружные напряжения в точке, отстоящей на расстояния  z от срединной поверхности (рис. 2.1), определяют по формулам:

                                                                     

                                                                    

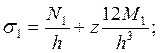
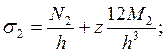
3. Алгоритм численного расчёта напряжённо-деформированного

состояния составной оболочечной конструкции

Решение линейной краевой задачи (2.1) - (2.3) предусматривает выполнение следующих операций.

3.1. Формирование матрицы начальных условий

В общем случае матрицу начальных условий формируем в соответствии с граничными условиями (2.2) на торце  следующим образом:

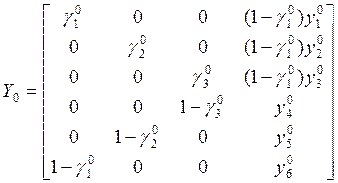                                         (3.1)

Величины  а также  или   полагаем заданными.

В частном случае жесткого защемления торца оболочки  полагаем

Если начальный торец оболочечной конструкции свободен, принимаем     

3.2. Прямая ортогональная прогонка

Систему дифференциальных уравнений (2.1) можно представить в виде

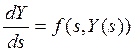,                                                          (3.2)

где  - матрица решений; - решения однородной системы дифференциальных уравнений, соответствующей системе (2,1) при начальных условиях , определяемых первыми тремя столбцами начальной матрицы (3.1);  - решение неоднородной системы уравнений (2.1) при начальных условиях , определяемых четвертым столбцом матрицы .

Каждый оболочечный элемент p рассматриваемой конструкции делим на  участков ортогонализации точками ортонормирования, равномерно расположенными на дуге меридиана. Интегрирование системы уравнений (3.2) на каждом участке ортогонализации p-го оболочечного элемента выполняем методом Рунге-Кутта. В соответствии с этим методом задаем шаг интегрирования ;   решение в узловой точке  выражаем через решение в узловой точке  по формуле