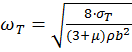Расчет вращающегося диска. Напряженно-деформированное состояние при упругом нагружении материала, страница 2

                                                                                                         (9)

Для диска с центральным отверстием наиболее опасным является окружное сечение  внутреннего контура. Напряженное состояние – одноосное, т.к. , тогда окружное напряжение:

 

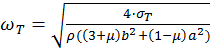                                                                                         (10)

При  в диске возникает кольцевая область пластической деформации материала, примыкающая к внутреннему контуру диска.

Для определения зависимости радиуса границы разделяющ. упругую и пластическую области от угловой скорости можно использовать более простое условие теории наибольших касательных напряжений (условия Треска и Сен-Венана). Максимальное касательное напряжение возникает на площадках равнонаклоненных к площадкам наибольших и наименьших напряжений.

При одноосном растяжении пластические деформации начнутся  

Кроме того, начало пластической сдвигов соответствует условию

Из полученных двух равенств , поэтому для сложного напряженного состояния условия начальной пластичности деформации имеет вид:

При оценке запаса прочности необходимо знать величину предельной угловой скорости  когда пластическая область охватывает весь диск и несущая способность диска полностью исчерпывается.

1.  Рассмотрим сплошной диск постоянной толщины. Решение можно получить методами теории размерности. В случае использования расчетной схемы идеально пластичного конструкционного материала, величина  определяется параметрами: . Из этих величин можно образовать единственную безразмерную комбинацию.

 

2.  Для диска с отверстием пред. угловая скорость зависит еще от одного параметра:

Ее значение определим используя уравнение (2), когда функция

 

 

 

 

 

 

 

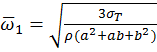                                                                                                     (11)

Для диска без отверстия при

Если исходить из теории МУПД, то для этого случая значения  отличается мало (с=1,79). Поскольку значение  (9) вычисляется так же в соответствии с теорией наибольших касательных напряжений можно сравнить значения  для сплошного диска

 

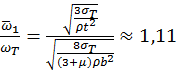
Рассмотрим равновесие половины равномерно нагретого диска переменной толщины без внешних нагрузок на контуре (рис.4)

Рисунок 4 в приложении

а) окружное напряжение б) сечение диска в) диаграмма Прандтля

Инерционные нагрузки дают проекцию отрывающей силы на вертикаль

Обозначим  

 , где r– площадь, J – момент инерции радиального сечения днища

Отрывающее усилие уравновеш. внутр. Напряжениями в диаметральном сечении, которое действует на площадь равную 2F.

Условие равновесия имеет вид:

                                                                                                           (12)

Отсюда получим

 

Из этой формулы следует, что для повышения прочности диска надо увеличить толщину в области ступицы, т.к. при этом момент инерции сечения возрастает медленнее, чем его площадь и значение  увеличивается. Нагрузки на внешнем контуре площади поверхности S пропорциональном , а именно , где λ – коэффициент пропорциональности. В этом случае уравнение равновесия содержит еще одну состовляющую проекции сил на вертикаль.

 

Напряжение на внутреннем контуре (r=a) можно пренебречь, т.к. после радиальных перемещений на внутреннем контуре диска они исчезнут. Таким образом, если диск постоянного сечения при внешнем радиусе b насажен с натягом на жесткий вал радиуса a, так что нормальное давление между валом и диском равно P, то условие скорости при которой диск свободно перемещается относительно вала.

 

Это решение приведено на основании формул (4-7). Для упругого нагружения  поэтому при

Обозначив  и учитывая, что при неравномерном нагреве диска получим из уравнения (12)

                                                                                                      (13)

При постоянной  получим значения предельной угловой скорости для диска постоянной толщины по формуле (11).