Задачи к экзаменационным билетам
1.1. Случайная
функция ![]() задана
в виде
задана
в виде ![]() ,
где
,
где ![]() -
независимые с.в. непрерывного типа с плотностями распределений вероятностей
-
независимые с.в. непрерывного типа с плотностями распределений вероятностей ![]() соответственно.
Найти одномерное распределение СП
соответственно.
Найти одномерное распределение СП ![]() ,
, ![]() ,
, ![]() .
.
1.2. ![]() ,
, ![]() ,
и с.в.
,
и с.в. ![]() .
Найти одномерную функцию распределения и одномерную плотность процесса
.
Найти одномерную функцию распределения и одномерную плотность процесса ![]() .
.
1.3. Найти
одномерную функцию распределения пуассоновского процесса ![]() с
параметром
с
параметром ![]() и
вероятность того, что за время
и
вероятность того, что за время ![]() произойдет четное число скачков.
произойдет четное число скачков.
1.4. Дана
ковариационная функция СП ![]() ,
, 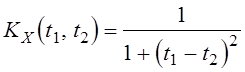 .
Найти
.
Найти ![]() ,
, ![]() , если
, если ![]() .
.
1.5. СП ![]() задан в
виде
задан в
виде ![]() , где
, где ![]() -
неслучайная функция,
-
неслучайная функция, ![]() - с.в. непрерывного типа с плотностью вероятностей
- с.в. непрерывного типа с плотностью вероятностей ![]() . Записать
выражения для
. Записать
выражения для ![]() ,
, ![]() .
.
1.6. Найти
одномерную плотность распределения, МО и дисперсию случайного гармонического колебания
![]() с
постоянной амплитудой
с
постоянной амплитудой ![]() и частотой
и частотой ![]() и случайной фазой
и случайной фазой ![]() , равномерно распределенной на отрезке
, равномерно распределенной на отрезке ![]() .
.
1.7. Случайное
гармоническое колебание задано в виде ![]() , где
, где ![]() - неслучайная частота, а случайные амплитуды
- неслучайная частота, а случайные амплитуды ![]() и
и ![]() независимы
и подчиняются каждая закону распределения
независимы
и подчиняются каждая закону распределения ![]() . Найти одномерную и двумерную плотности процесса.
. Найти одномерную и двумерную плотности процесса.
1.8. СП ![]() есть
величина интервала времени между двумя последовательными скачками пуассоновского
процесса
есть
величина интервала времени между двумя последовательными скачками пуассоновского
процесса ![]() с
параметром
с
параметром ![]() .
Найти одномерную плотность процесса
.
Найти одномерную плотность процесса ![]() .
.
1.9. Угол крена
корабля представляет собой нормальный СП ![]() ,
, ![]() ,
, ![]() .
Известно, что в момент времени
.
Известно, что в момент времени ![]() угол крена корабля составляет
угол крена корабля составляет ![]() . Какова
вероятность того, что в момент
. Какова
вероятность того, что в момент ![]() угол крена корабля будет больше, чем
угол крена корабля будет больше, чем ![]() градусов?
градусов?
1.10. Пусть ![]() - скалярные
с.в. с числовыми характеристиками
- скалярные
с.в. с числовыми характеристиками ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Определить
МО и ковариационную функцию СП
. Определить
МО и ковариационную функцию СП ![]() ,
, ![]() ,
, ![]() ,
постоянна.
,
постоянна.
1.11. Постройте
семейство реализаций СП 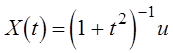 ,
, ![]() ,
, ![]() - скалярная
с. в., распределенная по закону Пуассона с параметром
- скалярная
с. в., распределенная по закону Пуассона с параметром ![]() . Найти МО и
дисперсию СП.
. Найти МО и
дисперсию СП.
1.12. Пусть
известны числовые характеристики двумерного случайного вектора 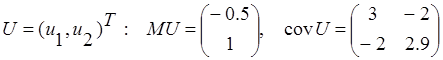 . Найдите МО
дисперсию и ковариационную функцию СП
. Найдите МО
дисперсию и ковариационную функцию СП ![]() .
.
1.13. Найти МО,
дисперсию и ковариационную функцию и одномерный закон распределения СП ![]() ,
, ![]() -
независимые скалярные с.в., распределенные по нормальному закону с нулевым МО и
дисперсией
-
независимые скалярные с.в., распределенные по нормальному закону с нулевым МО и
дисперсией ![]() .
.
2.1. Докажите, что из стационарности в узком смысле следует стационарность в широком смысле.
2.2. Является ли винеровский процесс гауссовским? Марковским?
2.3. Докажите, что пуассоновский процесс является Марковским.
2.4. Определите ![]() - мерный
закон распределения пуассоновского процесса.
- мерный
закон распределения пуассоновского процесса.
2.5. Является ли
скалярный процесс ![]() , где
, где ![]() и
и
![]() - некоррелированные
с.в. с нулевыми математическими ожиданиями и одинаковой дисперсией, равной
- некоррелированные
с.в. с нулевыми математическими ожиданиями и одинаковой дисперсией, равной ![]() ,
стационарным а) в узком смысле? б) в широком смысле?
,
стационарным а) в узком смысле? б) в широком смысле?
2.6. Решить
задачу 2.5., если известна совместная функция плотности вероятностей с.в. ![]() и
и ![]() :
:
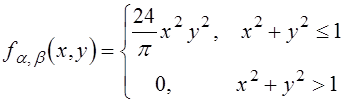 .
.
2.7. Является ли
СП ![]() , стационарным
в широком смысле, если
, стационарным
в широком смысле, если ![]() - стационарный СП и а) для любого фиксированного
- стационарный СП и а) для любого фиксированного ![]() случайные
векторы
случайные
векторы ![]() и
и
![]() являются
независимыми; б)
являются
независимыми; б) ![]() .
.
2.8. Пусть ![]() - скалярный
нормальный стационарный в узком смысле СП. Найдите одномерную и двумерную
функции плотности вероятностей этого СП.
- скалярный
нормальный стационарный в узком смысле СП. Найдите одномерную и двумерную
функции плотности вероятностей этого СП.
2.9. Пусть ![]() -
пуассоновский стационарный скалярный СП с нулевым МО и известной ковариационной
функцией
-
пуассоновский стационарный скалярный СП с нулевым МО и известной ковариационной
функцией ![]() .
Определите МО СП
.
Определите МО СП 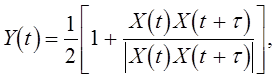 считая
считая ![]() параметром.
параметром.
2.10. Пусть ![]() ,
, ![]() -
винеровский СП, выходящий из нуля и имеющий единичный коэффициент диффузии.
Докажите, что
-
винеровский СП, выходящий из нуля и имеющий единичный коэффициент диффузии.
Докажите, что 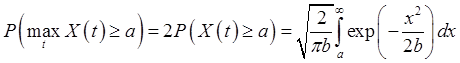 .
.
2.11. СП ![]() является случайным
гармоническим колебанием:
является случайным
гармоническим колебанием: ![]() , где
, где ![]() - случайная амплитуда с плотностью
распределения вероятностей
- случайная амплитуда с плотностью
распределения вероятностей ![]() (равна нулю при
(равна нулю при ![]() ) такая, что существует второй начальный
момент
) такая, что существует второй начальный
момент ![]() ,
, ![]() -
независимая от
-
независимая от ![]() случайная фаза, распределенная
равномерно на отрезке
случайная фаза, распределенная
равномерно на отрезке ![]() . Является ли данный процесс
стационарным в широком смысле?
. Является ли данный процесс
стационарным в широком смысле?
2.12. Показать, что если ![]() -
нормальный стационарный в широком смысле дифференцируемый СП, то процесс
-
нормальный стационарный в широком смысле дифференцируемый СП, то процесс ![]() также нормальный стационарный в широком смысле.
Найти
также нормальный стационарный в широком смысле.
Найти ![]() , если
, если 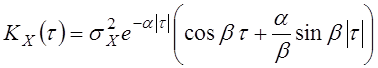 .
.
3.1. Можно ли утверждать, что предел с.ф. обладает обычными свойствами предела неслучайной функции?
3.2. Можно ли утверждать, что предел последовательности с.в. обладает обычными свойствами предела последовательности?
3.3. Доказать, что линейная комбинация и произведение СК непрерывных на Т скалярных СП – СК непрерывные на Т скалярные СП.
3.4. Пусть ![]() -
некоррелированные с.в. и
-
некоррелированные с.в. и 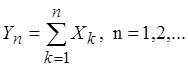 Доказать, что последовательность
с.в.
Доказать, что последовательность
с.в. ![]() сходится
тогда и только тогда, когда одновременно сходятся числовые ряды
сходится
тогда и только тогда, когда одновременно сходятся числовые ряды 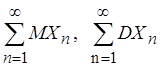 .
.
3.5. Пусть ![]()
![]() скалярные СП, причем
скалярные СП, причем
![]() . Доказать, что
. Доказать, что ![]()
3.6. Пусть ![]() - двумерный
винеровский процесс, выходящий
из нуля. Пусть
- двумерный
винеровский процесс, выходящий
из нуля. Пусть ![]() .
Доказать, что существует
.
Доказать, что существует 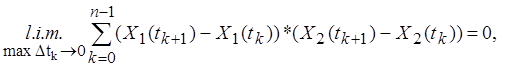 где
где ![]() .
.
3.7. Будет ли СК дифференцируемым на Т случайный процесс
![]() - с.в. распределенная равномерно на отрезке
- с.в. распределенная равномерно на отрезке ![]() .
. ![]()
3.8. Пусть ![]() - с.в.,
распределенная по равномерному
закону на отрезке
- с.в.,
распределенная по равномерному
закону на отрезке ![]() . Является ли:
. Является ли:
а)
СП ![]() , СК
дифференцируемым?
, СК
дифференцируемым?
б)
произвольная реализация СП ![]() , дифференцируемой?
, дифференцируемой?
3.9. Пусть ![]() , где
, где ![]() -
некоррелированные с.в.
с нулевыми математическими ожиданиями и одинаковыми дисперсиями, равными 0,1.
Найти МО, дисперсию и ковариационную функцию СП
-
некоррелированные с.в.
с нулевыми математическими ожиданиями и одинаковыми дисперсиями, равными 0,1.
Найти МО, дисперсию и ковариационную функцию СП ![]() .
.
3.10. Найти ![]() , если
, если ![]() ,
, ![]() ,
, ![]() ,
, 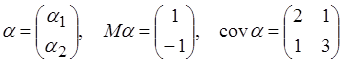 .
.
3.11. СК
дифференцируемый СП ![]() , имеет МО
, имеет МО ![]() и ковариационную функцию
и ковариационную функцию ![]() . Найти МО и ковариационную функцию СП
. Найти МО и ковариационную функцию СП ![]() .
.
3.12. Пусть ![]() -
стационарный в широком смысле СП, дифференцируемый на Т.
-
стационарный в широком смысле СП, дифференцируемый на Т.
3.13. Является
ли стационарным в широком смысле СП ![]() ?
?
3.14. Доказать, что производная гауссовского процесса - гауссовский процесс.
3.15. Пусть ![]() , -
стационарный в широком смысле СП с ковариационной функцией
, -
стационарный в широком смысле СП с ковариационной функцией
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.