Дифференциальные формы. Уравнения Максвелла.

Дифференциальные формы (уравнения Максвелла)

Как правило, законы физики описывают с использованием классического векторного исчисления. Эти законы как мы уже рассматривали, можно описать, использую альтернативный аппарат, а именно дифференциальные формы.

Они активно применяются в теоретической физике, но ещё не так активно используются математиками-прикладниками и инженерами.

Язык дифференциальных форм позволяет выражать законы физики независимо от любой конкретной координатной системы. Как правило, векторные конечные элементы пользуются дифференциальными формами очень активно. Представляет интерес: показать связь между векторными конечными элементами и дифференциальными формами.

Дифференциальные формы выражаются посредством процедур интегрирования. Форма степени p, или p-форма, есть выражение, которое появляется в p-кратных интегралах по области. Например, работа по перемещению единичного заряда электрическим полем определяется соотношением:

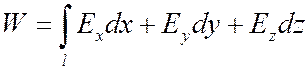 - где величина подынтегрального выражения (интеграл по линии - линейный) есть 1-форма . Или полный ток, текущий через поверхность дается соотношением:

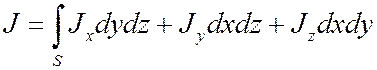 - подынтегральное выражение в поверхностном интеграле есть 2-форма J. А полный заряд в объеме есть:

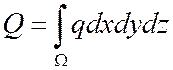 - где подынтегральное выражение есть 3-форма. Скалярные функции ни положения в пространстве, также как электростатический потенциал , есть нуль-форма. Его интегрируют по области размерности нуль, т.е. по точке .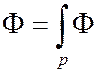

Дифференциальная форма есть обобщение традиционной векторной алгебры и векторных исчислений. Градиент, дивергенция и ротор  векторных исчислений заменяются одним дифференциальным оператором d, называемым внешней производной. Аналогично скалярное произведение и векторное произведение заменяются единственным внешним произведением. Термин «внешний» используется потому, что производная от p–формы не есть p–форма, она лежит вне (следовательно, внешняя) пространства p –форм. Аналогично, произведение двух p–форм не есть p–форма.

Уравнения Максвелла, выписанные с использованием аппарата дифференциальных форм, имеют вид:

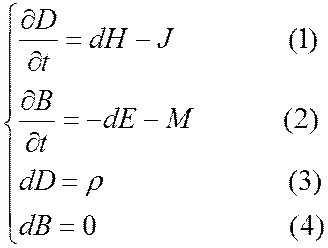                        (ı)

В (ı) -  D – плотность электрического потока (индукции), B – плотность магнитного потока – суть 2- формы; напряженность электрического(E) и магнитного(H) полей – суть 1-форма; плотность токов электрического(J) и магнитного(M) – это 2-формы; и плотность (объемная) электрического заряда    есть 3-форма.

Для простоты будем полагать проводимость (электрическую) равной нулю. Оператор d является однозначным (ясным), т.к. есть только один путь, чтобы продифференцировать p –форму, а именно, производная от p –формы есть p+1 –форма.

Тогда законы материальные, а именно , таковы, что  – это не простые скаляры, но скорее операторы, которые превращают (обращают) 2 – формы в 1 – формы. Эти операторы определяются метрикой пространства, в котором  (ı) - уравнения  Максвелла, определены таким образом, «мера» электрического поля(E) и магнитного поля(H) есть  и , где произведение определено однозначно, т.к. произведение p – формы и q –формы  есть (p+q)-форма. Следовательно,  и  представляют плотность электрической и магнитной энергии соответственно, которые являются 3 – формами. Умножая (ı.1) на E и (ı.2) на H получим:

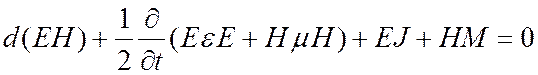         (ıı)

Выражение (ıı) есть теорема Пойнтитс о сохранении энергии. Произведение EH есть 2 – форма, которая представляет поток энергии, 3 – формы EJ и HM представляют плотность энергии, обеспечиваемой источниками.

В трехмерном пространстве есть четыре дифференциальные формы: 0 - форма, 1 – форма, 2 – форма, 3 – форма. Эти формы могут быть ассоциированы с Гильбертовыми пространствами. Связь между дифференциальными формами, Гильбертовыми пространствами, электромагнитными переменными и конечными элементами можно представить в виде таблицы.

	0– форма	1– форма	2– форма	3- форма
Интеграл	Точка	Линия	Поверхность	Объем
Производная	grad	curl	div	Нет
Непрерывность	Полная	Тангенциальная	Нормальная	Нет
Гильбертово пространство	H(grad)	H(curl)	H(div)
Электромагнетизм	Потенциал	Поля(E,H)	Потоки, токи (B,D,J)	Плотность заряда(объемного)
Конечные элементы	V(узловой)	W(edge)	F(face)	S(объем)

Галеркинские формулировки уравнений Максвелла

Используем векторные конечные элементы  и  в качестве базисных функций для электрического поля  и магнитной индукции  соответственно.

Пусть – базисная функция, ассоциированная с ребром i и – базисная функция, ассоциированная с гранью i, тогда электрическое поле

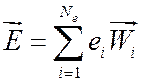, а магнитная индукция  .

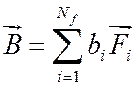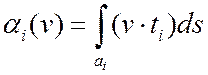В соответствии с определением  ( edge –элементы на тетраэдрах или шестигранниках (кубах)) и их степеней свободы ()  имеют физическую единицу – вольт и могут быть проинтерпретированы как напряжение (разность потенциалов) вдоль ребра i данной сетки. Аналогично определяется и , тогда степени свободы  имеют физическую единицу – вебер и могут быть проинтерпретированы как магнитный поток через грань i. Независимые источники тока(J –электрический, M –магнитный) также можно представить в виде линейной комбинации базисных функций:

;

.

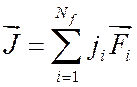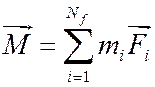Тестовые пространства  и  состоят из edge- и face – элементов для ребер и граней, не принадлежащих границе . Теперь, используя эти допустимое пространство и тестовое пространство, выпишем Галеркинские постановки.

Приведем две формы записи систем уравнений Максвелла: система уравнений 1-го порядка и уравнение второго порядка.  

1.  Уравнения первого порядка:

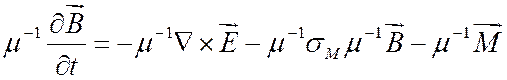,   в ;

,         в ;

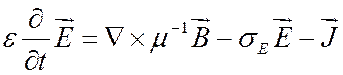,   в ;

,   в ;

  на ;

;

;

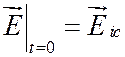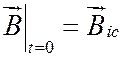2.  Уравнение второго порядка:

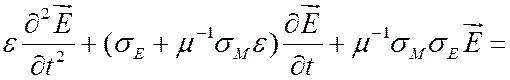
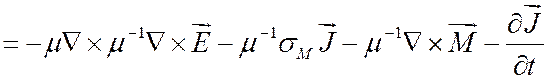,   в ;

,   в ;

  на ;

;

;

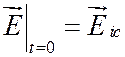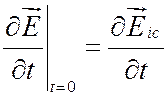Формулировка Галеркина для (1):

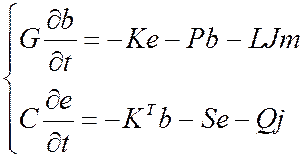                       (**), где

;;

       ;;

;;

.

Представление (**) особенно важно тем, что первое уравнение включает слагаемое с матрицей K, а второе – с матрицей , следовательно дискретные уравнения имеют такую же гиперболичность, что и исходные уравнения Максвелла. Это свойство не присутствует в некоторых других методах, которые используют вариационные формы уравнений Максвелла. Это свойство обеспечивает стабильную, недиссипативную процедуру интегрирования по времени.

Матрицы C и G симметричны и положительно определены, и они могут быть проинтерпретированы как «матрица емкости» и «матрица индуктивности» на сетке соответственно. Матрицы S и P можно интерпретировать как электрическую и магнитную сеточную проводимости (матрица ).

Формулировка Галеркина для (2):

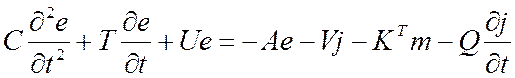, где элементы матриц имеют вид:

,

,

,

.

Можно показать, что матрица , A- положительно определена и симметрична, сохраняется гиперболичность исходной системы уравнений.