




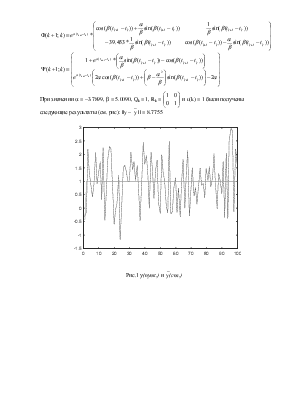
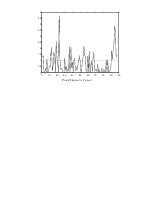


Министерство образования Российской Федерации
Новосибирский государственный технический университет
Кафедра прикладной математики

Индивидуальная работа по
«Теории автоматического управления» на тему
«Адаптивная линейная фильтрация при параметрической априорной неопределенности, алгоритм с оцениванием R(k+1)»
Факультет: ПМИ
Студенты: Большакова А. В.
Журавлев В. А.
Миркин Е. П.
Группа: ПМ – 83
Преподаватель: Карманов В. С.
2001 г.
Задача адаптивной фильтрации при параметрической неопределенности возникает в результате частичной априорной статистической неопределенности, при которой закон распределения компонент, оцениваемых и проверяемых компонентов известен с точностью до некоторой совокупности параметров. Параметрически адаптивный алгоритм оценивания – алгоритм, котороый на основе обработки измерительной информации способен не только давать оценку требуемых компонент случайных процессов, но и восстанавливать статистические характеристики априорного описания динамической системы и измерений.
1. Модель системы описывается рекурентным соотношением
![]() (1), где х(k) – вектор
состояния системы, u(k) – вектор
управления, w(k)
– вектор возмущений, Ф(k+1, k) – переходная матрица состояния
системы, Y(k+1, k) – матрица управления, Г(k+1,k) – матрица возмущения.
(1), где х(k) – вектор
состояния системы, u(k) – вектор
управления, w(k)
– вектор возмущений, Ф(k+1, k) – переходная матрица состояния
системы, Y(k+1, k) – матрица управления, Г(k+1,k) – матрица возмущения.
2. Модель дискретных измерений
![]() (2), где Нк –
матрица измерений, v(k) – вектор
возмущений
(2), где Нк –
матрица измерений, v(k) – вектор
возмущений
3. Априорные данные:
x(0) ~ N(x(0), P0), w(k) ~ N(0, Qk), v(k) ~ N(0, Rk);
cov(w(k), w(j)) = Qk*dij; cov(v(k), v(j)) = Rk*dij; (3)
cov(w(k), v(j)) = cov(x(0), w(k)) = cov(x(0), v(k)) = 0;
1. Алгоритм экстраполяции значений x(k+1,k) = M(x(k+1)|![]() ) и P(k+1,k)=cov(x(k+1),x(k+1)|
) и P(k+1,k)=cov(x(k+1),x(k+1)| ![]() ) имеет вид:
) имеет вид:
x(k+1,k) = Ф(k+1,k)*x(k,k) + Y(k+1,k)*u(k) (4),
P(k+1,k) = Ф(k+1,k)*P(k,k)*ФT(k+1,k) + Г(k+1,k)*Qk(k,k)*ГT(k+1,k) (5)
2. Алгоритм фильтрации значений x(k+1,k) = M(x(k+1)|![]() ) и P(k+1,k)=cov(x(k+1),x(k+1)|
) и P(k+1,k)=cov(x(k+1),x(k+1)| ![]() ) задается рекурентным соотношением:
) задается рекурентным соотношением:
x(k,k) = x(k,k–1) + Kk(y(k)–Hk*x(k,k–1)); (6),
Kk
= P(k,k–1)*![]() [Hk*P(k,k–1)*
[Hk*P(k,k–1)* ![]() + Rk]–1; (7),
+ Rk]–1; (7),
P(k,k) = (E – Kk*Hk)*P(k,k–1) (8).
Алгоритм с оцениванием матрицы Rk
В отличие от фильтра Калмана, информация о точном значении матрицы Rk не доступна. То есть необходимо внести в алгоритм изменения с целью оценить матрицу Rk каким-либо образом. Для оценки матрицы Rk введем дополнительную величину – матрицу Ck, связанную с Rk соотношением
Ck
= Hk*P(k,k–1)*![]() + Rk, которую мы и будем в
дальнейшем оценивать вместо матрицы Rk.
+ Rk, которую мы и будем в
дальнейшем оценивать вместо матрицы Rk.
![]() = (y(k) – Hk*-x(k,k–1))*(y(k) –
Hk*x(k,k–1))T
= (y(k) – Hk*-x(k,k–1))*(y(k) –
Hk*x(k,k–1))T
С учетом вышеизложенных изменений в алгоритме произойдут некоторые изменения.
Пусть модели состояния и наблюдения описываются разностными уравнениями (9) и (10) сответственно:
![]() (9),
(9),
![]() (10).
(10).
Априорные данные:
x(0) ~ N(x(0), P0), w(k) ~ N(0, Qk), v(k) ~ N(0, Rk);
cov(w(k), w(j)) = Qk*dij; cov(v(k), v(j)) = Rk*dij; (11)
cov(w(k), v(j)) = cov(x(0), w(k)) = cov(x(0), v(k)) = 0;
где матрицы Р0, Qk – известны заранее, матрица Rk – неизвестна.
Пусть критерий оптимизации имеет вид:
![]()
![]() (12)
(12)
Здесь под ![]() понимается совместная условная плотность
распределения х(k) и у(k).
понимается совместная условная плотность
распределения х(k) и у(k).
Тогда
1. Алгоритм экстраполяции значений:
x(k+1,k)
= M(x(k+1)|![]() ) (13)
) (13)
P(k+1,k)=cov(x(k+1),x(k+1)|
![]() ) (14)
) (14)
имеет вид:
x(k+1;k) = Ф(k+1,k)*x(k;k) + Y(k+1,k)*u(k) (15)
P(k+1;k) = Ф(k+1,k)*P(k;k)* ФT(k+1,k) + Г(k+1,k)*Qk*ГT(k+1,k) (16)
2.
Алгоритм
фильтрации значений x(k+1,k) = M(x(k+1)|![]() ) и
) и
P(k+1,k)=cov(x(k+1),x(k+1)|
![]() ) задается рекурентными соотношениями:
) задается рекурентными соотношениями:
v(k) = y(k) – Hk*x(k;k–1) (17)
![]() = v(k)*v(k)T (18)
= v(k)*v(k)T (18)
Kk = P(k;k–1)*![]() *
*![]() (19)
(19)
x(k;k) = x(k;k–1) + Kkv(k) (20)
P(k;k) = P(k;k–1) – Kk*![]() *
*![]() (21)
(21)
Доказательство.
ln![]() = ln
= ln ![]() + ln
+ ln ![]() =
=
= ln![]() + ln
+ ln![]() , т.е. формулу (12) перепишем в виде
составного критерия:
, т.е. формулу (12) перепишем в виде
составного критерия:
![]() ln
ln![]() (22)
(22)
![]() ln
ln
![]() (23)
(23)
Справедливость того, что в силу критерия (22), модели состояния (9) и модели наблюдения (10), алгоритм экстраполяции задается соотношениями (15),(16), следует из дискретного фильтра Калмана. Покажем, что алгоритм фильтрации соответствует критерию (23). Т.к. в критерии (22) и (23) входит неизвестная величина Rk, необходимо найти ее оценку, используя соотношение (23).
Используя (11), можно записать
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.