Адаптивная линейная фильтрация при параметрической априорной неопределенности, алгоритм с оцениванием R(k+1), страница 2

ln= ln2p – ln|cov(y(k),y(k)|,Rk)| – n(k)T(cov(y(k),y(k)|,Rk))–1n(k)

(24)

где n(k) = y(k) – M(y(k)|,Rk). Используя (10) и (13), а так же соотношение

M(y(k)| ,Rk) = M(Hk*x(k)|) = Hk*x(k;k–1), представим выражение v(k) в виде:

n(k) = y(k)–Hk*x(k;k–1) = Hk*x(k) + v(k) – Hk*x(k;k–1) = Hk(x(k)–x(k;k–1)) + v(k)      (25)

Т.к. M(n(k)|,Rk) = 0, поэтому из (25) и (14) имеем:

cov(y(k),y(k)|) = M(n(k),n(k)T|,Rk) =

= M(Hk(x(k) – x(k;k–1))*(x(k) – x(k;k–1))T|,Rk) + M(Hk(x(k) – x(k;k–1))*v(k)| ,Rk) +

+ M(v(k)*(x(k)–x(k;k–1))T*|,Rk) + M(v(k)v(k)T|,Rk) = Hk*P(k;k–1)*  + Rk = Ck

(26)

Подставляя (26) в (24), получаем

ln = ln2p – ln|Ck| – n(k)Tn(k) = ln        (27)

Т.о. заменим (23) на ln. Из (27) получим условие существования экстремума

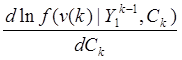 = –  + = 0

т.е. = . Обозначим = .

Определим корреляционную матрицу Kk* из (26)

M[Kk**|,Rk] = Kk*M[|,Rk]*  = Kk*Ck*.

Используем (7) и симметричность матриц Ck и P(k;k–1):

Kk*Ck* = Kk*Ck*()T*Hk*P(k;k–1) = Kk*Hk*P(k;k–1)

Т.о. из (8)

P(k;k) = P(k;k–1) – Kk*Hk*P(k;k–1) = P(k;k–1) – Kk*Ck*

где, заменив Ck на , получим (21).

■

Тестирование

Тестирование проводилось на основе системы управления космическим кораблем по одной координате. Параметры модели имеют вид:

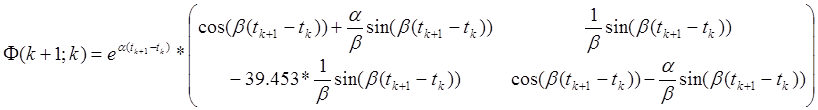
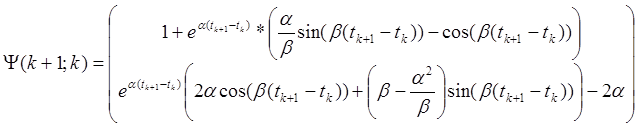
При значении a = –3.7899, b = 5.0090, Qk = 1, Rk = 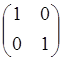 и u(k) = 1 были получены следующие результаты (см. рис): ||y –`y || = 8.7755

 


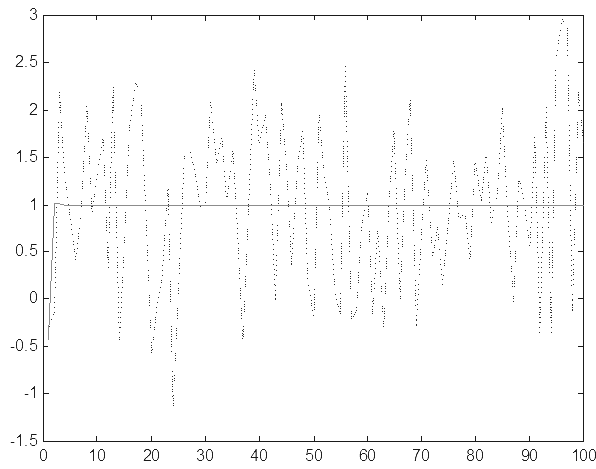Рис.1 у(пунк.) и`y(спл.)


 


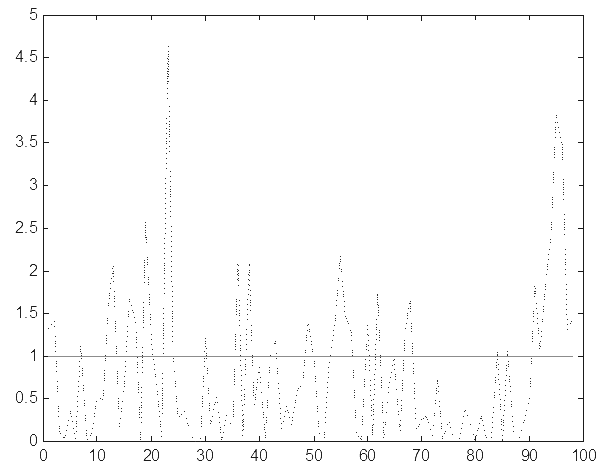Рис.2 С(пунк.) и`С(спл.)

Приложение 1

Текст программы в системе MATLAB

syms tau; syms tkp; syms tk;

Kr=3.17e5; Kp=1.65e6; Jv=4.1822e4;

F=[-Kr/Jv, 1; -Kp/Jv, 0]; C=[0;Kp/Jv]; //Инициализация

H=[1,0]; u=ones(1,1); Q=eye(size(u,1)); R=eye(2);

//Н - строка, u=1, Q=1, R – единичная матрица 2х2

P=eye(2);              // Р – единичная матрица 2х2

G=(zeros(1,2))';        // G – нулевой столбец

realx=zeros(2,steps);   // realx – матрица 2хsteps

Psi_sym=int(expm(F*(tkp-tau))*C,tau,tk,tkp); // Psi_sim =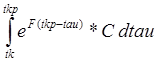

Gamma_sym=int(expm(F*(tkp-tau))*G,tau,tk,tkp); // Gamma_sym =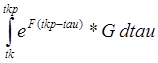

// генерация выборки

realx(:,1)=(normrnd(0,P(1,1),1,size(realx,1)))';

// В первый столбец заносится случайная величина, имеющая нормальное распределение с мат. ожиданием 0 и дисперсией Р(1,1).

y=zeros(1,size(realx',1)); // у – строка размера steps

v=normrnd(0,R(1,1),1,size(y,1));

//v-случайная величина, имеющая нормальное распределение с мат. ожиданием 0 и дисперсией R(1,1).

y(:,1)=H*realx(:,1)+v';

Phi=expm(F*(1));             // Phi =

for i=2:size(realx',1)       // Цикл по i от 2 до steps

tkp=i+1;

tk=i;

Psi=eval(Psi_sym);        // Вычислить выражение для Psi_sym

Gamma=eval(Gamma_sym);       // Вычислить выражение для Gamma_sym

w=normrnd(0,Q(1,1),1,size(G',1));

// Сформировать СВ, имеющую нормальное распределение с мат. ожидание 0 и дисперсией Q(1,1).

realx(:,i)=Phi*realx(:,i-1)+Psi*u'+Gamma*w';

// Считаем следующий х через предыдущий.

v=normrnd(0,R(1,1),1,size(y,1));         // Считаем помеху

y(:,i)=H*realx(:,i)+v';                  // Вычисляем отклик (измерение).

end

// алгоритм фильтрации

x=zeros(size(realx,1),size(realx',1));

x(:,1)=realx(:,1);                    // Помещаем в х первый столбец realx

Phi=expm(F*(3-2)); syms tau;

Psi=double(int(expm(F*(3-tau))*C,tau,2,3));     //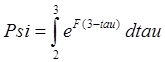

Gamma=double(int(expm(F*(i+1-tau))*G,tau,i,i+1)); //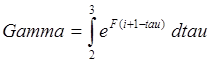

x(:,2)=Psi*u+Phi*x(:,1);        // считаем 2ю компоненту х чере 1ю

P=Phi*P*Phi'+Gamma'*Q*Gamma;      // считаем Р

for i=2:size(realx',1)-1          // цикл от 2 до steps

//фильтрация

nu=y(:,i)-H*x(:,i);            // считаем v

Cn=nu*nu';                        // считаем Cn

An2(1,i-1)=Cn;

An2(2,i-1)=[1,0]*R*[1,0]' + H*P*H';

K=P*H'*pinv(Cn);                  // pinv - псевдообращение

P=P-K*Cn*K';                      // пересчитываем Р

x(:,i)=x(:,i)+K*nu;            // пересчитываем х

// экстраполяция

tkp=i+1;

tk=i;

Psi=eval(Psi_sym);                // вычисляем новое Psi

Gamma=eval(Gamma_sym);           // вычисляем новое Gamma

x(:,i+1)=Psi*u+Phi*x(:,i);        // считаем новый х

P=Phi*P*Phi'+Gamma'*Q*Gamma;      // пересчитываем Р

end

// вывод результатов

i=size(realx',1); nu=y(:,i)-H*x(:,i); Cn=nu*nu'; K=P*H'*pinv(Cn);

P=P-K*Cn*K'; x(:,i)=x(:,i)+K*nu; Cnew(i)=Cn;

y_ap=zeros(1,size(realx',1));

for i=1:size(realx',1)

y_ap(:,i)=H*x(:,i);

end

An1=[y',y_ap'];

II=zeros(1,size(realx',1));

for i=1:size(realx',1)

II(i)=i;

end

plot(II,An1(:,1)',':',II,An1(:,2)','-')

for i=1:size(An2',1)

II2(i)=i;

end

C=An2';

plot(II2,C(:,1),':',II2,C(:,2),'-')

Скачать файл