


































программирования бывает необходимо записывать результаты вычислений в текстовый файл. Это может быть сделано для того, чтобы передать затем эти данные из текстового файла в другое приложение с целью их последующей обработки. Также данные из текстового файла могут быть считаны для последующего их использования в программе. Для подобных операций записи и чтения в Pascal существуют специальные команды. Рассмотрим пример программы, с последующим комментарием.
Program ReadWrite;
Uses crt;
Var a,b:real;
File:text;
Begin
Write(‘Введите число’);
Readln(a);
b:=2*a;
Assign(Fail,’D:\data.txt’);
Rewrite(File);
Writeln(File,‘Ответ: b=’,b:2:3);
Close(File);
End.
При работе с текстовым файлом появляется новая переменная (File) формата text. Перед записью данных устанавливается связь переменной File с конкретным файлом на компьютере с помощью команды Assign. Последующая команда Rewrite перезаписывает указанный файл или создает его заново, если такого нет по указанному пути. При записи в команде вывода Write в начале указывается, что вывод будет осуществляться в переменную File, а, следовательно, в файл data.txt. Работа с файлом заканчивается командой Close.
Дополнительно существует команда Append, которая позволяет добавлять данные в уже имеющийся файл без его перезаписи.
При чтении данных из файла вместо команды Write используется команды Read.
3. ПРИМЕРЫ СОСТАВЛЕНИЯ АЛГОРИТМОВ И ПРОГРАММ
3.1 Линейный алгоритм
Пример 1. Определить мощность главных двигателей судна для обеспечения скорости хода 20 узлов, если известно сопротивление воды движению судна и пропульсивный КПД установки.
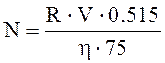 ,
,
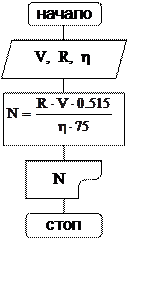 |
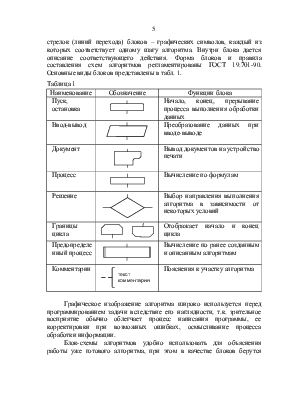
Рисунок 1 – Блок схема линейного алгоритма
Программа:
Program Primer1;
Uses Crt;
Var N,V,R,KPD:real;
Begin
Write(‘Введите сопротивление воды движению судна, кг:’);
Readln(R);
Write(‘Введите скорость хода судна, уз:’);
Readln(V);
Write(‘Введите пропульсивный кпд установки:’);
Readln(KPD);
N:=0.515*R*V/(75*KPD);
Writeln(‘Мощность главных двигателей N=’, N:1:3);
Readkey;
End.
3.2 Разветвляющийся алгоритм

Пример 2. Составить блок-схему алгоритма вычисления угла перекладки руля судна в
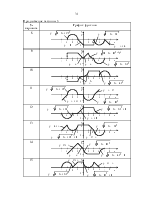
произвольный момент времени. Характер изменения угла перекладки руля изображен
на рис. 2.
Рисунок 2 – Характер изменения угла перекладки руля
Программа:
Program Primer2;
Uses Crt;
Var a1,t,t1,t2,t3:real;
Begin
Write(‘Введите параметр t1:’);
Readln(t1);
Write(‘Введите параметр t2:’);
Readln(t2);
Write(‘Введите параметр t3:’);
Readln(t3);
Write(‘Введите время t:’);
Readln(t);
Write(‘Введите значение угла alfa1, уз:’);
Readln(a1);
If t<t1 then a:=a1*t/t1 else
If t<t2 then a:=a1 else
If t<t3 then a:=a1*(t3-t)/(t3-t2) else a:=0;
Writeln(‘Угол перекладки руля alfa=’, a:1:3);
Readkey;
End.
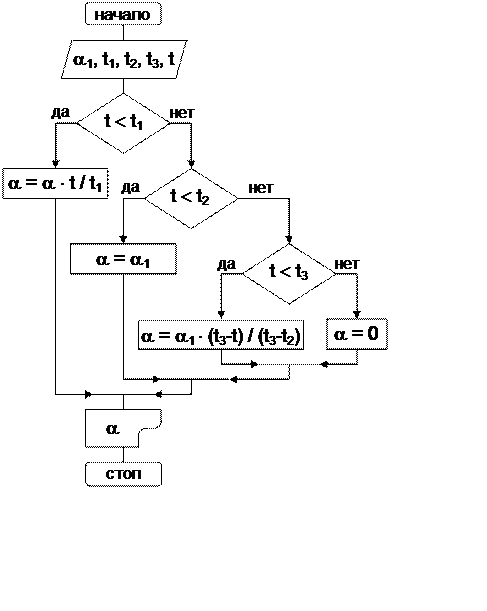 |
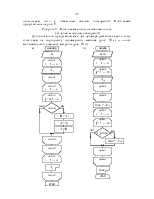
Рисунок 3 – Блок-схема разветвляющегося алгоритма
Дополнительно рассмотрим несколько вариантов написания команды условия в зависимости от вида блок-схемы (рис.4 – рис.6). В данных примерах показаны записи команд от самой краткой до самой полной.
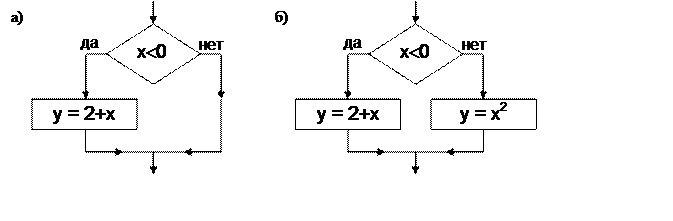
Рисунок 4 – Условие с действиями на одной (а) и
двух ветках (б)
Команда (вариант а):
If x<0 then y:=2+x;
Команда (вариант б):
If x<0 then y:=2+x else y:=sqr(x);
 |
последовательное (а) и вложенное (б)
Команда (вариант а):
If x<0 then y:=2+x;
If x<=2 then y:=sqr(x);
Команда (вариант б):
If x<0 then y:=2+x else
If x<=2 then y:=sqr(x) else y:=x-1;
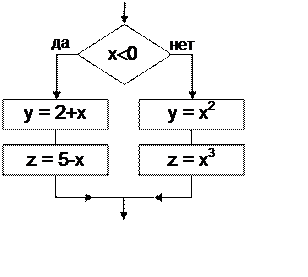 |
Команда:
If x<0 then
begin
y:=2+x;
z:=5-x;
end
else
begin
y:=sqr(x);
z:=x*x*x;
end;
Последняя запись представляет собой полный вариант написания команды условия (см. п.2.5). Парная команда begin-end в команде условия If применяется, когда на какой-либо ветке имеется два и более действия. При этом под действиями подразумеваются не только формулы, но и, например, ввод данных, вывод на экран, циклы, другие условия и т.д.
3.3 Циклический алгоритм
Пример 3. Составить алгоритм решения задачи извлечения квадратного корня из действительного положительного числа, основанный на построении монотонной последовательности, сходящейся к корню.
Для решения задачи используем рекуррентную формулу, т.е. формулу, позволяющую выразить (n+1)-й член последовательности через значение её предыдущего члена по формуле
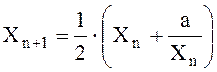 ,
,
Условием окончания процесса является выполнение
неравенства ![]() , где e -характеризует требуемую точность вычислений.
, где e -характеризует требуемую точность вычислений.
Так как число членов последовательности заранее неизвестно, то в данном примере необходимо использовать цикл с неизвестным числом повторений (см. п.2.6). Блок-схема вычисления квадратного корня из действительного числа представлена на рис. 7.
Программа:
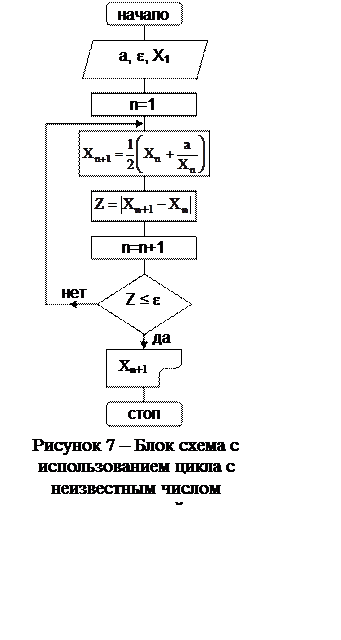 Program
Primer3;
Program
Primer3;
Uses Crt;
Var a,e:real;
X:array [1..100] of real;
Begin
Write(‘Введите число, для которого вычисляется корень:’);
Readln(a);
Write(‘Введите значение первого члена последовательности:’);
Readln(X[1]);
Write(‘Введите величину погрешности:’);
Readln(e);
n:=1;
Repeat
X[n+1]:=0.5*(X[n]+a/X[n]);
Z:=abs(X[n+1]-X[n]);
n:=n+1;
Until Z<=e;
Writeln(’Значение корня заданного числа’,X[n+1]:2:3);
Readkey;
End.
Пример 4. Составить блок-схему алгоритма численного интегрирования определенного интеграла методом трапеций.
Как известно, вычисление определенного интеграла
сводится к вычислению площади криволинейной трапеции, ограниченной функцией f(x), осью абсцисс и прямыми линиями ![]() и
и ![]() (рис. 8) по формуле
(рис. 8) по формуле
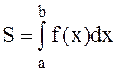
Приближенное значение этой площади легко вычисляется, если
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.