Лабораторная работа № 10. Профилирование эвольвентных зубьев., страница 6

-  посередине профиля зуба – осью симметрии;

-  переход от эвольвенты к окружности впадин осуществляют дугой переходной окружности радиусом = 0,4m.

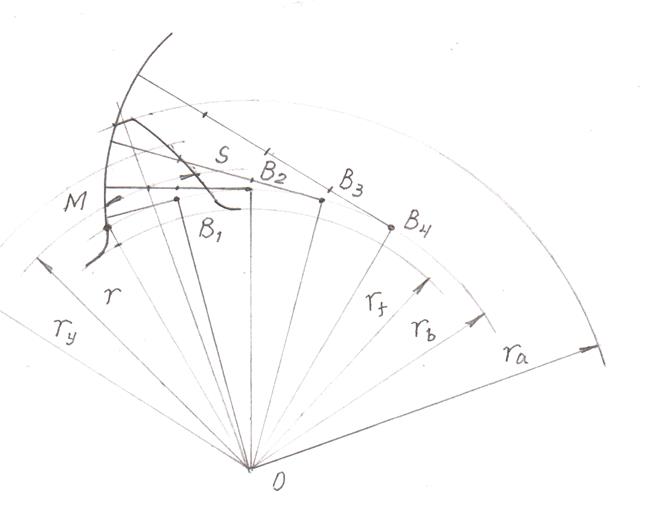
Рис. 10.11

Для определения положения оси симметрии зуба вычерчивают делительную окружность диаметром d – формула (10.6) - и по ней откладывают половину делительной толщины зуба

.

(10.24)

Полученную засечку соединяют с центром О окружностей, получая ось симметрии зуба. Вторую половину профиля получают, вычерчивая симметричный полупрофиль. Для повышения точности эвольвенты вводят дополнительную окружность произвольного радиуса r_y приблизительно посередине между окружностями вершин и делительной, на которой измеряют и откладывают толщину  s_y. Профиль ножки зуба между эвольвентой и окружностью впадин формируется переходной кривой. Ширина впадины между зубьями по делительной окружности:

.                                                       (10.25)

     Пример 10.1. Вычертить в масштабе эвольвенту и профиль одного зуба. Рассчитать d, d_b, d_a, d_f, p, s, e. Угол профиля a = 20⁰. Коэффициент высоты головки зуба  = 1. Коэффициент радиального зазора c* = 0,25. Коэффициент радиуса переходной кривой  = 0,4. Исходные данные: модуль m = 6 мм; число зубьев колеса z = 12; коэффициент смещения x = + 0,5; коэффициент уравнительного смещения Δy = 0,07.

Решение.

         Делительный диаметр d = 6∙12 = 72 мм.

         Основной диаметр d_b = 6∙12∙cos20^˚ = 67,66 мм.

         Диаметр окружности вершин d_a = 6∙(12 + 2 + 2∙0,5 – 2∙0,07) = 89,16 мм.

Диаметр окружности впадин d_f =  6∙(12 – 2,5 + 2∙0,5) = 63 мм.

Делительная толщина зуба s = 0,5∙π∙6 + 2∙0,5∙6∙tg20^˚ = 11,61 мм.

Шаг зубчатого колеса p = π∙ m = π∙6 = 18,85 мм.

Делительная  ширина впадины e = 18,85 – 11,61 = 7,24 мм.

Радиус переходной кривой = 0,4∙6 = 2,4 мм.

Выполняем построения в соответствии с вышеизложенными рекомендациями в масштабе. Графическое решение задачи представлено на рис. 10.11.

Б) Геометрия нулевого зубчатого колеса.

Исходные данные для расчёта геометрии содержат модуль m и число зубьев z, а также параметры нормального исходного контура: α = 20º; ; с^* = 0,25. Рассчитывают следующие геометрические параметры: делительный диаметр d – формула (10.6), основной диаметр d_в – формула (10.8), диаметр окружности вершин при отсутствии смещения:

d_a = m (z + 2);                                                   (10.26)

диаметр окружности впадин:

d_f = m (z – 2,5);                                                   (10.27)

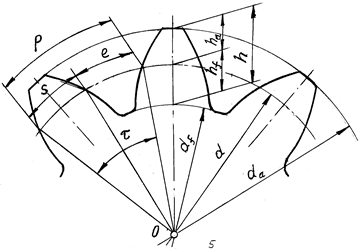
шаг колеса – формула (10.2), делительная толщина зуба – формула (10.1), высота головки зуба, ножки зуба, полная высота зуба:

h_a = m; h_f = 1,25m; h = 2,25m.                                     (10.28)

Геометрические параметры зубчатого колеса показаны на рис. 10.11.

В) Геометрия нулевого равносмещенного зацепления.

В равносмещенном зацеплении число зубьев шестерни  z₁ < 17 и для устранения подрезания ножки зуба требуется выполнить положительное смещение шестерни с коэффициентом х₁, рассчитанным по формуле:

х₁ = (17 - z₁)/17.

Коэффициент смещения колеса в таком зацеплении принимают:

x₂ = - x₁,

а коэффициенты y = 0 и Δy = 0.

Диаметры вершин:

d_a = m (z + 2 + 2x).                                          (10.29)

         Диаметры впадин определяют по формуле (10.10), делительное межосевое расстояние – по формуле (10.13), межосевое расстояние a_w = a, угол зацепления α_w = α = 20º, коэффициент перекрытия ε_α определяют по формуле (10.19), передаточное отношение i₁₂ = - z₂/z₁.

Рис. 10.12. Геометрия зубчатого колеса

Г) Геометрия положительного зацепления.

В положительном зацеплении устраняется подрезание зубьев шестерни и улучшаются многие качественные показатели, и может быть обеспечено вписывание в стандартное межосевое расстояние. Делительное межосевое расстояние а – формула (10.10) - меньше заданного стандартного межосевого расстояния a_w, которое можно обеспечить при коэффициенте воспринимаемого смещения, определяемом по формуле (10.14). При этом угол зацепления определяют из формулы (10.12):