![]() ЗАДАНИЕ N 1 сообщить
об ошибке
Тема: Прямоугольный чертеж точки на две и три плоскости проекций
ЗАДАНИЕ N 1 сообщить
об ошибке
Тема: Прямоугольный чертеж точки на две и три плоскости проекций
Начало формы
Конец формы
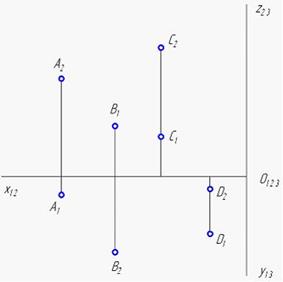
Проанализируйте
ортогональный чертеж точек А, В, С, D. В четвертой четверти пространства
расположена точка …
|
|
D |
||
|
В |
|||
|
A |
|||
|
С |
Решение: Плоскости проекций П1 и П2 делят пространство на четыре двугранных угла – четверти пространства. Положение проекций точек на эпюре Монжа (ортогональном чертеже) зависит от того, в какой четверти находится данная точка. Так, если точка расположена в четвертой четверти, то после совмещения плоскостей обе проекции окажутся лежащими под осью x12, так как точка имеет отрицательную аппликату (координату вдоль оси Oz) и положительную ординату (координату вдоль оси Oy). В данном случае такой точкой будет D.
![]() ЗАДАНИЕ N 2 сообщить
об ошибке
Тема: Метод проекций, виды проецирования
ЗАДАНИЕ N 2 сообщить
об ошибке
Тема: Метод проекций, виды проецирования
Начало формы
Конец формы
Свойство – «Если линии пересекаются, то их изображения пересекаются в проекции точки пересечения оригиналов» – является инвариантным (неизменным) ___ проецирования.
|
|
для любого вида |
||
|
только для центрального |
|||
|
только для параллельного |
|||
|
только для ортогонального |
Решение: Свойства оригинала, сохраняющиеся на изображении, называют инвариантными. При центральном проецировании инвариантными являются следующие свойства: 1) проекцией точки является точка; 2) проекцией кривой линии в общем случае является кривая линия; 3) сохраняется свойство инцидентности (взаимной принадлежности) точки и линии; 4) если линии пересекаются, то их изображения пересекаются в проекции точки пересечения оригиналов; 5) изображение проецирующей прямой вырождается в точку. Параллельные (следовательно, и ортогональные) проекции обладают всеми свойствами центральных проекций.
![]() ЗАДАНИЕ N 3 сообщить
об ошибке
Тема: Чертеж прямой линии, чертеж плоскости
ЗАДАНИЕ N 3 сообщить
об ошибке
Тема: Чертеж прямой линии, чертеж плоскости
Начало формы
Конец формы
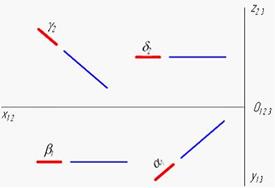
Проанализируйте
изображения плоскостей частного положения a,
b, g, d. Фронтально-проецирующей является плоскость …
|
|
g |
||
|
a |
|||
|
b |
|||
|
d |
Решение: Фронтально-проецирующая плоскость перпендикулярна фронтальной плоскости проекций и проецируется на нее в отрезок прямой линии, как в случае с плоскостью g.
![]() ЗАДАНИЕ N 4 сообщить
об ошибке
Тема: Чертеж многогранника. Чертеж поверхности вращения
ЗАДАНИЕ N 4 сообщить
об ошибке
Тема: Чертеж многогранника. Чертеж поверхности вращения
Начало формы
Конец формы
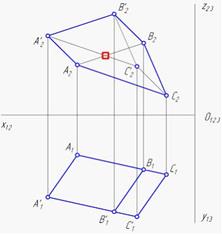
На фронтальной
проекции наклонной призмы ABCA’B’C’ видимость пока
не определена. Проанализируйте чертеж и продолжите утверждение: невидимым на
фронтальной проекции является ребро …
|
|
АВ |
||
|
A’C’ |
|||
|
B’C’ |
|||
|
СC’ |
Решение: На рисунке показан двухкартинный комплексный чертеж наклонной призмы. Видимость ребер на фронтальной проекции можно определить методом конкурирующих точек. Из анализа горизонтальной проекции следует, что точка на ребре A’C’ ближе к наблюдателю, чем точка на ребре АВ. Следовательно, ребро АВ на фронтальной проекции является невидимым. Точка С’ ближе всех точек призмы расположена к наблюдателю, поэтому все ребра, выходящие из этой точки, являются на фронтальной проекции видимыми.
![]() ЗАДАНИЕ N 5 сообщить
об ошибке
Тема: Способ прямоугольного треугольника
ЗАДАНИЕ N 5 сообщить
об ошибке
Тема: Способ прямоугольного треугольника
Начало формы
Конец формы
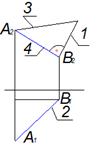
Натуральная
величина отреза прямой АВ – это длина отрезка, обозначенного на
чертеже цифрой …
|
|
3 |
||
|
2 |
|||
|
1 |
|||
|
4 |
Решение: Натуральная величина отрезка прямой, определенная способом прямоугольного треугольника (обозначена на чертеже цифрой 3), равна гипотенузе прямоугольного треугольника, один из катетов которого равен проекции отрезка (обозначен цифрой 4), а второй есть разность расстояний концов этого отрезка до той же плоскости проекций (обозначена на чертеже цифрой 1).
![]() ЗАДАНИЕ N 6 сообщить
об ошибке
Тема: Перпендикулярность на чертеже
ЗАДАНИЕ N 6 сообщить
об ошибке
Тема: Перпендикулярность на чертеже
Начало формы
Конец формы
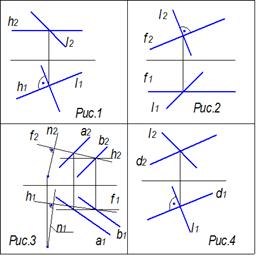
Прямая,
перпендикулярная плоскости общего положения, показана на рисунке …
|
|
3 |
||
|
4 |
|||
|
1 |
|||
|
2 |
Решение: Прямая перпендикулярна плоскости на чертеже, если ее горизонтальная проекция (n1) перпендикулярна горизонтальной проекции горизонтали этой плоскости (h1), а фронтальная проекция прямой (n2) перпендикулярна фронтальной проекции фронтали этой плоскости
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.