Выбор двигателя-прототипа с определением массогабаритных показателей и степени не уравновешености, страница 2

M_e=316·3·10⁴/(π·100)= 30267.52  Н×м

Удельный эффективный расход топлива

                                        

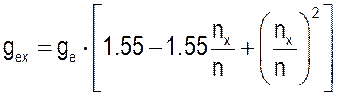
g_e=158·(1,55-1,55·(100/500)+(100/500)²)=202.24г/кВт×ч

Часовой расход топлива

                                                         

G_T=10^-3·202,24·316.8=64.07

кг/ч.

Расчеты для определенных выше режимов частоты вращения коленчатого вала производим  в табл. 2.

Таблица 2

Расчетные данные для построения внешней скоростной характеристики

n	Ne	Me	ge	Gt
об/мин	кВт	Н·м	г/кВт×ч	кг/ч
100	316,80	30267,52	202,24	64,07
150	503,55	32073,25	185,65	93,48
200	697,20	33305,73	172,22	120,07
250	888,75	33964,97	161,95	143,93
300	1069,20	34050,96	154,84	165,55
350	1229,55	33563,69	150,89	185,53
400	1360,80	32503,18	150,10	204,26
450	1453,95	30869,43	152,47	221,68
500	1500,00	28662,42	158,00	237,00

2.2.  Построение внешней скоростной характеристики

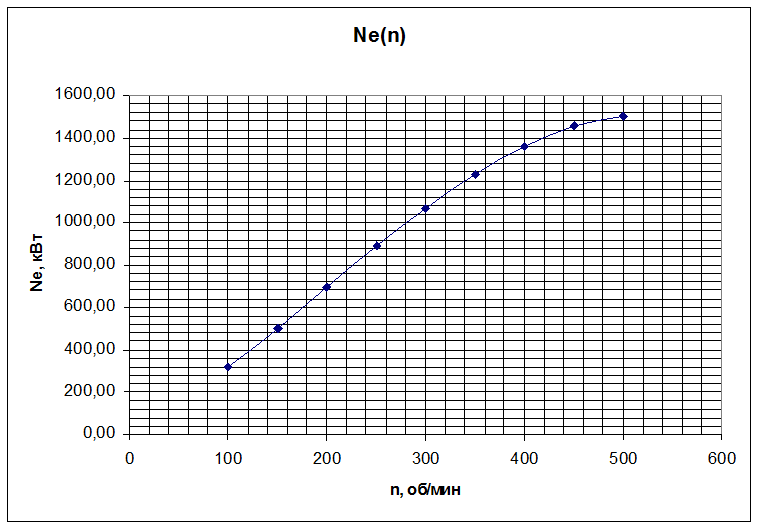
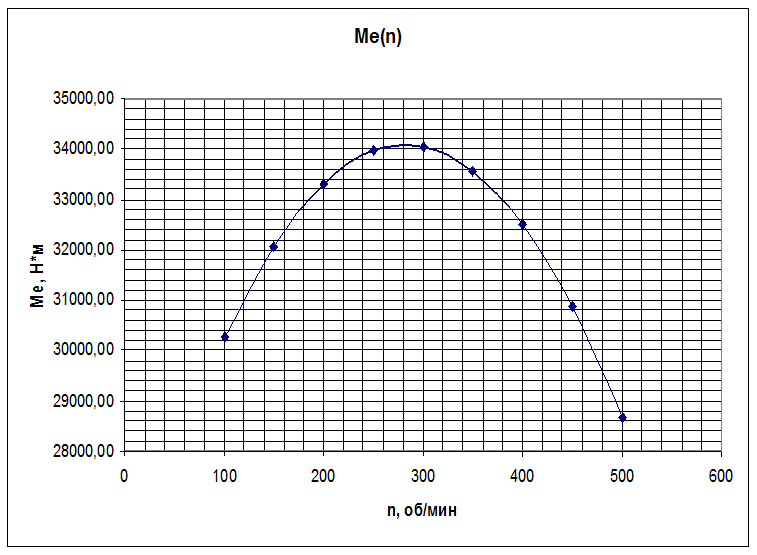
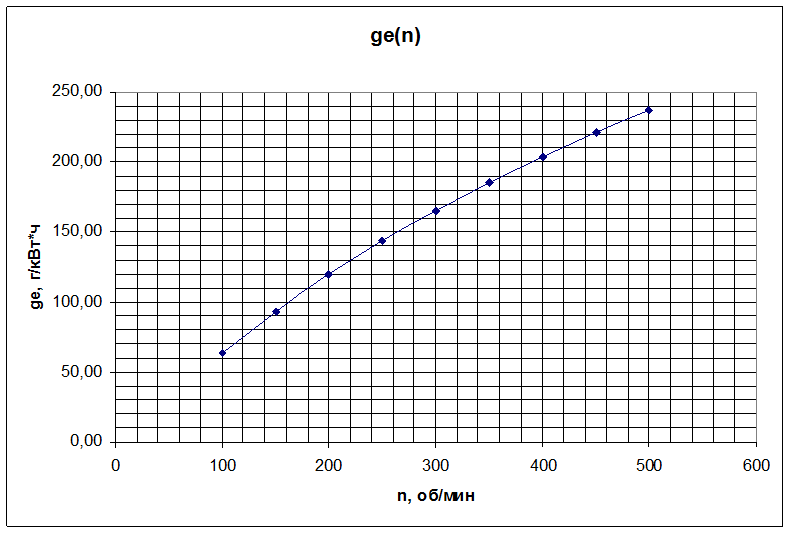
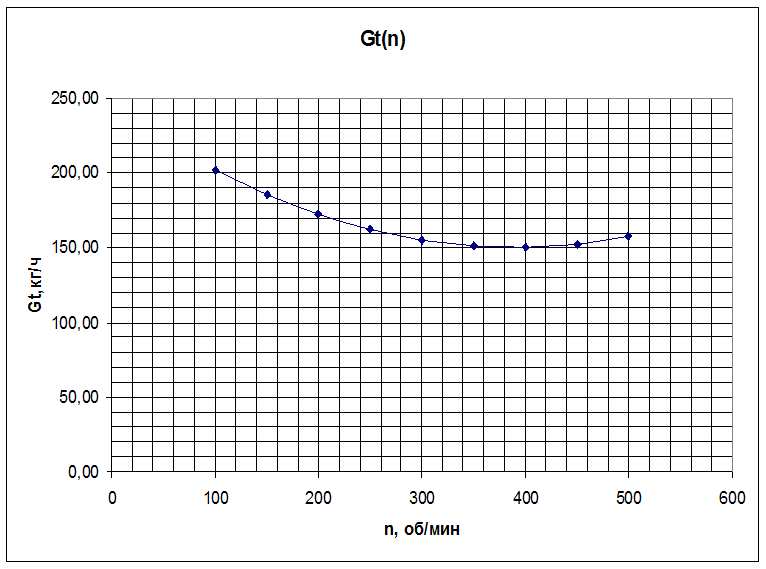
По данным табл. 2 строим внешнюю скоростную характеристику двигателя, представленную на рис. 1.

Рис. 1. Внешняя скоростная характеристика двигателя

 

 

3.  Тепловой баланс двигателя

η_e=0,46 – эффективный КПД;

η_cool=0,21 – часть тепла, отводящаяся от дв. с охлаждающей жидкостью;

η_н=0,33 – часть тепла, отводящаяся с отработавшими газами;

Коэфицент используемого тепла равен:

КИТ= η_e+a·η_cool+b·η_н=0,7

Поберем коэфиценты а и b

a	b	a*Qн	b*Qcool
0,7	0	807,00	0,00
0,6	0,1	657,60	71,70
0,5	0,2	538,00	143,00
0,4	0,3	430,40	215,10
0,3	0,4	322,80	286,80

a·Q_H=((N_e η_н)/ η_e)·0,5=((1500·0,33)/0,46)·0,5=538 кВт

b·Q_cool=((N_e η_cool)/ η_e)·0,2=((1500·0,21)/0,46)·0,=143 кВт

4.  Расчет подвески двигателя

4.1.  Внешние неуравновешенные силы инерции и моменты сил

Работа кривошипно-шатунных механизмов поршневых ДВС связана с возникновением сил инерции. Наибольшее действие на фундаменты двигателей оказывают силы первого и второго порядков возвратно-движущихся масс и центробежные силы вращающихся неуравновешенных масс, а также моменты этих сил.

Определим силы инерции первого и второго порядков и центробежные силы работе цилиндров  по формуле1-3-7-5-8-6-2-4-1 :

1 8                                  P_R1P_R2

 

      4 5                                   3 6        P_R4P_R5                                                  P_R3P_R6

 

2 7                                                   P_R2P_R7

C_I1C_I2                           C_II1C_II2 C_II7C_II8

C_I4C_I5                                       C_I3C_I6                                                          

C_I2 C_I7                                           C_II3C_II4 C_II5C_II6

∑P_R=0;

∑С_II=0;

∑C_I=0.

Определим амплитуды моментов сил:

∑М_R=0;

∑М_CI= 0;

∑М_CII=0,

Следовательно, можем полагать что дв. самоуравновешан по силам и моментам сил до II порядка включительно.

4.2.  Подбор упругих подвесок.

Резонансная частота наступит при n=100 об/мин, следовательно

ω_рез=πn/30=3,14·100/30=10,5 с^-1;

Частота упругих элементов k_уэ должна равняться ω_рез. Поэтому k_уэ=10,5 с^-1.

В свою очередь:

k_уэ²=с/m;

где с – жесткость упругого элемента, а m – масса установки равная 19·10³ кг. Отсюда:

c_об= k_уэ²·m=10,5·19·10³=2·10⁵ Н/м

Так как установка будет утановленна на четыре пружины, которые состовляют параллельную схему соединения, следовательно принимаем что жесткость каждой пружины считается следующим способом:

c_об=c₁+c₂+c₃+c₄;

поскольку пологаем что пружины одинаковы, то:

с_об=4с₁; 

с₁=0,5·10⁵ Н/м.

Теперь зная жесткость пружины, определим ее размеры.

с=G·r⁴/4R³n;

При радиусе провлки r=0,04 м;

R³·n=G·r⁴/4c=10¹¹·0,03⁴/4·0,5·10⁵=0,405

 

Примем количество витков n=4:

R³=0,405/4=0,101

R=0,46 м

Статический прогиб пружины равен: