Транспортная задача (четыре карьера, производящих строительные материалы)

Министерство образования Российской Федерации

Санкт-Петербургский  государственный горный               университет      

Транспортная задача

По дисциплине:  Экономико-математические методы и моделирование

(наименование учебной дисциплины согласно учебному плану)

Выполнил: студент  гр. ГК-08-1412            ______________                          / Семенов С.О. /

^{(подпись)                                                   (Ф.И.О.)}

Проверил: доцент                                 ______________                                /_____________/

                                                                                                                                 ^{(подпись)                                                                                 (Ф.И.О.)}

Санкт-Петербург

2012 год

Транспортная задача

Задание:

Имеется четыре карьера, производящих строительные материалы, и четыре потребителя сырья строительных материалов. Известны объемы производства на каждом карьере, потребности в их продукции каждого из потребителей, а также стоимость перевозки 1 т продукции с I-го карьера к J-му потребителю. Определить, при каких объемах грузоперевозок от I-го поставщика к J-му потребителю суммарная стоимость перевозок будет минимальной.

1.  Решить задачу средствами Excel (Надстройка «Поиск решения)

2.  Решить задачу аналитически

; 

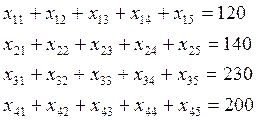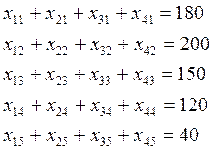
F=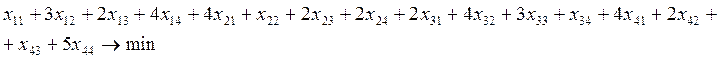

Построим  математическую модель данной задачи.

Вычислим суммарные запасы: 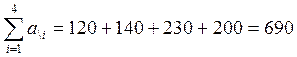      и суммарные потребности: .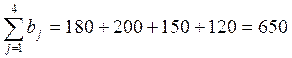  

Так как суммарные запасы не равны суммарным потребностям, то данная задача является задачей открытого типа. Сведем ее к задаче закрытого типа – добавим фиктивного потребителя.

Целевая функция:

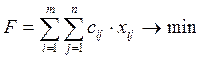, где

F - суммарная стоимость всех перевозок;

c_ij - стоимость перевозки единицы груза от i-го поставщика j-му потребителю;

x_ij - объем грузоперевозок от i -го поставщика j -му потребителю.

Требование о вывозе груза у всех поставщиков порождает следующие фазовые ограничения:

,                          

а требование об удовлетворении потребностей в  грузе всех потребителей порождает такие фазовые ограничения:

 .                         

Соотношения

                        

являются естественными ограничениями.

Построим опорное решение методом «северо-западного» угла.

В результате этой процедуры m+ n -1  клеток будут иметь перевозки, остальные –   будут пустыми. Достоинством метода «северо-западного» угла является его простота, недостатком – его «удаленность» от оптимального решения (т.е. при построении оптимального решения требуется большее количество шагов – итераций), поскольку при его построении не учитываются цены перевозок.

В результате имеем таблицу с 8 заполненными клетками, что соответствует теории:  m+n-1 =4+5-1=8

Суммарная стоимость перевозок равна

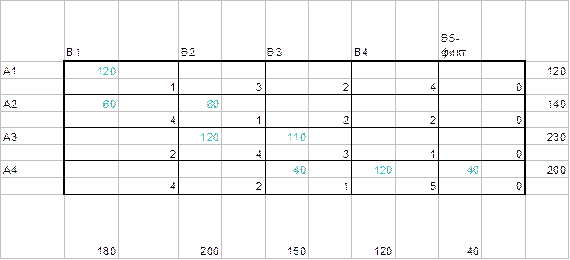
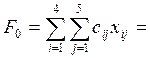120*1+60*4+80*1+120*4+110*3+40*1+120*5+40*0=1890

Рассчитаем систему потенциалов для этого решения.

Введем дополнительный столбец и дополнительную строку (и ) и занесем вычисленные значения потенциалов в полученные клетки.

Вычислим значения невязок для всех клеток без перевозок по формуле  и отметим невязки, которые не удовлетворяют (невязки больше нуля). Выберем клетку с большим нарушением и построим замкнутый цикл с началом в этой клетке. В качестве остальных вершин выберем клетки с перевозками. Нечетные вершины образуют положительную полуцепь, четные – отрицательную. Величина, определяющая перераспределение, равна наименьшему значению из перевозок, стоящих в четных вершинах цикла. Вычислим новые значения для узлов контура. В четных вершинах значения уменьшаются, в нечетных – увеличиваются .

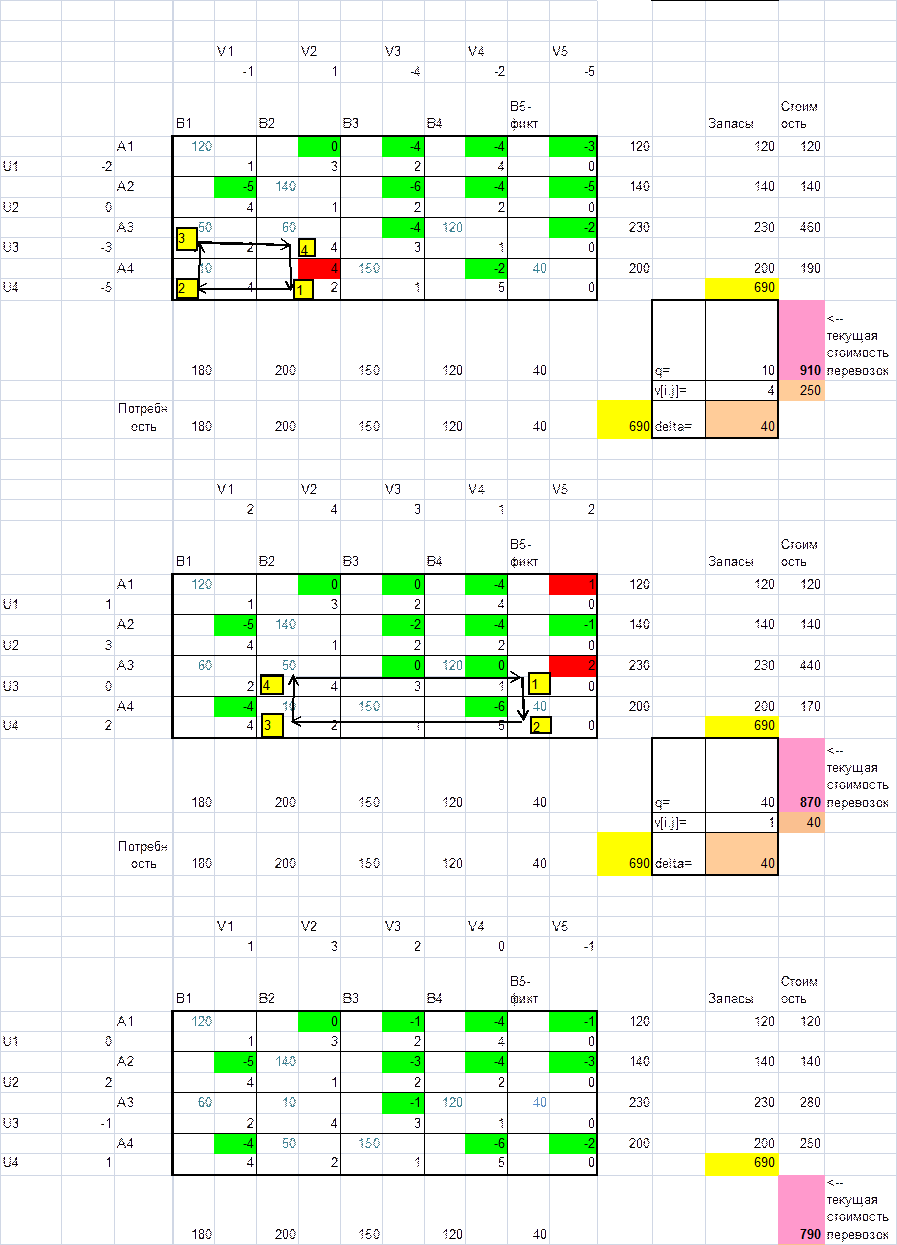
Мы получили решение без положительных невязок. Отсюда можно сделать вывод о том, что суммарная стоимость перевозок будет минимальной и равной  790

Решение транспортной задачи в Excel

Решим данную задачу в Excel, используя надстройку «Поиск решения».

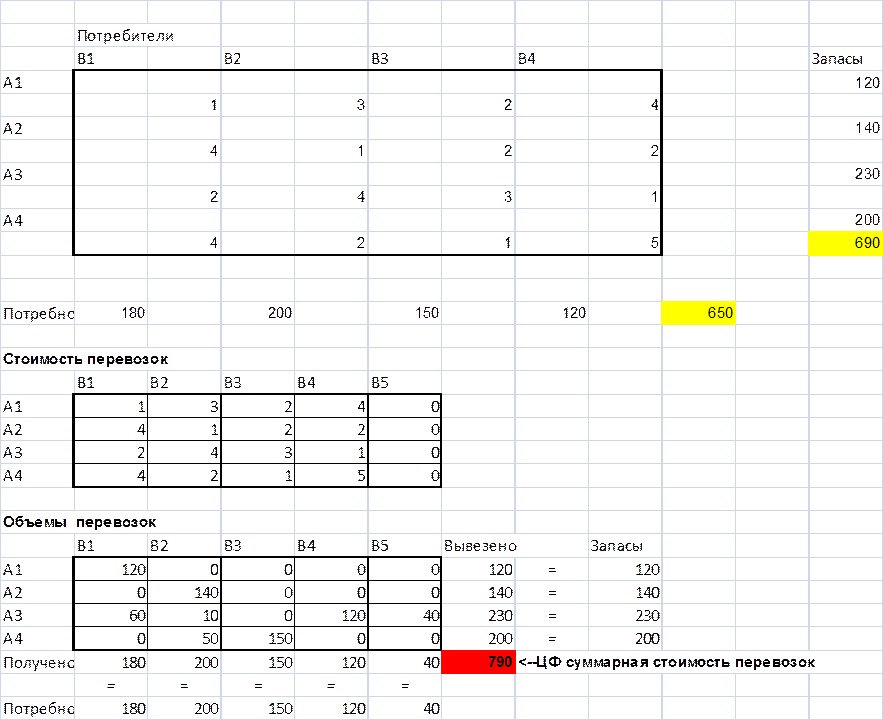
Заметим, что результаты полностью совпадают с результатами, полученными ранее методом потенциалов.