Приведенные выше методы, кроме метода створов, являются довольно трудоемкими как с точки зрения осуществления их на оползневом склоне, так и камеральной обработки результатов. Кроме того, эти методы не обеспечивают определения равноточного положения оползневых точек по площади склона. Этот недостаток можно в некоторой степени компенсировать соответствующей математической обработки результатов. Метод фотограмметрии обладает достаточно высокой точностью и большой информативностью, однако в условиях заселенных и застроенных склонов его применение ограничено.
Определение деформации по фотоснимкам
Предотвращение оползней и обрушении откосов на карьерах, обеспечение нормальной работы инженерных сооружений и горных механизмов - важное условие безаварийной и четкой работы горного предприятия. Решить эти задачи можно путем постановки систематических наблюдений с привлечением самых современных методов. Если доступ на объекты для выполнения непосредственных измере6ний невозможен, то только по фотоснимкам можно получить информацию о его состоянии. Рассмотрим, как это можно осуществить.
Деформация в
данной точке характеризуется вектором смещения ![]() составляющие
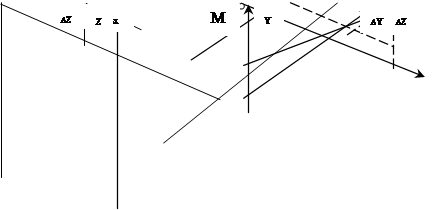
которого DХ, DY, DZ определяются в пространственной фотограмметрической системе
координат (рис.1) либо в системе геодезических координат. Модуль вектора
смещения и его направление находят путем фотографирования объекта с одной или
двух точек пространства и последующей камеральной обработкой материалов съемки.
Фотографирование осуществляют дважды при постоянных элементах ориентирования
снимков. Если в промежутке времени между фотографированием точка М1
(вектор смещения
составляющие
которого DХ, DY, DZ определяются в пространственной фотограмметрической системе
координат (рис.1) либо в системе геодезических координат. Модуль вектора
смещения и его направление находят путем фотографирования объекта с одной или
двух точек пространства и последующей камеральной обработкой материалов съемки.
Фотографирование осуществляют дважды при постоянных элементах ориентирования
снимков. Если в промежутке времени между фотографированием точка М1
(вектор смещения ![]() не равен нулю), то вектор на
снимке
не равен нулю), то вектор на
снимке ![]() также не равен нулю при условии, что точи
М1 и М2 не лежат на одном проектирующем луче.
также не равен нулю при условии, что точи
М1 и М2 не лежат на одном проектирующем луче.
 |
 |
|
Составляющие Dx,
Dz вектора ![]() , называемые смещениями по осям координат,
определяют в плоской системе координат оxz снимка, которая вводится с помощью изображений
координатных меток.
, называемые смещениями по осям координат,
определяют в плоской системе координат оxz снимка, которая вводится с помощью изображений
координатных меток.
коллинеарны, поэтому пропорциональны проекции этих векторов на оси X, Y, Z, т.е.
|
|
(1) |
Где x2, z2 -
координаты точки m2 в системе координат
снимка; X1, Y1, Z1 –
пространственные координаты точки М1; DХ,
DY, DZ – составляющие
вектора ![]() на оси фотограмметрической системе
координат.
на оси фотограмметрической системе
координат.
Из пропорции (1) имеем
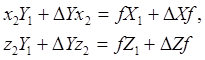
или с учетом того, что
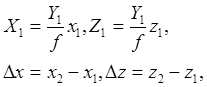
получим
|
|
(2) |
С помощью системы уравнений (2) нельзя вычислить составляющие вектора смещения точки объекта, даже если отстояние Y1 известно, так как в двух уравнениях имеем три неизвестных - DХ, DY и DZ. Однако способ, основанный на изучении деформации объектов по фотоснимкам, полученным с одной точки пространства, встречается на практике. Его называют фотограмметрическим и применяют в том случае, если направление вектора смещения точки пространства параллельно плоскости снимка, т.е еще до постановки наблюдений за объектом известно, как установить камеру, чтобы составляющая DY равнялась нулю.
В фотограмметрическом способе составляющие DY и DZ вычисляют по формулам
|
|
(3) |
которые получают путем подстановки DY=0 в уравнения (2).Отстояние Y определяют, как правило, один раз любым известным в геодезии или фотограмметрии способом.
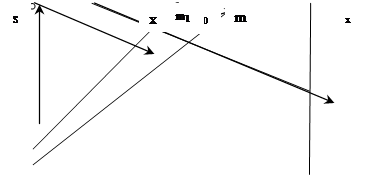
В этом случае, когда фотограмметрический способ наблюдения за деформированием объекта использовать нельзя, фотографирование производят с двух точек пространства (рис.2), направляя главные лучи под углом g друг к другу (конвергентный способ). Частным случаем конвергентного способа является стереофотограмметрический, когда угол конвергенции g=0.
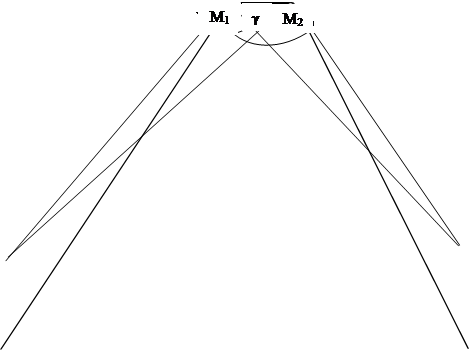 |
 |
|
В конвергентном способе можно составить четыре уравнения вида (2): два для левого и два для правого снимка. Одно из уравнений будет избыточным, так как составляющие вектора смещения, полученные в фотограмметрической системе координат левого и правого снимков, связаны очевидным соотношением
|
|
(4) |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.