Предельный угол полного внутреннего отражения, страница 2

Дать определение тонкой линзы, построить изображение, создаваемое тонкой положительной линзой. Вычислить оптическую силу линзы, заднее фокусное расстояние которой (в метрах) равно отношению 1/k, где k – сумма двух последних цифр в шифре зачетной книжки студента.

Решение:

1.  Линза (нем. lines от лат. lens – чечевица) –это оптическая деталь, ограниченная двумя преломляющими поверхностями, имеющими сферическую (от греч. sphaira – шар) (или асферическую) форму, причем одна из поверхностей может быть плоской. Оптическая ось линзы проходит через центры кривизны ее сферических поверхностей и является осью симметрии линзы. Линза представляет собой простейшую оптическую систему, обычно имеет круглую форму, но встречаются линзы прямоугольные, квадратные и др.

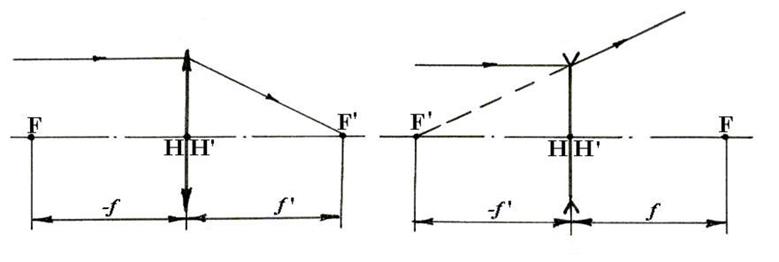
Обычно в линзах расстояние между главными плоскостями мало и можно считать, что они совпадают. Тогда линзу можно рассматривать как идеальную оптическую систему и заменить ее главными плоскостями, считая толщину d равной нулю (рис. 2 а), б))

а)                                                              б)

Рис. 2. Тонкие линзы.

Тонкая (бесконечно тонкая) линза – линза, в которой расстояние ∆_НН  между главными плоскостями и толщина d равны нулю (∆_НН =0, d=0). Другими словами, тонкой называется линза, толщина которой значительно меньше радиусов ограничивающих ее сферических поверхностей.

В тонких линзах преломление луча происходит на совмещенных главных плоскостях, которые на чертеже показываются отрезком прямой, перпендикулярной оптической оси, со стрелками на концах (рис. 2. а, б,). Для положительных линз () острия стрелок направлены вверх и вниз от оси (рис 2. а), а для отрицательных линз () – по направлению к оптической оси (рис. 2. б). 

Оптическая сила линзы (величина, обратная фокусному расстоянию F) вычисляется по формуле:

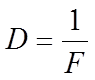
2. Построим изображение предмета AB=y при различных его положениях относительно тонкой линзы в воздухе. Положение предмета и его изображения до и после линзы обозначим через и соответственно.

Линза положительная (f ′ > 0), n = n′ = 1 (рис. 3 а, б, в, г, д)

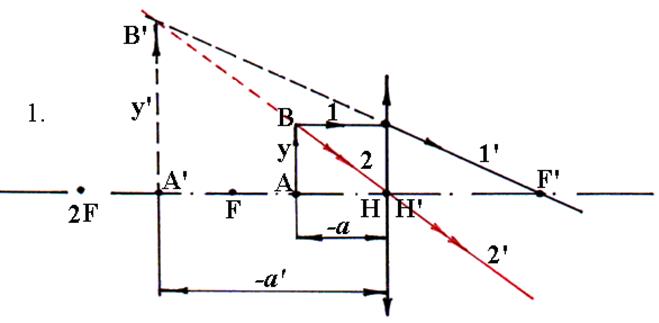
1) Предмет АВ расположен перед передним фокусом линзы (а < f). Изображение – прямое, увеличенное, мнимое, т.к. получается на пересечении продолжений лучей 1′ и 2′, вышедших из линзы.

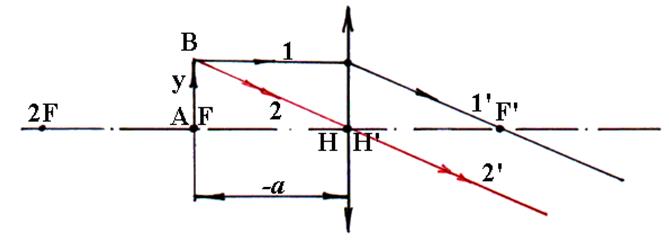
2) Предмет АВ расположен в переднем фокусе линзы (т.F) (а = f). Лучи 1′ и 2′ выходят из линзы параллельными и изображение предмета получается в бесконечности.

3) Предмет АВ расположен между точкой F и точкой 2F (f < a < 2f). Изображение –перевернутое, увеличенное, действительное.

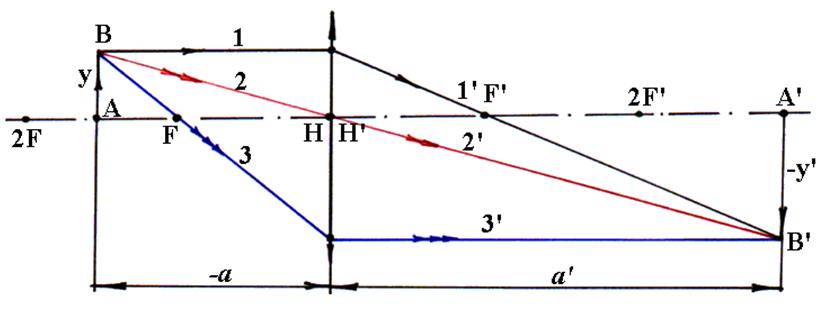
4) Предмет расположен в точке 2F (в двойном переднем фокусе) (а = 2f). Изображение перевернутое, по величине равное предмету, действительное.

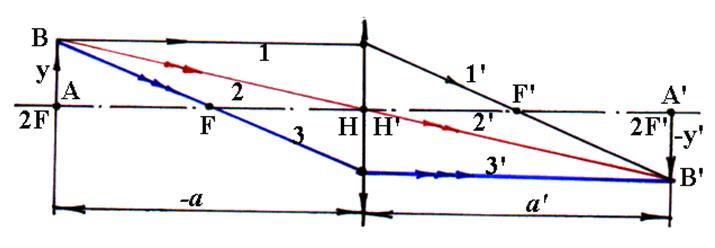
Рис.3. Построение изображения предмета АВ при различных положениях относительно фокусов в тонкой положительной линзе

3.  Вычислим оптическую силу линзы, заднее фокусное расстояние которой (в метрах) равно отношению 1/k, где k – сумма двух последних цифр в шифре зачетной книжки, т.е. k = 0+1=1.

Исходные данные		Оптическая сила линзы
		Формула вычисления	Значение
	1 м		1 дптр

Оптическая сила линзы равна D=8 дптр.

Задание 4.

Построить изображение, создаваемое с помощью лупы, вычислить увеличение рассматриваемого предмета, если фокусное расстояние лупы (в миллиметрах) равно сумме количества букв в фамилии студента и последней цифры его шифра. Затем вычислить общее увеличение микроскопа, если увеличение его объектива равно сумме цифр в шифре зачетной книжки студента, а увеличение окуляра – количеству букв в его фамилии.

Решение:

1. Изображение, создаваемое с помощью лупы. Лупа может давать мнимое увеличенное изображение на конечном расстоянии или бесконечно удаленное увеличенное изображение. Поэтому возможны два основных случая расположения предмета -  a < f или a = f .

В первом случае наблюдаемый предмет у (рис. 4) помещают перед лупой на расстоянии a < f ,между передним фокусом (т. F) и передней главной точкой (т.H). Для построения изображения точки А этого предмета используем два луча, исходящих на нее: один, параллельный главной оптической оси, после преломления проходит через фокус; другой, проходящий через главный оптический центр линзы, не изменит своего направления. Изображение А’ точки А получится в точке пересечения продолжений преломленных лучей. Аналогично получаем изображение B’  точки B. Следовательно, изображение A’B’ предмета АB будет мнимое, увеличенное и прямое.