sentence(S,S0):-agent(S,S1), effect(S1,S2), object(S2,S3),instrument(S3,S4),
position(S4,S5),time(S5,S0).
sentence(S,S0):-agent(S,S1), effect(S1,S2), object(S2,S3),instrument(S3,S4),
position(S4,S5),time(S5,S6),purpose(S6,S0).
agent([X|S0],S0):-pronoun(X).
agent(S,S0):-noun_group(S,S0).
agent([X|S0],S0):-name(X). и т.д.
Вопросы естественно-языковых интерфейсов систематически рассмотрены в [10]. За основу данной для данной лабораторной работы взят материал из [6], гл.9.
Лабораторная работа №6
Тема: Автоматическое доказательство теорем
Цель работы: Изучение машинных методов доказательства теорем для простых формальных систем
Задание
§ Рассмотреть заданную формальную систему и сформулированную в рамках данной системы теорему. Доказать эту теорему “в ручную”.
§ Написать программу автоматического доказательства теорем на Прологе, используя основные свойства среды Пролога – поиск с возвратом и унификацию.
§ Использовать метод Сиклосси-Маринова (реализовать соответствующую эвристику) для ограничения пространства поиска доказательства.
§ Ввести в программу возможность вывода хода доказательства.
Методические указания
Определение формальной системы в контексте искусственного интеллекта приводится в [3, гл.3], [7]. В [3] приводятся основные подходы к проблеме автоматического доказательства теорем. В частности рассматривается простейший подход, основанный на методе направленного перебора.
Рассмотрим пример формальной системы для исчисления высказываний. Рассматриваются следующие шесть правил вывода:
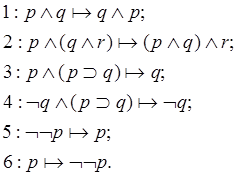 (1)
(1)
Пусть
требуется доказать теорему:![]() (2)
(2)
Для построения программы автоматического доказательства используем язык Пролог, поскольку на нем естественным образом можно записать правила вывода, реализовать механизм поиска и унификации. Любопытные могут, например, попробовать написать эту программу на Паскале и убедится, на сколько это сложнее.
Для начала необходимо выбрать способ представления логических выражений:
DOMAINS EXPR=con(EXPR,EXPR); % конъюнкция
impl(EXPR,EXPR); % импликация
no(EXPR); % отрицание
var(symbol). % переменная
Основной предикат, который реализует вывод определен ниже. Первым аргументом предиката является входное выражение, в нашем случае – условие теоремы. Второй аргумент – преобразованное согласно правилам вывода выражение. Поскольку этот предикат недетерменированный, то его необходимо определить таким образом, чтобы он смог сгенерировать все возможные следствия из условия теоремы. Если среди этих следствий окажется заключение теоремы, то она будет считаться доказанной.
PREDICATES
nondeterm reduce(EXPR,EXPR)
CLAUSES
reduce(var(X),var(X)). reduce(con(P,Q),X):- reduce(P,P1),reduce(Q,Q1),reduce(con(Q1,P1),X). %1 reduce(con(P,con(Q,R)),con(con(P1,Q1),R1)):- %2
reduce(P,P1),reduce(Q,Q1),reduce(R,R1).
reduce(con(P,impl(P,Q)),Q1):- %3
reduce(Q,Q1).
reduce(con(no(Q),impl(P,Q)),no(P1)):- %4
reduce(P,P1).
reduce(con(no(no(Q)),impl(P,no(no(no(Q))))),no(P1)):- %4.1
reduce(P,P1).
reduce(no(no(P)),P1):reduce(P,P1). %5
reduce(X,no(no(X))). %6
GOAL
reduce(con(var(t), impl(var(s), no(var(t)))),X),
write(X),nl,X=no(var(s)).
Приведенные выше правила преобразования, отражающие соответственно правила вывода из нашей формальной системы, определены рекурсивно. Поэтому важным является порядок их применения. Для корректной работы программы необходимо иметь в виду следующие моменты:
- некоторые правила вывода являются экстенсивными (см. правила 1,6). Это значит, что к результату правила вывода применимо тоже правило. Следовательно может возникнуть ситуация, когда будет генерироваться либо повторяющаяся через шаг последовательность(правило 1), либо “разбухающее” выражение (правило 6);
- поочередное применение правил 5,6 возвращает ситуацию в прежнюю позицию.
Поэтому приведенный текст программы должен быть откорректирован таким образом, чтобы исключить указанные моменты. В [3] рассмотрена простая эвристика, предложенная Сиклосси и Мариновым. Ее смысл состоит в том, чтобы экстенсивные правила применять только в случае последней необходимости и один раз.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.