Экономическая игра «Дельта». Оценка производственной функции, страница 2

Взяв логарифм, получим следующую таблицу

Периоды

П1

П2

П3

С1 (млн.)

С2 (млн.)

С1 (млн.)

С2 (млн.)

С1 (млн.)

С2 (млн.)

0

2,302585093

4,248495242

2,197224577

2,708050201

2,197224577

1,098612289

1

2,302585093

4,248495242

2,351375257

2,862200881

2,128231706

1,098612289

2

2,302585093

4,248495242

2,457535453

2,968361077

2,062803901

1,033184483

3

1,791759469

3,737669618

2,197224577

2,708050201

1,945910149

0,916290732

4

1,614027365

3,559937514

2,90690106

3,417726684

1,722766598

0,693147181

5

1,871802177

3,817712326

3,044522438

3,555348061

2,128231706

1,098612289

6

- INF

- INF

- INF

- INF

2,563948857

1,385293861

7

1,609437912

3,555348061

2,708050201

3,218875825

2,459588842

1,280933845

8

2,302585093

4,248495242

2,785011242

3,295836866

2,222459049

1,043804052

9

2,302585093

4,248495242

3,044522438

3,555348061

2,258424197

1,079769201

10

2,197224577

4,143134726

3,072693315

3,583518938

2,274185618

1,17557333

Проделаем вычисления в среде Mathcad:

                                

              

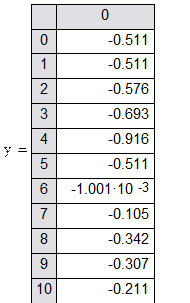
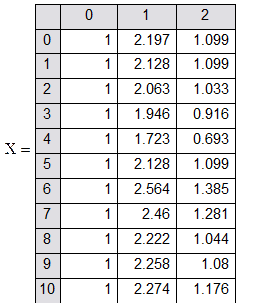
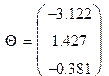
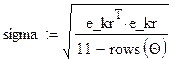
Продукт \ Параметр

П1

1

1

1,74E-09

2,206E-10

П2

0,333

1

-2,22E-07

2,278E-9

П3

0,044

1,427

-0,381

0,05

где параметр  находится по формуле .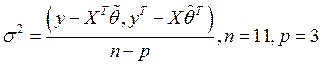

Теперь сравним значения найденной функции с истинными, подставив в функцию Коба-Дугласа соответствующие значения для каждого продукта.

Периоды

П1

П2

П3

КБ

ист

КБ

ист

КБ

ист

0

10,00000007

10

2,996998195

3

0,665845608

0,6

1

10,00000007

10

3,496497774

3,5

0,603414886

0,6

2

10,00000007

10

3,888105433

3,892

0,5635001

0,562

3

6,000000039

6

2,996998195

3

0,498646111

0,5

4

5,023000031

5,023

6,093895368

6,1

0,394843109

0,4

5

6,500000043

6,5

6,992994471

7

0,603414886

0,6

6

0

0

#ДЕЛ/0!

0

1,007419804

0,999

7

5,000000031

5

4,994996424

5

0,903238932

0,9

8

10,00000007

10

5,394596046

5,4

0,704824864

0,71

9

10,00000007

10

6,992994471

7

0,731845113

0,736

10

9,000000065

9

7,192794268

7,2

0,721663579

0,81

На графиках это выглядит следующим образом:

1. первый продукт.

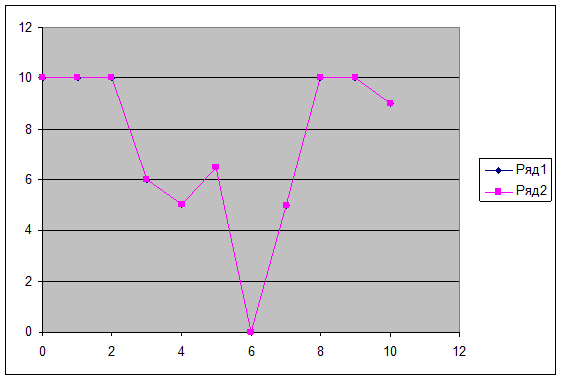
2. Второй продукт.

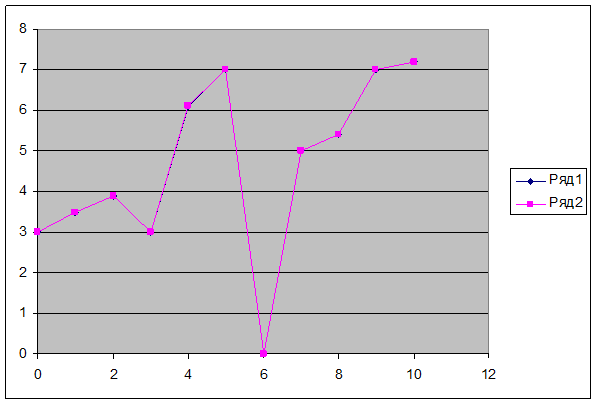
3. Третий продукт.


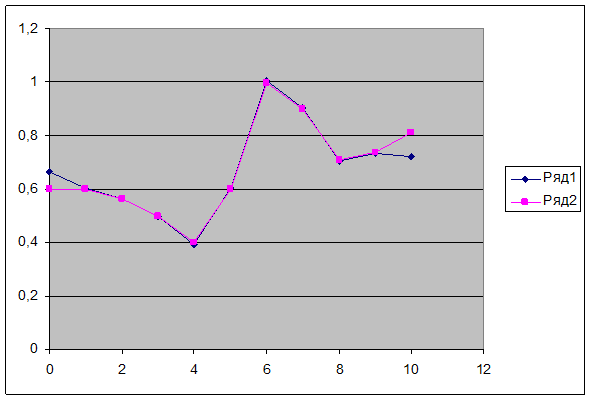
Выводы

Исходя из оценок коэффициентов функций Коба-Дугласа и параметру контроля , можно сказать, что ближе всего к истинному распределению  оценки параметров функции производства первого и второго продуктов, достаточно близка также оценка параметров функции производства третьего продукта.

Скачать файл