Экономическая игра «Дельта». Оценка производственной функции

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

Кафедра прикладной математики

Контрольная работа

Экономическая игра «Дельта»

Факультет:  ПМИ

Группа:  ПМ-13

Студенты:   Ерёмина М. Е.

Дуркин Д. С.

Преподаватель: Лисицин Д. В.

Новосибирск, 2005 г.

Условие задачи

Оценить производственную функцию деловой игры «Дельта» для каждого продукта, если известно, что функция производства – функция Коба-Дугласа и зависит только от количества сырья первого и второго типа. В качестве метода оценки воспользоваться методом наименьших квадратов.

Анализ решения задачи

Запишем функцию Коба-Дугласа:

.

Данная функция не является линейной функцией от параметров, которая имеет вид

,

Для приведения ее к линейному виду, прологарифмируем функцию Коба-Дугласа, и получим

, где параметры  требуют определения.

Сформулируем задачу как задачу для линейной функции по параметрам. Пусть  – матрица значений функций в точках исследования,  – вектор параметров, – вектор выходных переменных. Будем минимизировать функцию

, .

Минимизируем функцию по вектору параметров и получим

.

Тогда определим матрицу значений и вектора следующим образом:

, , .

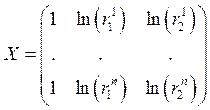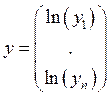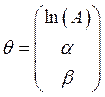Решение задачи

Известно следующее распределение количества ресурсов на производство одной единицы продукта:

Зная количество произведённого продукта в каждый период можно оценить количество затрачиваемых ресурсов.

Приведём таблицу производства продуктов по периодам:

Взяв логарифм, получим следующую таблицу

В результате получим следующие распределения сырья по продуктам во всех периодах: