Устойчивые методы оценивания параметров регрессии, страница 2

Квадрат разности между оценкой вектора неизвестных коэффициентов и истинным значением параметров минимален при .  Таким образов, ИМНК дает наилучшие результаты, когда 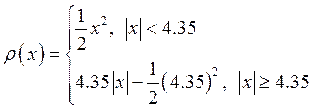, весовая функция имеет вид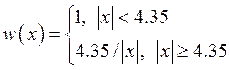

ИМНК

0,950015

1,512933

-2,56792

0,007278

МНК

-0,93018987    

0,3033535

-3,2385423

5,70304051

За счет наличия 4 достаточно существенных выбросов обычный метод МНК дает заметно низкие результаты, в то время как итерационный МНК дает вполне приемлемые результаты.

1

1

2

2,058792

2,004999

-0,005

0,053793

2

1

0,75

0,76177

0,721041

0,028959

0,040729

3

1

-0,5

-0,55396

-0,56292

0,062918

0,008958

4

1

-1,75

-1,87926

-1,84688

0,096876

-0,03239

5

1

-3

-3,05016

-3,13083

0,130835

0,080671

6

1

2,75

2,826312

2,761465

-0,01147

0,064847

7

1

1,5

1,508202

1,477507

0,022493

0,030695

8

1

0,25

0,222947

0,193549

0,056451

0,029399

9

1

-1

-0,99078

-1,09041

0,09041

0,099631

10

0,063308

-2,25

-8,98046

-2,37437

0,124368

-6,6061

11

1

3,5

3,512607

3,517932

-0,01793

-0,00533

12

1

2,25

2,291399

2,233974

0,016026

0,057426

13

1

1

1,056154

0,950015

0,049985

0,106139

14

0,017984

-0,25

-23,5889

-0,33394

0,083943

-23,255

15

1

-1,5

-1,52593

-1,6179

0,117901

0,091968

16

1

4,25

4,173192

4,274399

-0,0244

-0,10121

17

1

3

2,972698

2,99044

0,00956

-0,01774

18

0,472757

1,75

2,591118

1,706482

0,043518

0,884636

19

1

0,5

0,410544

0,422523

0,077477

-0,01198

20

1

-0,75

-0,83882

-0,86143

0,111435

0,022619

21

1

5

4,99475

5,030865

-0,03087

-0,03611

22

0,022169

3,75

-15,1182

3,746907

0,003093

-18,8651

23

1

2,5

2,555675

2,462948

0,037052

0,092727

24

1

1,25

1,248423

1,17899

0,07101

0,069433

25

1

0

0,08719

-0,10497

0,104968

0,192158

Выводы:

Был рассмотрен случай, когда в выборке подчиненной стандартному нормальному распределению присутствую выбросы, имеющие тот же закон распределения, но принудительно увеличенные в 300 раз. В виду того, что обычный МНК не учитывает это, полученная оценка вектора неизвестных коэффициентов не применима. В итерационном МНК присутствует весовая функция, которая сглаживает выбросы. Чем больше величина выброса, тем меньше значение весовой функции; результаты присутствую в последней таблице. В процедуре ИМНК присутствует параметр , который отвечает за остановку алгоритма. Уменьшение этого параметра значительно увеличивает количество вычислений, но при этом оценка приближается к точному значению.

Скачать файл