Министерство Образования Российской Федерации
Новосибирский Государственный Технический Университет
Кафедра программного обеспечения и баз данных
Лабораторная Работа №9
по курсу: “Планирование и анализ экспериментов”
Факультет: ПМИ
Группа: ПМ-11
Студенты: Шершнев Д.
Важенин И.
Преподаватели: Лисицин Д.В.
Вариант: 1
Новосибирск 2005
Тема работы.
Устойчивые методы оценивания параметров регрессии.
Порядок выполнения.
1. Изучить методы устойчивого оценивания параметров регрессии и метод поиска значений оценок.
2. Выбрать линейную регрессионную модель. По данной модели сгенерировать экспериментальные данные, содержащие выбросы. Выбросы можно смоделировать, увеличив в несколько десятков раз величину ошибки в нескольких точках выборки. Проконтролировать наличие выбросов в выборке визуально.
3. Разработать программу, реализующую поиск оценок параметров итерационным МНК для функции потерь, указанной в варианте.
4. Выбрать
несколько значений параметра функции потерь (включая указанные в варианте) и
найти значения М-оценок для каждого из них. Вычислить МНК-оценку. Сравнить
качество всех полученных оценок по величине 
,
выбрать наилучшее значение параметра функции потерь.
5. Оформить отчет, включающий в себя
– постановку задачи;
– полученный набор данных и значения ошибок наблюдений;
– оценки параметров и результаты их сравнения;
–
для наилучшей из оценок: значение весов наблюдений на последней итерации
и значения 
;
– текст программы.
Задание.
Функция Хьюбера:
.
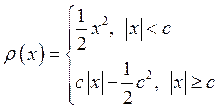
Рекомендуемые значения параметра – 1.5, 3.0.
Выберем
следующую линейную регрессионную модель: 
.
Пусть
. Равномерно разместим внутри квадрата 
16 точек.
Пусть вектор истинных значений 
. Для генерации ошибки
воспользуемся генератором случайно нормально распределенных величин с
параметрами 
. Для
получения выбросов увеличиваем значение ошибки 
в 300
раз. Тогда получим следующие данные:
|
N |
|
|
|
|
|
1 |
-1 |
-1 |
2 |
2,058792 |
|
2 |
-1 |
-0,5 |
0,75 |
0,76177 |
|
3 |
-1 |
0 |
-0,5 |
-0,55396 |
|
4 |
-1 |
0,5 |
-1,75 |
-1,87926 |
|
5 |
-1 |
1 |
-3 |
-3,05016 |
|
6 |
-0,5 |
-1 |
2,75 |
2,826312 |
|
7 |
-0,5 |
-0,5 |
1,5 |
1,508202 |
|
8 |
-0,5 |
0 |
0,25 |
0,222947 |
|
9 |
-0,5 |
0,5 |
-1 |
-0,99078 |
|
10 |
-0,5 |
1 |
-2,25 |
-8,98046 |
|
11 |
0 |
-1 |
3,5 |
3,512607 |
|
12 |
0 |
-0,5 |
2,25 |
2,291399 |
|
13 |
0 |
0 |
1 |
1,056154 |
|
14 |
0 |
0,5 |
-0,25 |
-23,5889 |
|
15 |
0 |
1 |
-1,5 |
-1,52593 |
|
16 |
0,5 |
-1 |
4,25 |
4,173192 |
|
17 |
0,5 |
-0,5 |
3 |
2,972698 |
|
18 |
0,5 |
0 |
1,75 |
2,591118 |
|
19 |
0,5 |
0,5 |
0,5 |
0,410544 |
|
20 |
0,5 |
1 |
-0,75 |
-0,83882 |
|
21 |
1 |
-1 |
5 |
4,99475 |
|
22 |
1 |
-0,5 |
3,75 |
-15,1182 |
|
23 |
1 |
0 |
2,5 |
2,555675 |
|
24 |
1 |
0,5 |
1,25 |
1,248423 |
|
25 |
1 |
1 |
0 |
0,08719 |
Теперь
необходимо провести исследование параметра 
, результаты которого можно сравнить по величине .
|
|
|
|
|
|
|
1 |
0,983788 |
1,503679 |
-2,54183 |
0,002026 |
|
1,25 |
0,981218 |
1,50941 |
-2,54089 |
0,002113 |
|
1,5 |
0,979197 |
1,5109 |
-2,53947 |
0,00211 |
|
1,75 |
0,977883 |
1,512933 |
-2,54005 |
0,00226 |
|
2 |
0,976503 |
1,512933 |
-2,54143 |
0,002436 |
|
2,25 |
0,975226 |
1,512933 |
-2,54271 |
0,002605 |
|
2,5 |
0,97404 |
1,512933 |
-2,54389 |
0,002768 |
|
2,75 |
0,972935 |
1,512933 |
-2,545 |
0,002924 |
|
3 |
0,967911 |
1,512933 |
-2,55002 |
0,003699 |
|
3,25 |
0,965917 |
1,512933 |
-2,55201 |
0,004034 |
|
3,5 |
0,964082 |
1,512933 |
-2,55385 |
0,004357 |
|
3,75 |
0,961929 |
1,512933 |
-2,556 |
0,004753 |
|
4 |
0,955855 |
1,512933 |
-2,56208 |
0,00597 |
|
4,35 |
0,950015 |
1,512933 |
-2,56792 |
0,007278 |
|
4,5 |
0,587116 |
1,421141 |
-2,83902 |
0,291629 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
