










НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра прикладной математики
Дифференциальные уравнения
Группа: ПМ-12
Студент: Кичаева Н.А.
Преподаватель: Иткина Н.Б.
2003
Рассмотрим заданное уравнение двухточечной коррекции:
![]()
Выберем порядок аппроксимации, задавая различные значения коэффициентов:
По
формуле Тейлора распишем ![]()
![]()
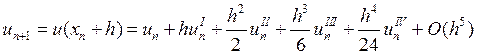
Тогда исходное уравнение будет иметь вид
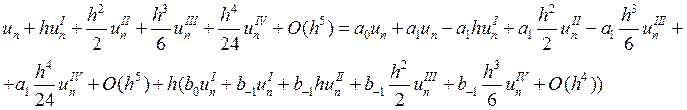
Исходя из этого уравнения, будем выписывать коэффициенты при степенях h:
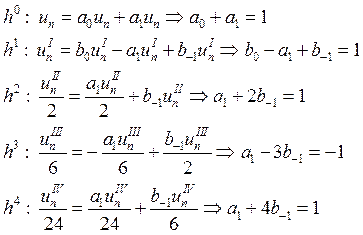
Отсюда
можно выразить все коэффициенты через ![]() .
.
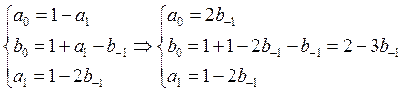
В
результате получаем семейство коррекций со вторым порядком аппроксимации:![]()
![]()
![]()
Теперь
посмотрим, как будет выглядеть коэффициент ![]() при
при ![]() :
:
Учитывая,
что ![]() получим:
получим:
![]()
Выбирая
соответственно коэффициент ![]() , мы будем получать того
или иного представителя семейства, причем имеется возможность повысить порядок
аппроксимации за счет выбора
, мы будем получать того
или иного представителя семейства, причем имеется возможность повысить порядок
аппроксимации за счет выбора 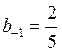 , тогда получим, что
коэффициент при
, тогда получим, что
коэффициент при ![]() обнуляется и порядок
аппроксимации становится третьим.
обнуляется и порядок
аппроксимации становится третьим.
При этом уравнение коррекции будет иметь вид:
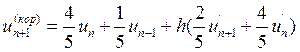 , тогда коэффициент
, тогда коэффициент ![]() при
при ![]() будет иметь вид:
будет иметь вид:
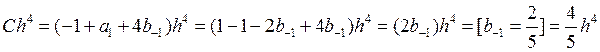
Теперь будем исследовать заданную схему коррекции на устойчивость.
Пусть
![]() - точное решение, тогда формулу для
коррекции можно записать в виде:
- точное решение, тогда формулу для
коррекции можно записать в виде:
![]()
где
![]() -погрешность, возникающая при подстановки
точного решения неточную формулу.
-погрешность, возникающая при подстановки
точного решения неточную формулу.
Пусть
теперь ![]() , т.е.разностное уравнение для вычисления
погрешности имеет вид:
, т.е.разностное уравнение для вычисления
погрешности имеет вид:
![]()
По
теореме о среднем имеем: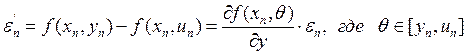
Ввиду
малости шага интегрирования h, предполагаем, что 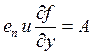 -постоянны , поэтому уравнение для
вычисления погрешности можно переписать в виде:
-постоянны , поэтому уравнение для
вычисления погрешности можно переписать в виде:
![]()
![]()
Из уравнения видно, что выбор шага может
скомпенсировать влияние коэффициента устойчивости А. Будем предполагать, что
погрешность растет как степенная функция, т.е. ![]() . Тогда предыдущее
уравнение можно переписать в виде:
. Тогда предыдущее
уравнение можно переписать в виде:
![]()
Согласно
общему определению устойчивости, общее решение однородного разностного
уравнения ![]() устойчиво , если
устойчиво , если ![]() и
условно устойчиво, если
и
условно устойчиво, если ![]() .
.
Теперь,
исходя из того, что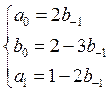 определим пределы изменения
коэффициента
определим пределы изменения
коэффициента ![]() так, чтобы схема была устойчива.
так, чтобы схема была устойчива.
![]()
![]()
Найдем корни этого уравнения.
![]()
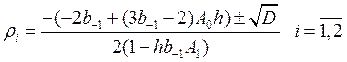
Исследуем на асимптотическую устойчивость, т.е. при ![]() , получим уравнение
, получим уравнение
![]() и его корни соответственно:
и его корни соответственно:
![]()
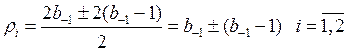
![]()
Таким образом, уже видно, что в данном случае речь может идти только об условной устойчивости:
![]()
![]()
Теперь, пытаясь подобрать подходящий прогноз для заданной коррекции, рассмотрим уравновешенную схему вида:
![]()
Проведем исследования этой схемы на порядок аппроксимации и устойчивость аналогично тому, как это было сделано для коррекции.
![]()
Определимся с порядком аппроксимации данной схемы. Используя формулу Тейлора, получим:
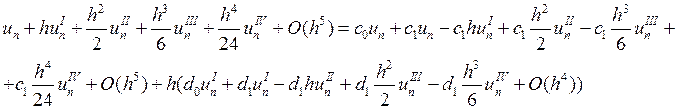
Будем выписывать коэффициенты при степенях h:
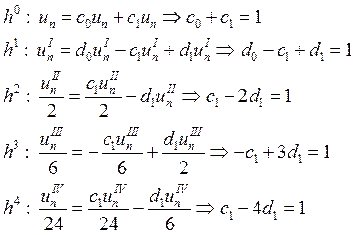
Выразим все коэффициенты через ![]() .
.
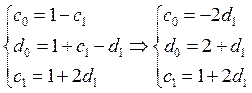
В результате получаем семейство прогнозов со вторым
порядком аппроксимации:![]()
![]()
![]()
Теперь посмотрим, как будет выглядеть коэффициент ![]() при
при ![]() :
:
Учитывая, что ![]() получим:
получим:
![]()
Выбирая аналогично, как и прошлый раз, коэффициент ![]() , мы будем получать того или иного представителя
семейства, причем имеется возможность повысить порядок аппроксимации за счет
выбора
, мы будем получать того или иного представителя
семейства, причем имеется возможность повысить порядок аппроксимации за счет
выбора ![]() , тогда получим, что коэффициент при
, тогда получим, что коэффициент при ![]() обнуляется и порядок аппроксимации становится
третьим.
обнуляется и порядок аппроксимации становится
третьим.
При этом уравнение прогноза будет иметь вид:
![]() , тогда коэффициент
, тогда коэффициент ![]() при
при ![]() будет иметь вид:
будет иметь вид:
![]()
Исследуем прогноз на устойчивость.
Если ![]() - точное решение, тогда:
- точное решение, тогда:
![]()
Если ![]() , то уравнение имеет вид:
, то уравнение имеет вид:
![]()
![]()
![]()
Будем предполагать, что погрешность растет как
степенная функция, т.е. ![]() . Тогда уравнение можно переписать в виде:
. Тогда уравнение можно переписать в виде:
![]()
Исходя из того,
что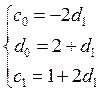 определим пределы изменения коэффициента
определим пределы изменения коэффициента ![]() так, чтобы схема была устойчива.
так, чтобы схема была устойчива.
![]()
Найдем корни этого уравнения.
![]()
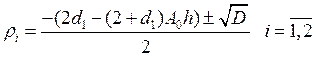
Исследуем
на асимптотическую устойчивость, т.е. при ![]() ,
получим уравнение
,
получим уравнение
![]() и его корни соответственно:
и его корни соответственно:
![]()
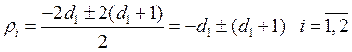
![]()
Таким образом, уже видно, что в данном случае речь может идти только об условной устойчивости:
![]()
![]()
Таким образом, зная порядок аппроксимации и область условной асимптотической устойчивости, попытаемся подобрать наилучшую пару прогноз- коррекция.
Будем рассматривать 4 пары схем прогноз-коррекция:
1.Для начала посмотрим прогноз и коррекцию на максимальном порядке аппроксимации, т.е.
![]()
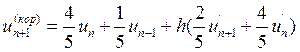
В этом случае для прогноза коэффициент ![]() при
при ![]() будет иметь вид:
будет иметь вид:
![]() , а для коррекции
, а для коррекции 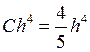 . Таким образом, прогноз оказался неустойчивым, а
коррекция устойчивой. Пара пригодна для вычислений и приближает решение с
разных сторон.
. Таким образом, прогноз оказался неустойчивым, а
коррекция устойчивой. Пара пригодна для вычислений и приближает решение с
разных сторон.
2.Затем будем рассматривать пару прогноз-коррекция второго порядка аппроксимации, выбирая коэффициенты таким, образом, чтобы коррекция и прогноз были устойчивы.
Формула прогноза второго порядка аппроксимации имеет вид:
![]() Коэффициент
Коэффициент ![]() при
при ![]() имеет вид:
имеет вид:
![]() , кроме того потребуем, чтобы прогноз был устойчив,
т.е. согласно выводам, сделанным выше необходимо, чтобы
, кроме того потребуем, чтобы прогноз был устойчив,
т.е. согласно выводам, сделанным выше необходимо, чтобы ![]() . Аналогично имеем для коррекции
. Аналогично имеем для коррекции ![]() :
:
![]() и также
и также ![]() . Отсюда, исходя из необходимости приближать решение
на каждом шаге с разных сторон, потребуем чтобы:
. Отсюда, исходя из необходимости приближать решение
на каждом шаге с разных сторон, потребуем чтобы: ![]() и, учитывая требования устойчивости имеем:
и, учитывая требования устойчивости имеем: 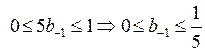 . Таким образом, выбрав
. Таким образом, выбрав 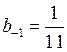 , получим, что
, получим, что 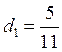 , следовательно, обе схемы при таком выборе будут
устойчивы, и коэффициенты будут иметь вид:
, следовательно, обе схемы при таком выборе будут
устойчивы, и коэффициенты будут иметь вид:
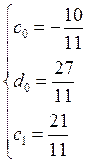 Само уравнение прогноза:
Само уравнение прогноза: 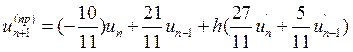 .
.
И к нему 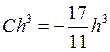
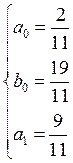 Само уравнение коррекции:
Само уравнение коррекции: 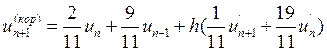 и
и 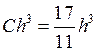 .
.
3.
Затем, продолжая
рассматривать пару двухточечных прогноза и коррекции со вторым порядком
аппроксимации, удалив требование устойчивости для прогноза, тогда выберем
следующие коэффициенты: 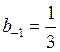 ,
, 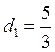 тогда
тогда 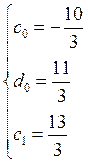 и
и 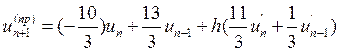 ,
,
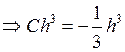 , тоже для коррекции:
, тоже для коррекции: 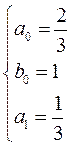 ,
,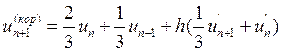
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.