4. Теперь, в поисках лучшей пары, рассмотрим сочетание: коррекция с третьим порядком аппроксимации и выше рассмотренный неустойчивый прогноз со вторым порядком аппроксимации, т.е.
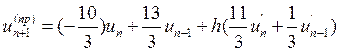 и
и 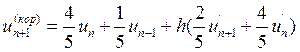 .
.
Таблицы, приведенные в отчете, делались на следующих тестах:
1.![]()
Решение ДУ имеет вид: ![]()
2.![]()
Решение ДУ имеет вид: ![]()
3.![]()
Решение ДУ имеет вид: 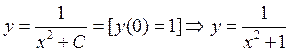 .
.
Выводы:
Рассматривая прогноз и коррекцию в каждой схеме, определим поведение погрешности и возможности аппроксимации решения для каждой из схем.
Для первой пары прогноз-коррекция с максимальным –
третьим порядком аппроксимации имеем оценку локальной погрешности аппроксимации:
![]()
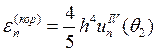 при
при
![]() . Разность между исправленным и предсказанным
значением равна:
. Разность между исправленным и предсказанным
значением равна: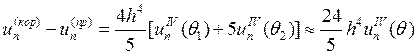
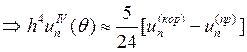 .
.
Аналогично исследуя остальные схемы, получим следующие соотношения:
2. 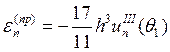
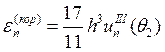
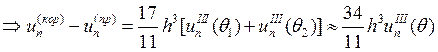
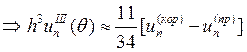
3. 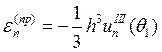
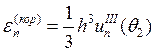
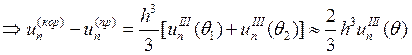
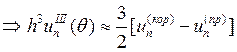
4. 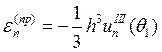
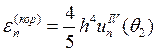
Из выше приведенных оценок можно судить о погрешности аппроксимации каждой из пар прогноз-коррекция. Теоретически, при условии, что погрешность велика, для пары с третьим порядком аппроксимации уменьшение шага h в 2 раза дает уменьшение погрешности 16 раз.
Практически же, пара с третьим порядком аппроксимации дает не более 7 верных знаков.
Наилучшей схемой среди рассмотренных, оказалась схема с неустойчивым прогнозом второго порядка и коррекцией третьего порядка аппроксимации. Она в лучшем случае дает 8 верных знаков.
Практический анализ порядка аппроксимации также не совпал с теоретическим, и вопреки теории показывает примерно одинаковую ситуацию для всех рассмотренных пар. (См. таблицу “Оценка порядка аппроксимации”).
Поскольку требование наилучшей аппроксимации решения не
является определяющим при подборе коэффициентов выбранной схемы, следует также
позаботится о ее устойчивости и как следствие о том, чтобы ошибка приближения
не превосходила и само решение. Отсюда и ограничения, накладываемые на корни соответствующего
характеристического уравнения ![]() (причем, среди
(причем, среди ![]() не должно быть кратных). Исходя из выше изложенного,
можно сказать, что требование устойчивости при подборе коррекции необходимо.
Что же касается прогноза, то требование устойчивости слишком завышено,
поскольку коррекция, выполняя свои функции, может сгладить неточности прогноза.
Если решение возрастает (тест №1), то погрешность, которая растет с такой же
скоростью или медленнее не обязательно испортит решение. И соответственно для
строго убывающего решения (тест №2,3), погрешность должна убывать с такой или
большей скоростью. В нашем случае 2 пары прогноз-коррекция второго порядка
аппроксимации наглядно демонстрируют это утверждение. Пара №3 хотя и имеет неустойчивый
прогноз, но демонстрирует чуть-чуть лучшее приближение решения, чем пара №2 с
устойчивым прогнозом. Отсюда можно сделать вывод, что свойства схемы зависят
целиком от работы прогноза и коррекции в паре.
не должно быть кратных). Исходя из выше изложенного,
можно сказать, что требование устойчивости при подборе коррекции необходимо.
Что же касается прогноза, то требование устойчивости слишком завышено,
поскольку коррекция, выполняя свои функции, может сгладить неточности прогноза.
Если решение возрастает (тест №1), то погрешность, которая растет с такой же
скоростью или медленнее не обязательно испортит решение. И соответственно для
строго убывающего решения (тест №2,3), погрешность должна убывать с такой или
большей скоростью. В нашем случае 2 пары прогноз-коррекция второго порядка
аппроксимации наглядно демонстрируют это утверждение. Пара №3 хотя и имеет неустойчивый
прогноз, но демонстрирует чуть-чуть лучшее приближение решения, чем пара №2 с
устойчивым прогнозом. Отсюда можно сделать вывод, что свойства схемы зависят
целиком от работы прогноза и коррекции в паре.
К тому же, как видно из таблиц и графиков, схема, для
которой погрешность аппроксимации, т.е.![]() ,
которая ведет себя также как само решение, лучше всего аппроксимирует задачу.
Исходя из полученных результатов можно заключить, что наилучшей схемой
оказалась схема : второго порядка аппроксимации неустойчивый прогноз и
коррекция третьего порядка аппроксимации. Эта пара лучше всего приближает
решение исходных задач. Как следует из графиков, самая худшая пара: устойчивый
прогноз- коррекция второго порядка, она дает из рассмотренных пар минимальное
число верных знаков и поведение погрешности аппроксимации ярко свидетельствует
о небольших возможностях схемы.
,
которая ведет себя также как само решение, лучше всего аппроксимирует задачу.
Исходя из полученных результатов можно заключить, что наилучшей схемой
оказалась схема : второго порядка аппроксимации неустойчивый прогноз и
коррекция третьего порядка аппроксимации. Эта пара лучше всего приближает
решение исходных задач. Как следует из графиков, самая худшая пара: устойчивый
прогноз- коррекция второго порядка, она дает из рассмотренных пар минимальное
число верных знаков и поведение погрешности аппроксимации ярко свидетельствует
о небольших возможностях схемы.
Из графиков следует, что хуже всего из рассмотренных, оказался третий тест. Поведение погрешности всех схем показывает явно “плохие” возможности аппроксимации теста №3.
Тесты №1,2 ввиду гладкости экспоненты с помощью
приближения в двух точках аппроксимируется с ошибкой порядка ![]() для лучшей из рассмотренных пар , в то
время как тест №3 из-за “нехватки” точек приближения самое лучшее
аппроксимируется с ошибкой порядка
для лучшей из рассмотренных пар , в то
время как тест №3 из-за “нехватки” точек приближения самое лучшее
аппроксимируется с ошибкой порядка ![]() .
.
2.
![]()
Найдем порядок аппроксимации схемы. Используя формулу Тейлора, получим:
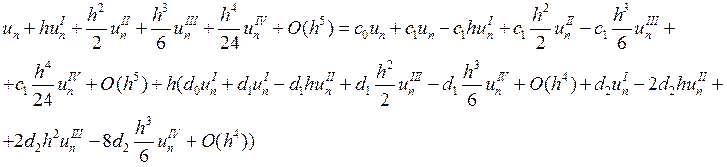
Выпишем коэффициенты при степенях h:
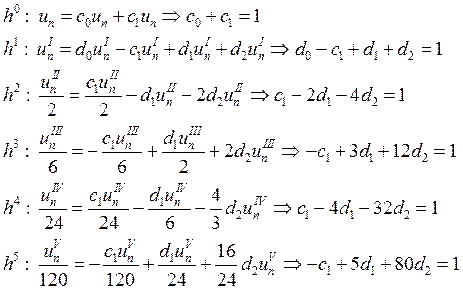
Выразим
все коэффициенты через ![]() и
и ![]() .
.
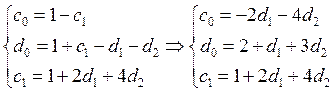
В
результате получаем семейство коррекций Адамса - Башфорта со вторым порядком
аппроксимации:![]()
![]()
![]()
Теперь
посмотрим, как будет выглядеть коэффициент ![]() при
при ![]() :
:
Учитывая,
что ![]() получим:
получим:
![]()
Можно
повысить порядок аппроксимации, если ![]() , тогда получим, что
коэффициент при
, тогда получим, что
коэффициент при ![]() обнуляется и порядок
аппроксимации становится третьим.
обнуляется и порядок
аппроксимации становится третьим.
Поскольку
теперь ![]() , то коэффициенты уравнения прогноза будут
иметь вид:
, то коэффициенты уравнения прогноза будут
иметь вид:
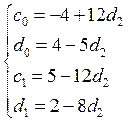 Само уравнение можно переписать в виде:
Само уравнение можно переписать в виде:
![]()
Тогда
коэффициент ![]() при
при ![]() будет
иметь вид:
будет
иметь вид:
![]()
Можно
также за счет обнуления коэффициента при ![]() добиться
получения четвертого порядка аппроксимации, но данный шаг не имеет смысла,
поскольку наивысший порядок аппроксимации данной нам коррекции – третий.
добиться
получения четвертого порядка аппроксимации, но данный шаг не имеет смысла,
поскольку наивысший порядок аппроксимации данной нам коррекции – третий.
Будем исследовать прогноз Адамса – Башфорта на устойчивость.
Если
![]() - точное решение, тогда:
- точное решение, тогда:
![]()
Если
![]() , то уравнение имеет вид:
, то уравнение имеет вид:
![]()
![]()
![]()
Будем
предполагать, что погрешность растет как степенная функция, т.е. ![]() . Тогда уравнение можно переписать в виде:
. Тогда уравнение можно переписать в виде:
![]()
Будем
рассматривать только асимптотическую устойчивость ввиду сложности уравнения,
т.е. устремим ![]() и получим:
и получим:
![]()
![]()
Найдем корни этого уравнения.
![]()
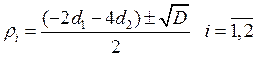
![]()
Таким образом, уже видно, что в данном случае речь может идти только об условной устойчивости:
![]()
![]()
Соответственно,
если повышать порядок аппроксимации, то ![]() и
тогда
и
тогда
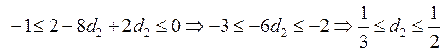
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.