Теория математического моделирования физических процессов. Нелинейная колебательная система., страница 2

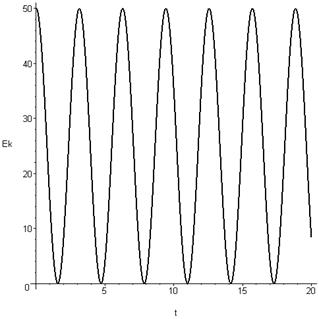
Ø  диаграмма кинетической энергии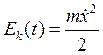. Кинетическая энергия является квадратичной функцией скорости. Величина  определяет амплитуду колебаний, которая увеличивается с ростом начальной скорости. Если рассматривать полную энергию системы, то видно, что в процессе колебаний происходит трансформация кинетической энергии в потенциальную. Энергия системы сохраняется, т.к. система является консервативной.

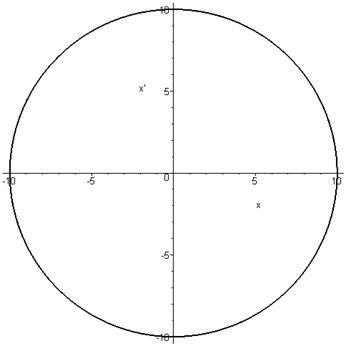
Ø  фазовый портрет на плоскости

зная решение дифференциального уравнения гармонического осциллятора можно найти уравнение траектории на фазовой плоскости.  Уравнения ,    являются параметрическими уравнениями фазовой траектории, а координатное уравнение траектории  принадлежит семейству окружностей (в общем случае эллипсов). Каждому начальному условию соответствует своя окружность. Начало координат – состояние равновесия. Рост начальной скорости влияет на диаметр окружности.

5.2. Рассмотрели случай :

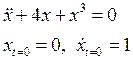
Ø  график зависимости координаты от времени

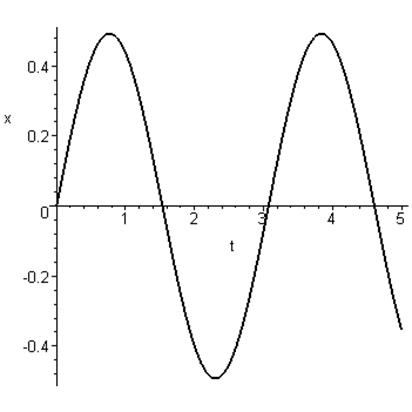
Ø  диаграмма потенциальной энергии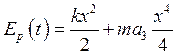

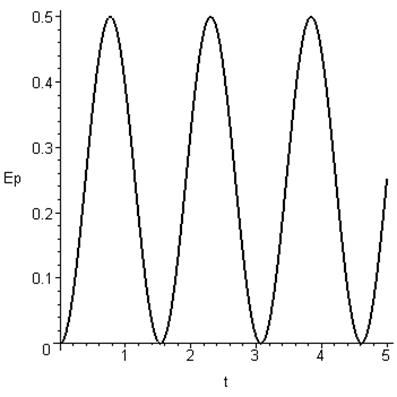
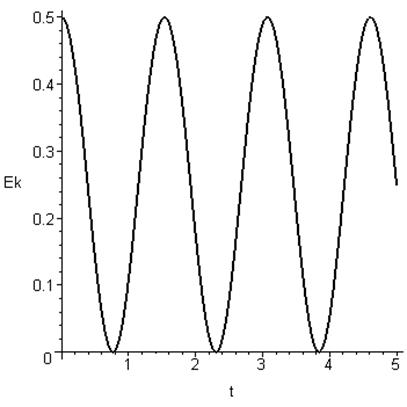
Ø  диаграмма кинетической энергии.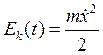

Ø  фазовый портрет на плоскости

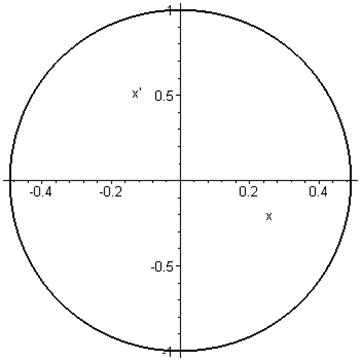
5.3.  Рассмотрели случай :

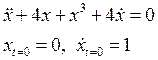
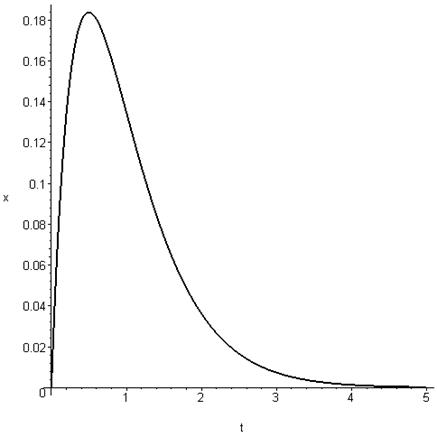
Ø  график зависимости координаты от времени

Ø  диаграмма потенциальной энергии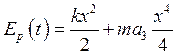

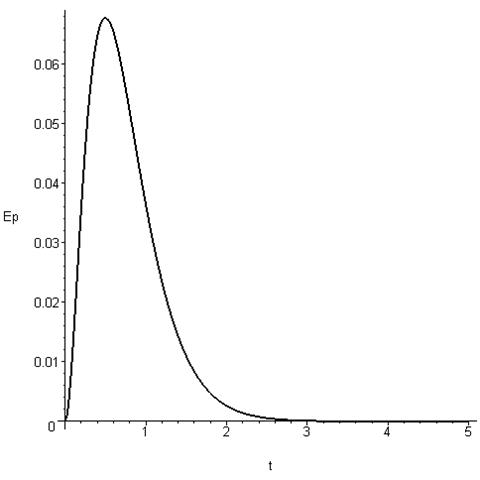
Ø  диаграмма кинетической энергии.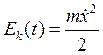

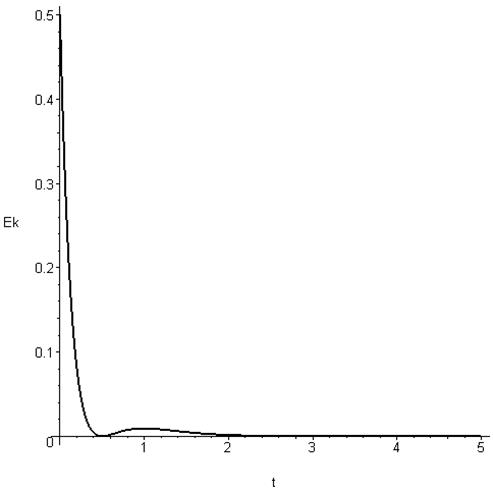
Ø  фазовый портрет на плоскости

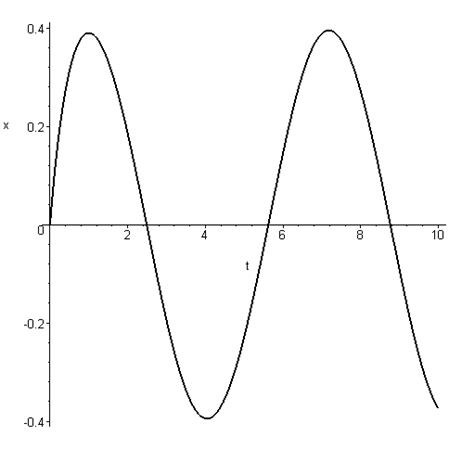
5.4.  Построили полное решение данного уравнения:

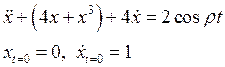
Ø  график зависимости координаты от времени

Ø  диаграмма потенциальной энергии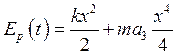

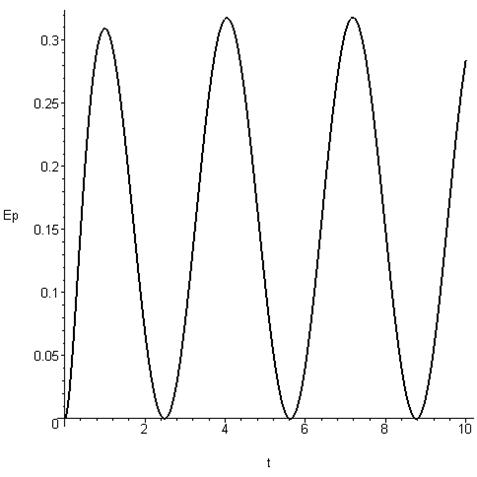
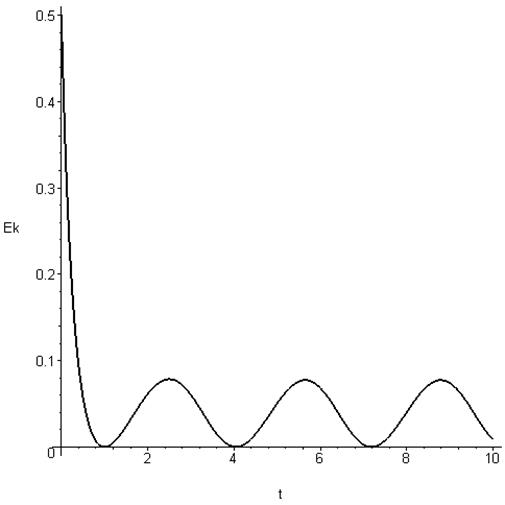
Ø  диаграмма кинетической энергии.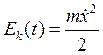

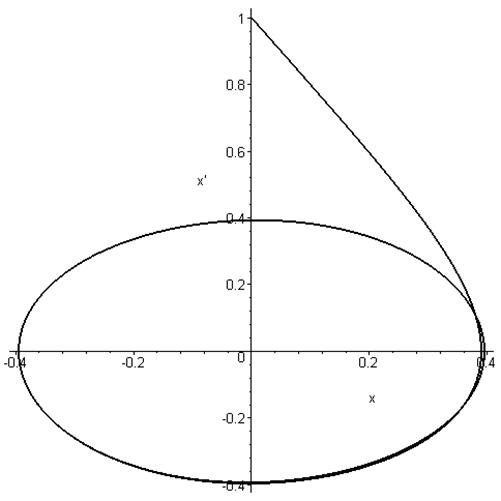
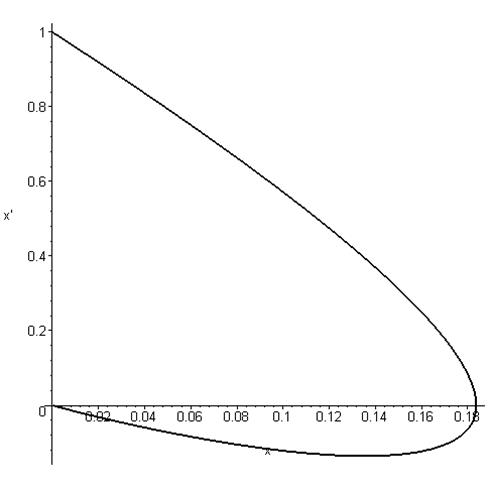
Ø  фазовый портрет на плоскости

5.5.  Для данного уравнения при  построили решение, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы:

Ø  график зависимости координаты от времени

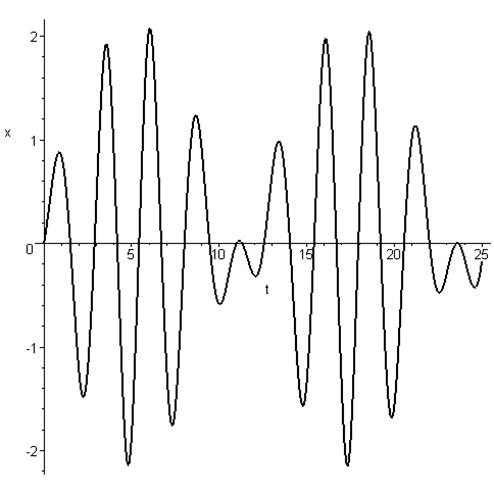
Ø  диаграмма потенциальной энергии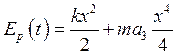

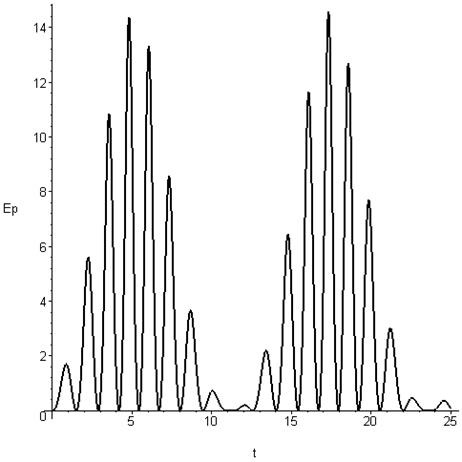
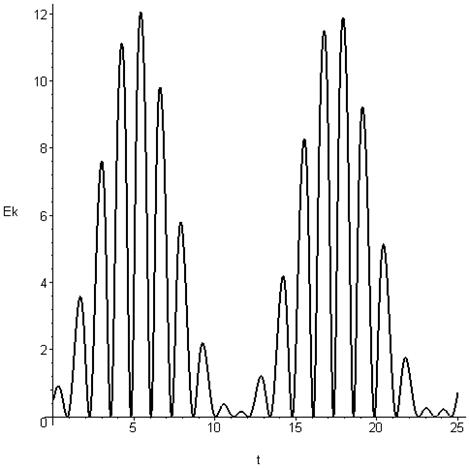
Ø  диаграмма кинетической энергии.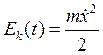

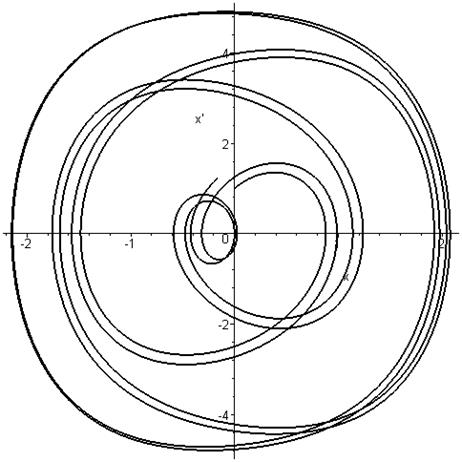
Ø  фазовый портрет на плоскости

Ø  резонансная кривая :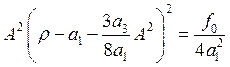

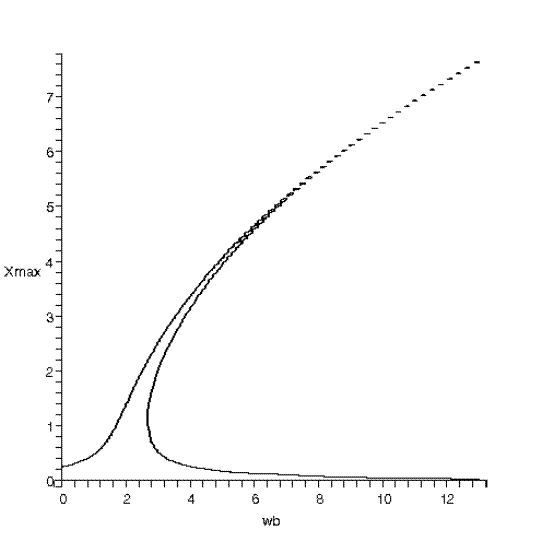
5.6.  Для случая 5.5. изучили устойчивость решений относительно малых вариаций начальных данных:

5.7.  Для полного  уравнения построили решение, положив частоту вынужденных колебаний равной частоте собственных линейных колебаний системы:

Ø  график зависимости координаты от времени

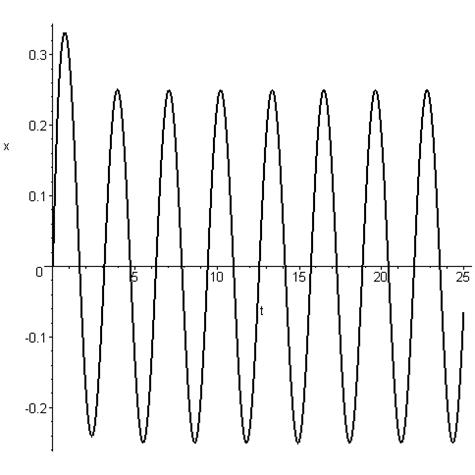
Ø  диаграмма потенциальной энергии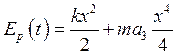

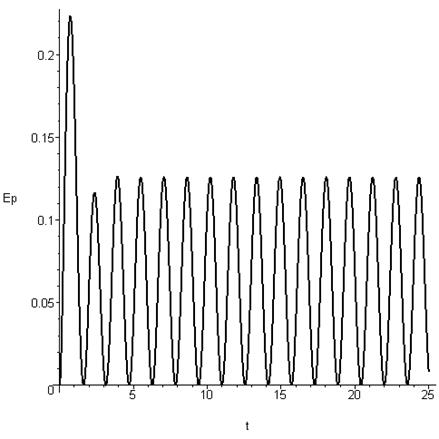
Ø  диаграмма кинетической энергии.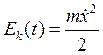

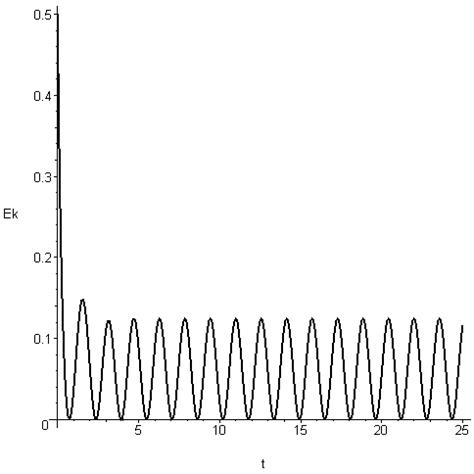
Ø  фазовый портрет на плоскости

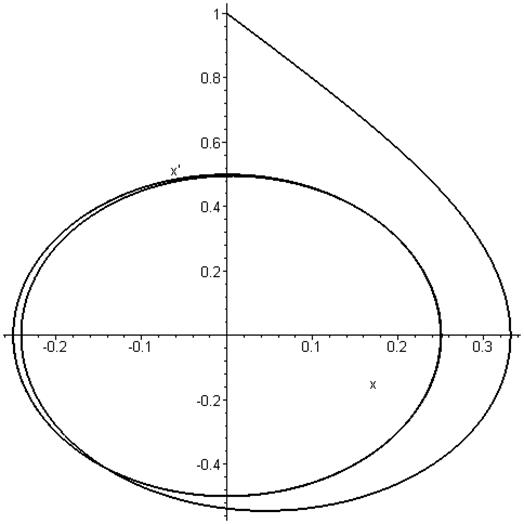
Ø  резонансная кривая :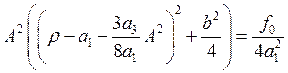

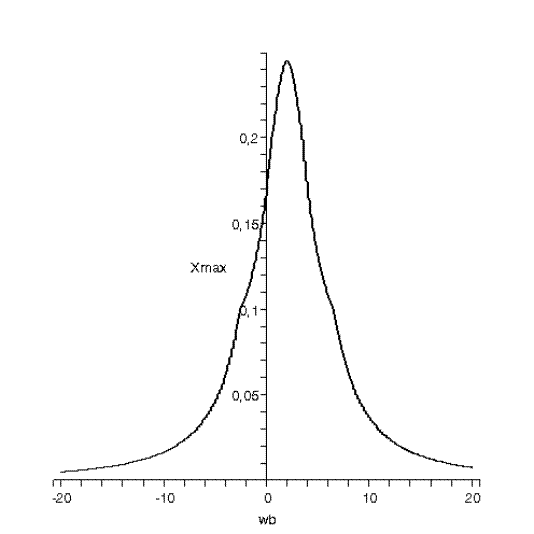
5.8.  Определили при каком условии в данном уравнении появляется субгармонический резонанс, построили соответственное численное решение для случая, когда  и :

Субгармонический резонанс появляется при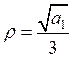

Ø  график зависимости координаты от времени:

                                                                        

        

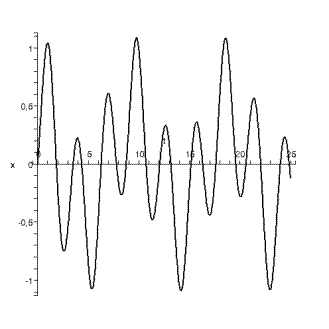
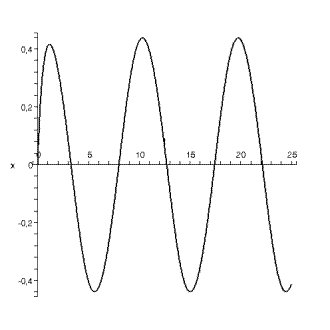
Ø  диаграмма потенциальной энергии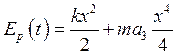

                                                                       

      

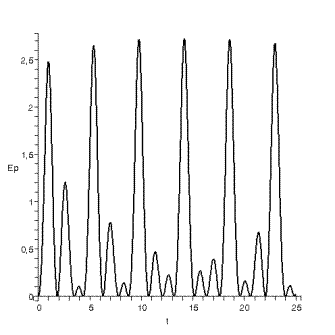
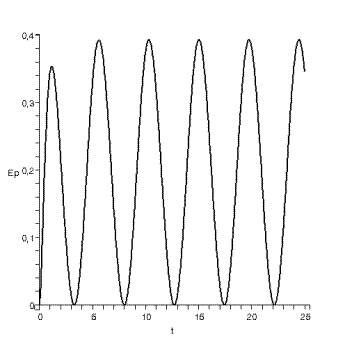
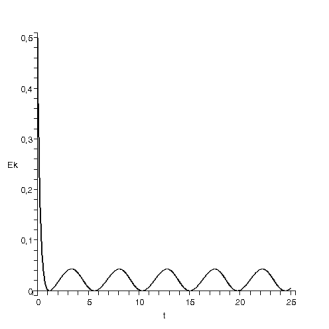
Ø  диаграмма кинетической энергии.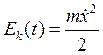

                                                                       

      

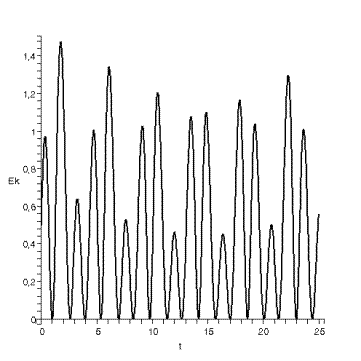
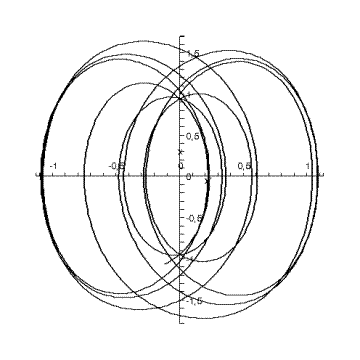
Ø  фазовый портрет на плоскости

                                                                       

   

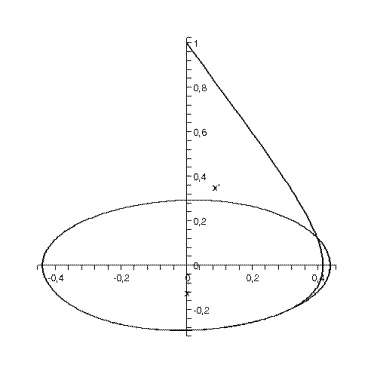
5.9.  Определили когда в данном уравнении может возникнуть параметрический резонанс, построили соответственное численное решение для случая, когда  и :

Если выбрать вынуждающую силу на утроенной частоте линейного осциллятора, то получим параметрический резонанс:

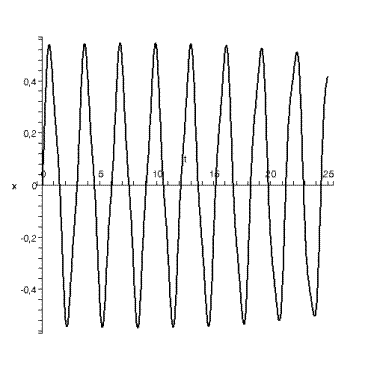
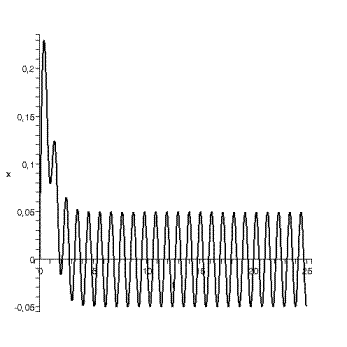
Ø  график зависимости координаты от времени:

                                                                       

         

Ø  диаграмма потенциальной энергии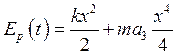

                                                                        

       

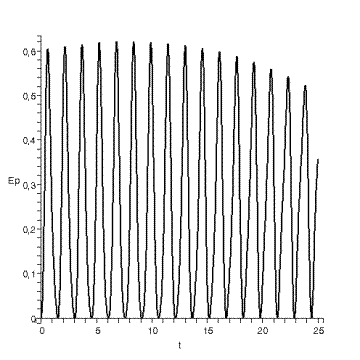
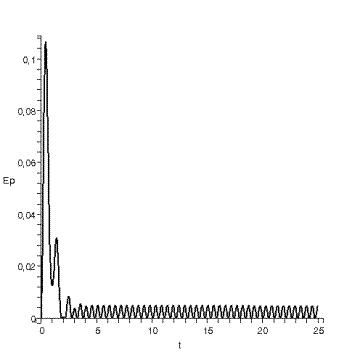
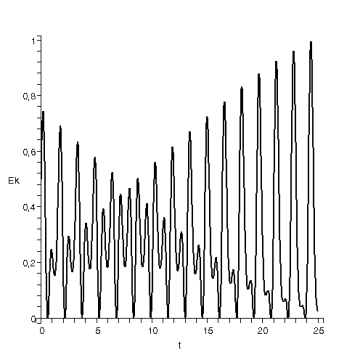
диаграмма кинетической энергии.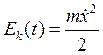

                                                                       

 

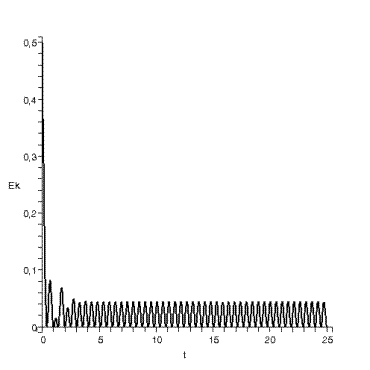
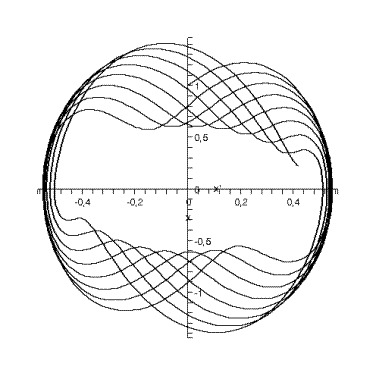
Ø  фазовый портрет на плоскости