Теория математического моделирования физических процессов. Нелинейная колебательная система.

Министерство образования Российской Федерации

Новосибирский Государственный Технический Университет

кафедра прикладной математики

Лабораторная работа №1

по дисциплине:

«Теория математического моделирования

физических процессов»

факультет:        ПМИ

группа:              ПМ-03

преподаватель: Рудяк  В.Я.

студентки:         Баландина Татьяна

Радчикова Наталья вариант             II

Новосибирск

2004

Постановка задачи:

дана нелинейная колебательная система, описываемая уравнением:

,

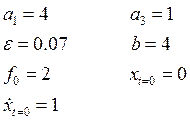
Описание метода решения: в качестве языка программирования мы выбрали Maple. Поставленные задачи мы решили с помощью оператора dsolve, который решает дифференциальные уравнения методом Рунге-Кутты пятого порядка.

Результаты расчетов в виде графиков: 

1. Определили частоту собственных линейных колебаний системы:

поскольку линейная колебательная система описывается уравнением:

, где  - частота собственных линейных колебаний, то в нашем уравнении  находится как  .

2. Исследовали линейный резонанс в системе, положив частоту вынужденных колебаний равной частоте собственных колебаний системы и :

Решение данного уравнения будем искать в виде:

, где  - разность искомого и вынужденного колебаний,  - амплитуда колебаний.

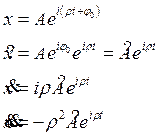
перепишем исходное уравнение в виде:

подставляя в уравнение выражения для , получим:

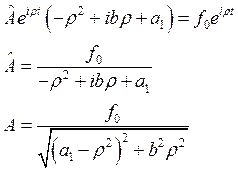
Положим частоту вынужденных колебаний равной частоте собственных колебаний системы, тогда уравнение для амплитуды примет вид:

3. Построили аналитическое решение данного уравнения, считая :

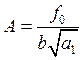
решение будем искать в виде:

, подставим это решение в уравнение:

выпишем отдельно члены при одинаковых степенях :

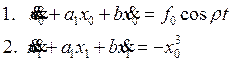
Решение первого уравнения будем искать в виде разложения в ряд Фурье:

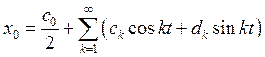
тогда

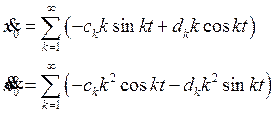
подставляя эти выражения в уравнение 1, получим:

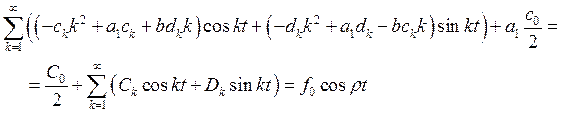
из полученного уравнения найдем :

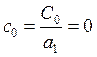
 найдем, решив систему вида:

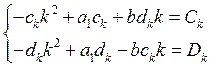
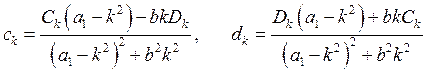
для нашего уравнения эти коэффициенты примут вид:

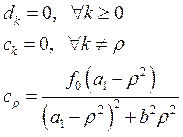
в результате получаем решение для первого уравнения:

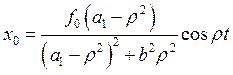
Подставляя решение первого уравнения в выражение для второго, получим:

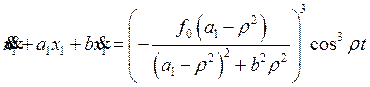
обозначим для упращения

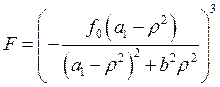
разложим  по формуле: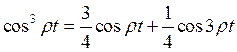 

Решение второго уравнения ищем аналогично в виде разложения в ряд Фурье:

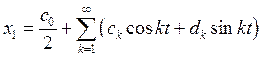
тогда

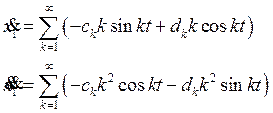
подставляя эти выражения в уравнение 2, получим:

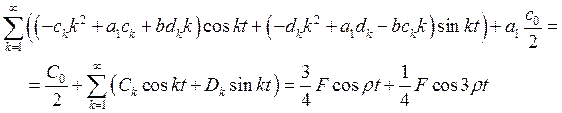
из полученного уравнения найдем :

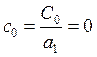
 найдем, решив систему вида:

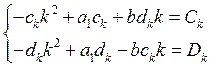
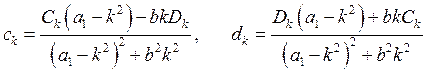
для нашего уравнения эти коэффициенты примут вид:

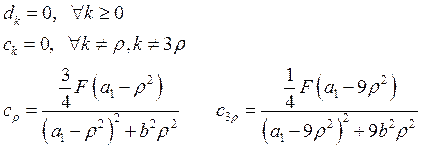
в результате получаем решение для второго уравнения:

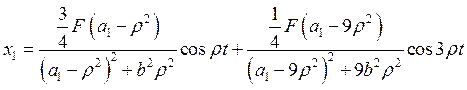
Окончательное выражение исходного уравнения:

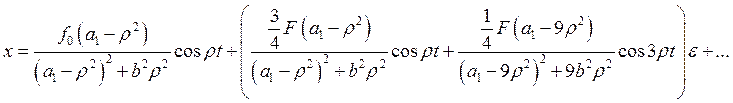, где

4. Построили аналитическое решение, соответствующее субгармоническому резонансу для случаев, когда  и :

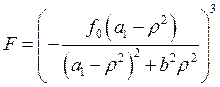
Случай, когда  :

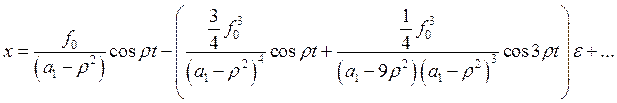
субгармонический резонанс возможен при частоте .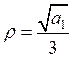

Случай, когда  :

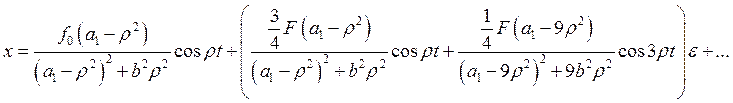, где

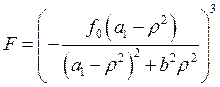
субгармонический резонанс возможен при частоте .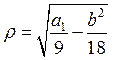

5. Построили численное решение данного уравнения:

5.1. Рассмотрели случай :

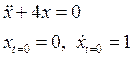
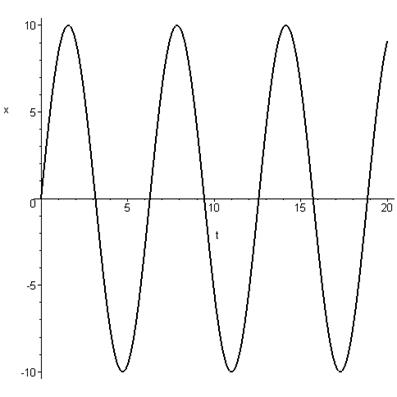
Ø  графики зависимости координаты от времени . Значение параметра А определяется начальным значением скорости. Отсюда видно, что зависимость смещения от времени можно изобразить в виде синусоиды, максимальное отклонение которой определяется начальной скоростью. Гармонический осциллятор совершает периодические синусоидальные движения. Колебательное движение не возникает лишь в случае х₀=0 и х´₀=0, т.е. когда осциллятор в начальный момент находится в состоянии равновесия. С увеличением начальной скорости растет и амплитуда.

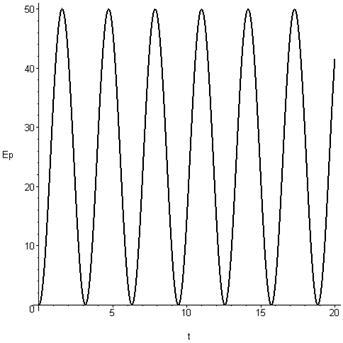
Ø  диаграмма потенциальной энергии 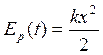 является квадратичной функцией смещения. Поскольку зависимость для смещения  имеет вид , то в данном случае максимальное отклонение кривой определяется величиной . Характер колебаний периодический. Амплитуда растет  с увеличением начальной скорости.