Теория игр. Третий алгоритм Гомори

30) Третий алгоритм Гомори.

Реализация на ЭВМ 1-го и 2-го алгоритмов Гомори может привести к неправильному результату из-за ошибок округления или ошибок при подсчёте дрбных частей .

Третий алгоритм Гомори свободен от влияния ошибок округления. Он предназначен для решения полностью целочисленной задачи линейного программирования.

;

;

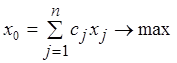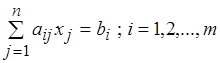; целые.

Схема 3-го алгоритма Гомори аналогична схемам, рассмотренным ранее. Отправляясь от начальной L-нормальной таблицы T₀, с помощью итераций L-метода получают последовательность таблиц T₀,T₁,…, T_s , последняя из которых является допустимой. Третий алгоритм называют ещё полностью целочисленным. Начальная таблица T₀ строится полностью целочисленная, а затем отыскивается целочисленное правильное отсечение. Дробные числа в следующей таблице получаются из-за присутствия в формулах преобразования операции деления. В этом случае целочисленность новой таблицы может быть гарантирована лишь в том случае, если разрешающий элемент будет равен (-1). Это и делается в 3-ем алгоритме Гомори при построении отсечения. Его строят так, чтобы разрешающий элемент был (-1).

Формулировка целочисленного правильного отсечения звучит следующим образом.

Пусть - недопустимая целочисленная таблица, L-нормальная. Тогда  должно удовлетворять следующим  условиям:

1.  Условие целочисленности  : r_j -целое,  "jÎN⁰.

2.  Условие отсечения : z(`x )=r₀<0 .

3.  Условие правильности. Для любого плана `x задачи (L<sup>j</sup>,C) выполняется неравенство z(`x )³0.

4.  Условие сохранения целочисленности. Если среди чисел r_j (jÎN) есть отрицательные и 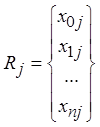 - столбец матрицы T_j (jÎN) и  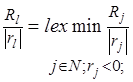, то r_l = -1.

Это значит, что если строчка z(`x ) выбирается в качестве направляющей, то направляющий элемент равен (-1).

Алгоритм определения оптимального плана можно выразить следующим образом. Начинают с походной недопустимой таблицы T₀.Затем построив правильное целочисленное отсечение, удовлетворяющее условиям 1-4, переходят к таблице T₁, затем к T₂, и т.д. пока не получат допустимую таблицу. Как и прежде используются итерации L-метода, ограничения, полученные из сформулированного отсечения приписываются снизу к соответствующей таблице. Вся последовательность таблиц, формируемая в процессе решения, является целочисленной и L-нормальной.

3-ий алгоритм Гомори.

x₀= x₁ + x₂ ®max

x₁ + x₂ + x₃ =9

-4x₁ +7 x₂ + x₄ =4

5x₁ -6 x₂ + x₅ =6 .

x_j ³ 0, целое.

L – нормальная , недопустимая таблица.

h(3)=0, h(2)=1, l=2, h(3)<h(2), l= - x_kl =11,

.

Остальные x_kj ³0, Þl= - x_kl = 7.

.

l=5, .

l=3,

План допустим.

Доказательство конечности третьего алгоритма Гомори.

Пусть задана полностью целочисленная задача линейного программирования  и ее условия определяются целочисленной l-нормальной таблицей T₀.

Теорема. Если существует план  задачи , то третий алгоритм Гомори конечен.

                 

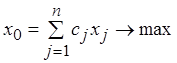
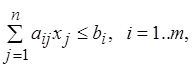
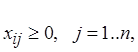
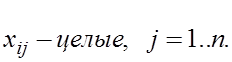
Доказательство: По прежнему обозначаем симплексную таблицу на p-м шаге:

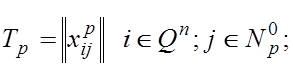 где N_p – множество индексов              небазисных переменных.

 - расширенный l-псевдоплан, соответствующий таблице T_r.

Далее, пусть . Обозначим через  номер направляющего столца на p-й итерации:

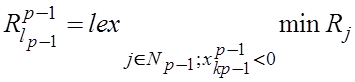
Очевидно, что в силу правил l-метода:

         (1)

Отсюда следует, что

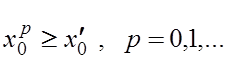            (2)

Далее, существует такое p₀ , что

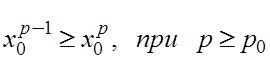         (3)

Это, действительно, так, потому что  - целое при любом p, а следовательно, целое и

А это значит, что количество итераций p , для котрых

не превышает , отсюда и следует (3) (т.к. на каждой итерации x₀ меняется).

Допустим теперь, что количество итераций бесконечно. Тогда найдутся такие α₁³1 и p₁³1, что

1) 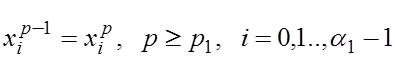 (4) – i-тые компоненты перестают меняться.

2) Найдется сколь угодно  большое p, для которого:

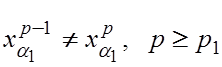                                                                                     (5)

Из (1),(4) и (5) имеем:

.                                                                                                  (6)

Следовательно, найдется такое p₁³p₂ , что

                                                                      (7)

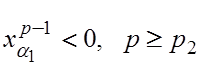                                                                                          (8)

Рассмотрим q-ю итерацию при q³p₂. Из (8) следует, что:

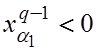                                                                                                                (9) 

                                                                                                             (10)

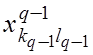а отсюда в силу отрицательности  и лексикографической положительности 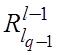 получаем :

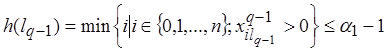                                                  (11)

Из (11) следует, что

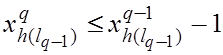, где  ,                             (12)

в силу целочисленности отсечений соответствующий элемент в новой таблице хотябы на 1 .

Сравнивая (7) и (12), получаем противоречие. Следовательно, конечность третьего алгоритва доказана.

Алгоритм Гомори (3) может оказаться не конечным, если множество планов задачи (L^j,C) пусто или пусто даже множество планов задачи(L,C). Финкельштейном предложена небольшая и естественная модификация, гарантирующая конечность при соблюдении следующих условий:

1.  Построена исходная целочисленная и и L-нормальная таблица T₀.

2.  Множество D планов  задачи (L,C) ограничено. В силу ограниченности множества D можно методами линейного программирования найти .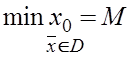

Если задача минимизации x₀  на D неразрешима, то неразрешима и задача (L^j,C).

Если же эта задача разрешима, то для любого плана задачи (L^j,C) получаем  , где ]M[ - наименьшее целое число, не меньшее M. В исходной таблице T₀ x₀ заменяется на x₀^¢ . (Компоненты исходного оптимального плана от этого не изменятся ). Теперь при проверке допустимости таблицы T_p начинают с неотрицательности числа