Схема моделирования равномерно распределенных псевдослучайных чисел. Мультипликативный генератор Лемера, страница 2

При  гипотеза о согласии с видом распределения отвергается, иначе не отвергается.

Критерий  Пирсона представлен в виде: .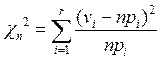

3. Моделирование непрерывных псевдослучайных величин. Найти методом обратной функции моделирующее выражение для случайной величины, имеющей заданное распределение. Реализовать алгоритм моделирования последовательности случайных величин.

Заданная плотность распределения:  экспоненциальное ,

Метод моделирование случайной непрерывной величины (метод обратной функции):

Функция распределения заданной плотности распределения: 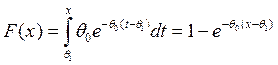. Тогда , . Отсюда моделирующая функция для : 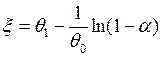. Поскольку и одинаково распределены, получим: 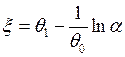, где .

Используя последовательность равномерных псевдослучайных величин, полученную в первом пункте третьем  подпункте, будем строить наши дальнейшие исследования.

Исследования:

3.1) Входные параметры

В выборке повторялось 38 набл.

Результаты оценивания параметров распределения:

Экспоненциальное с масштабом 1.0000 со сдвигом 0.0000

Метод максимального правдоподобия

Оценка по серединам интервалов

Уровень значимости (вероятность ошибки первого рода) a= 0.01   

Достигаемый уровень значимости (вероятность согласия) P=1-G(S|H0)= 0.42238

P>a: гипотеза о согласии НЕ ОТВЕРГАЕТСЯ

Результаты проверки согласия: k=7, r=0

Отношения правдоподобия S=2.2606   P=0.89423

Хи-квадрат Пирсона c попр.Никулина S=2.2389   P=0.89647

Колмогорова S=0.80066  P=0.54306

Смирнова S=2.5642   P=0.27745

Омега-малое кв. Мизеса S=0.26075  P=0.17515

Омега-большое кв. Мизеса S=1.5264   P=0.1703 

Реньи S=1e+100   P=0      

Прим.: статистика Хи-квадрат с поправкой Никулина

Наилучшее:

Эксп(0.00,1.00)

График функции распределения:

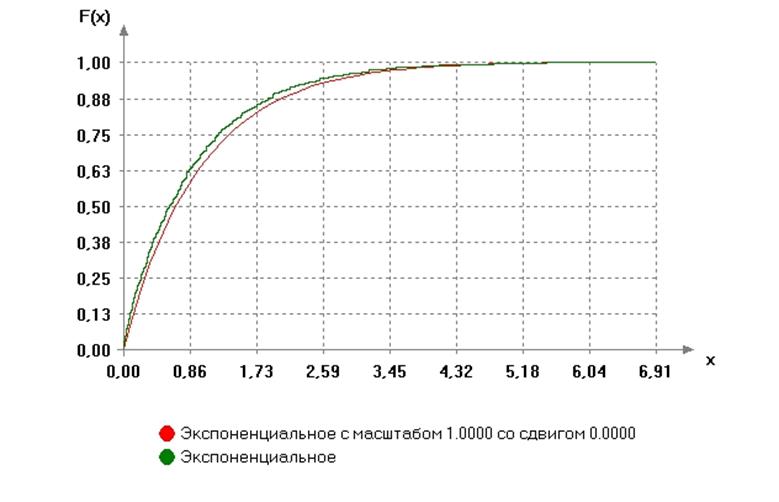
3.2) Входные параметры

В выборке повторялось 38 набл.

Результаты оценивания параметров распределения:

Экспоненциальное с масштабом 1.0000 со сдвигом 0.0000

Метод максимального правдоподобия

Оценка по серединам интервалов

Уровень значимости (вероятность ошибки первого рода) a= 0.01   

Достигаемый уровень значимости (вероятность согласия) P=1-G(S|H0)= 0.14282

P>a: гипотеза о согласии НЕ ОТВЕРГАЕТСЯ

Результаты проверки согласия: k=7, r=0

Отношения правдоподобия S=296.35   P=4.964e-61

Хи-квадрат Пирсона c попр.Никулина S=269.22   P=3.1787e-55

Колмогорова S=8.9727   P=0      

Смирнова S=0.00055556 P=0.99972

Омега-малое кв. Мизеса S=25.016   P=0      

Омега-большое кв. Мизеса S=117.07   P=0      

Реньи S=1e+100   P=0      

Прим.: статистика Хи-квадрат с поправкой Никулина

Наилучшее:

Эксп(0.00,1.00)

График функции распределения:

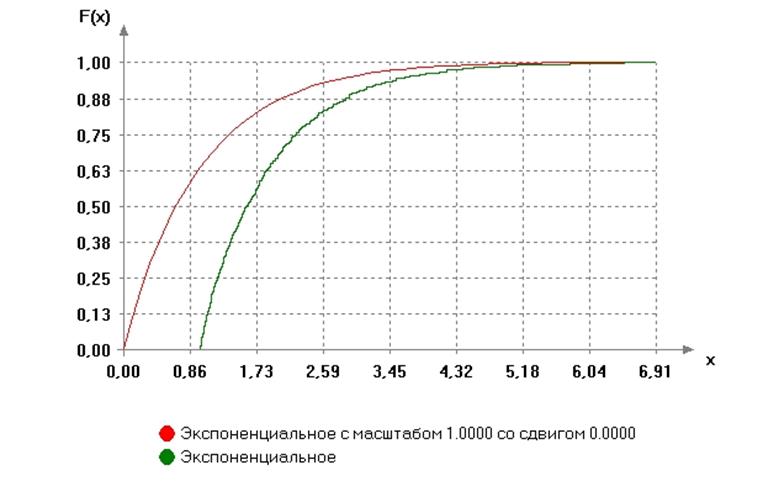
3.3) Входные параметры

В выборке повторялось 38 набл.

Результаты оценивания параметров распределения:

Экспоненциальное с масштабом 1.0000 со сдвигом 0.0000

Метод максимального правдоподобия

Оценка по серединам интервалов

Уровень значимости (вероятность ошибки первого рода) a= 0.01   

Достигаемый уровень значимости (вероятность согласия) P=1-G(S|H0)= 0.13907

P>a: гипотеза о согласии НЕ ОТВЕРГАЕТСЯ

Результаты проверки согласия: k=7, r=0

Отношения правдоподобия S=793.6    P=0      

Хи-квадрат Пирсона c попр.Никулина S=1338.3   P=0      

Колмогорова S=12.244   P=0      

Смирнова S=0.053751 P=0.97348

Омега-малое кв. Мизеса S=46.338   P=0      

Омега-большое кв. Мизеса S=259.47   P=0      

Реньи S=1e+100   P=0      

Прим.: статистика Хи-квадрат с поправкой Никулина

Наилучшее:

Эксп(0.00,1.00)

График функции распределения:

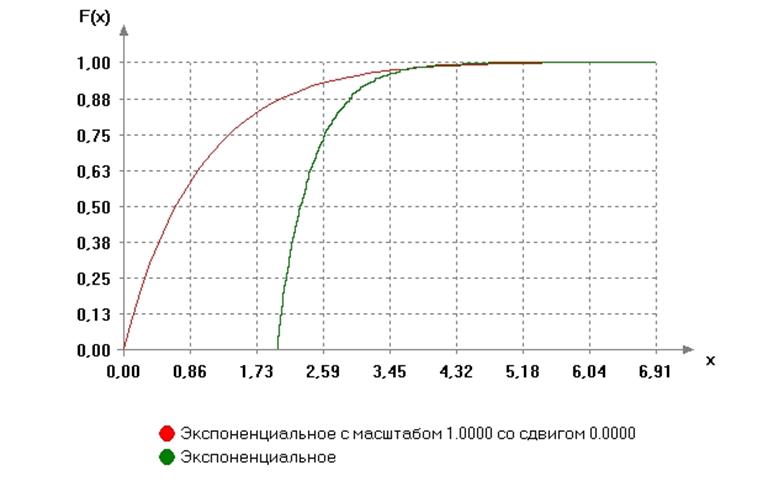
Вывод:

1. При моделировании равномерно распределенных на отрезке [0,1]        псевдослучайных чисел, значение коэффициента m нужно брать достаточно большим, чтобы значения периода сделать как можно больше. Причем период полученной последовательности не должен быть равным нулю. Х0 берем меньше значения m.

2. Оптимальными параметрами для экспоненциального распределения являются , как показали результаты.

3. Проверка гипотезы о согласи сгенерированной выборки с равномерным законом распределения с помощью программной системы ISW показала, что последовательность псевдослучайных чисел распределена равномерно.

4. Проверка гипотезы о согласии сгенерированной выборки  с экспоненциальным распределением с помощью программной системы ISW показала, что последовательность псевдослучайных чисел распределена по экспоненциальному закону.

5. Проверка гипотезы о согласии сгенерированной выборки с биномиальным распределением по критерию  Пирсона, показала, что последовательность псевдослучайных чисел распределена по биномиальному закону.

Новосибирский государственный технический университет

Кафедра Прикладной математики и Информатики

Лабораторная работа №3

по дисциплине

 «Моделирование и управление в экономике»

Факультет:            ПМИ

Группа:                  ПМ-13

Студенты:             Глухова М.А.

Преподаватели:    Чимитова Е. В.

Вариант:          №  1

Новосибирск 2005