Схема моделирования равномерно распределенных псевдослучайных чисел. Мультипликативный генератор Лемера

1. Разработать программу, реализующую соответствующую схему моделирования равномерно распределенных псевдослучайных чисел на отрезке [0,1].

Тип программного генератора моделирования псевдослучайных величин –  мультипликативный генератор Лемера: 

Образование равномерно распределенных псевдослучайных чисел на отрезке [0,1] можно представить следующим образом   .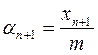

Количество элементов в сгенерированной выборке N=200.

Исследования:

1.1) Входные параметры:

Результат тестирования в программной системе ISW:

В выборке повторялось 182 набл.

Результаты оценивания параметров распределения:

Равномерное с масштабом 1.0000 со сдвигом 0.0000

Метод максимального правдоподобия

Оценка по серединам интервалов

Уровень значимости (вероятность ошибки первого рода) a= 0.01   

Достигаемый уровень значимости (вероятность согласия) P=1-G(S|H0)= 0.58055

P>a: гипотеза о согласии НЕ ОТВЕРГАЕТСЯ

Результаты проверки согласия: k=7, r=0

Отношения правдоподобия S=3.032    P=0.80482

Хи-квадрат Пирсона c попр.Никулина S=2.9653   P=0.81319

Колмогорова S=0.66128  P=0.77434

Смирнова S=1.7491   P=0.41704

Омега-малое кв. Мизеса S=0.074019 P=0.72714

Омега-большое кв. Мизеса S=0.73872  P=0.52735

Реньи S=1e+100   P=0      

Прим.: статистика Хи-квадрат с поправкой Никулина

Наилучшее:

Рав(0.00,1.00)

График функции распределения:

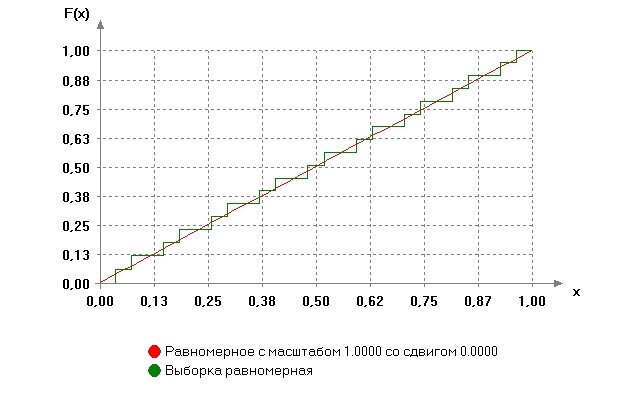
1.2) Входные параметры:

Результат тестирования в программной системе ISW:

В выборке повторялось 146 набл.

Результаты оценивания параметров распределения:

Равномерное с масштабом 1.0000 со сдвигом 0.0000

Метод максимального правдоподобия

Оценка по серединам интервалов

Уровень значимости (вероятность ошибки первого рода) a= 0.01   

Достигаемый уровень значимости (вероятность согласия) P=1-G(S|H0)= 0.77178

P>a: гипотеза о согласии НЕ ОТВЕРГАЕТСЯ

Результаты проверки согласия: k=7, r=0

Отношения правдоподобия S=0.94267  P=0.98769

Хи-квадрат Пирсона c попр.Никулина S=0.95279  P=0.98734

Колмогорова S=0.50588  P=0.96006

Смирнова S=1.0237   P=0.59939

Омега-малое кв. Мизеса S=0.043451 P=0.9146 

Омега-большое кв. Мизеса S=0.27854  P=0.95335

Реньи S=1e+100   P=0      

Прим.: статистика Хи-квадрат с поправкой Никулина

Наилучшее:

Рав(0.00,1.00)

График функции распределения:

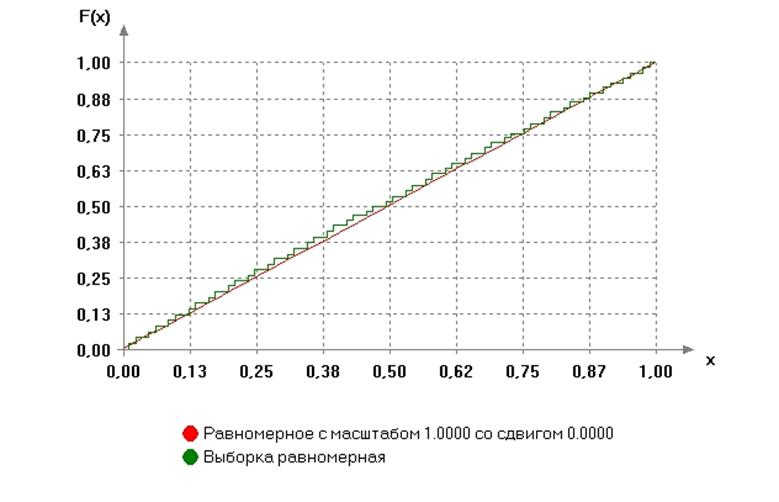
1.3) Входные параметры:

Результат тестирования в программной системе ISW:

В выборке повторялось 38 набл.

Результаты оценивания параметров распределения:

Равномерное с масштабом 1.0000 со сдвигом 0.0000

Метод максимального правдоподобия

Оценка по серединам интервалов

Уровень значимости (вероятность ошибки первого рода) a= 0.01   

Достигаемый уровень значимости (вероятность согласия) P=1-G(S|H0)= 0.39942

P>a: гипотеза о согласии НЕ ОТВЕРГАЕТСЯ

Результаты проверки согласия: k=7, r=0

Отношения правдоподобия S=2.9365   P=0.81677

Хи-квадрат Пирсона c попр.Никулина S=2.9653   P=0.81319

Колмогорова S=0.80066  P=0.54307

Смирнова S=2.5642   P=0.27745

Омега-малое кв. Мизеса S=0.26075  P=0.17515

Омега-большое кв. Мизеса S=1.5264   P=0.1703 

Реньи S=1e+100   P=0      

Прим.: статистика Хи-квадрат с поправкой Никулина

Наилучшее:

Рав(0.00,1.00)

График функции распределения:

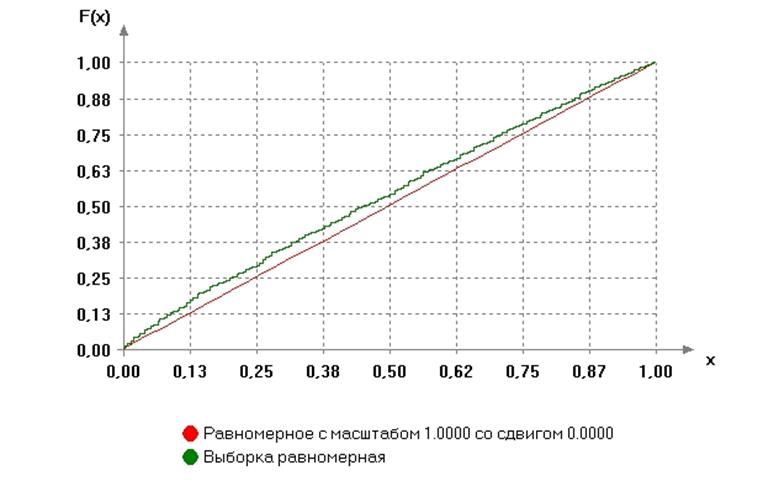
2. Моделирование дискретных псевдослучайных величин. Найти рекуррентное соотношение для вычисления вероятности . Разработать и реализовать алгоритм моделирования соответствующей псевдослучайной дискретной величины.

Тип дискретного распределения: биномиальное распределение , , .

Рекуррентное соотношение . Для этого распределения:

, .

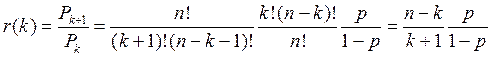Количество элементов в выборке N=200.

Уровень значимости (вероятность ошибки первого рода) .

Результаты проверки выборки по критерию  Пирсона при различных значениях входного параметра :

n	p				итог
10	0.1	3.338856	0,949333599		НЕ отвергается
	0.2	8.807527	0,45522769		НЕ отвергается
	0.3	15.919928	0,068572646		НЕ отвергается
	0.4	8.129246	0,521175752		НЕ отвергается
	0.5	6.914783	0,645991423		НЕ отвергается
	0.6	6.953838	0,641925676		НЕ отвергается
	0.7	9.969434	0,352965379		НЕ отвергается
	0.8	9.733123	0,372519377		НЕ отвергается
	0.9	3.596538	0,93590873		НЕ отвергается
20	0,10	9.315526	0,967863596		НЕ отвергается
	0,20	26.614679	0,113953427		НЕ отвергается
	0,30	24.498873	0,177706734		НЕ отвергается
	0,40	18.638905	0,480210509		НЕ отвергается
	0,50	28.655262	0,071604596		НЕ отвергается
	0,60	18.663937	0,478577293		НЕ отвергается
	0,70	23.405962	0,219933657		НЕ отвергается
	0,80	28.299685	0,07782849		НЕ отвергается
	0,90	10.194965	0,947971263		НЕ отвергается