Реализовать методы простой итерации, релаксации и метод Ньютона для задачи
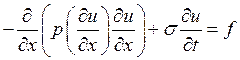
линейные базисные функции, первые и вторые краевые условия,
неявная двухслойная схема, ![]() считать постоянной на
КЭ.
считать постоянной на
КЭ.
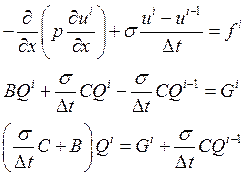
На каждом слое решаем такую СЛАУ, Q0 получаем из начального условия.
Так как задача нелинейная, то задаём начальное приближение и решаем задачу итерационно. Будем использовать релаксацию:
![]() .
.
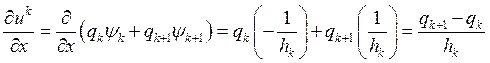 . Значит производная на k-том КЭ – константа, а значит и p
тоже. Получаем
. Значит производная на k-том КЭ – константа, а значит и p
тоже. Получаем
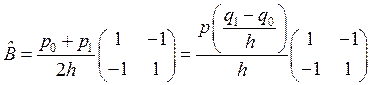
Aq=F, где 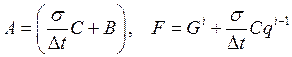 .
.
Рассмотрим один конечный элемент
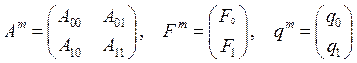
q0 – решение на предыдущей итерации
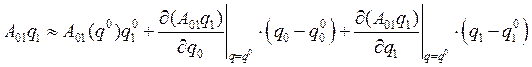
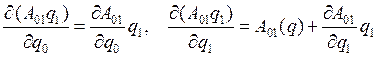
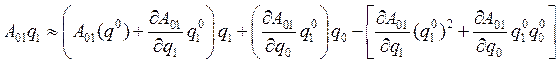
Найдём производные
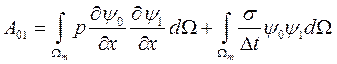
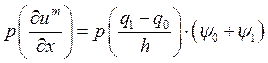
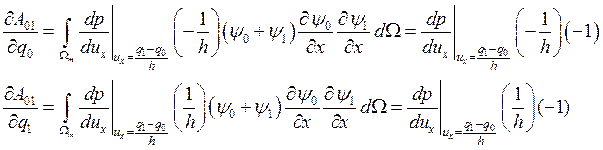
Таким образом
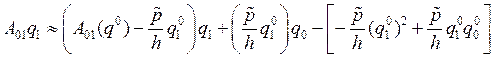 , где
, где 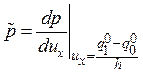
Если аналогичным образом выразить A00q0, A11q1, A10q0, то получим новую локальную матрицу
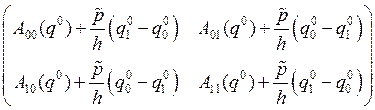
и локальный вектор правой части
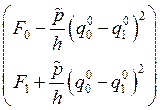
Тестирование
1) ![]()
первые краевые
|
t \ x |
1 |
2 |
3 |
4 |
5 |
|
|
2 |
1 |
0.99999994 |
1.0000001 |
0.9999999 |
1 |
7.9968022e-08 |
|
3 |
1 |
0.99999994 |
1.0000002 |
0.9999998 |
1 |
1.359195e-07 |
|
4 |
1 |
0.99999994 |
1.0000002 |
0.9999997 |
1 |
1.7275067e-07 |
|
5 |
1 |
0.99999994 |
1.0000002 |
0.9999997 |
1 |
1.7275067e-07 |
t: 1, 1.1, 1.2, 1.3, 1.4
|
t \ x |
1 |
2 |
3 |
4 |
5 |
|
|
1.1 |
1 |
1.0000001 |
1 |
1.0000001 |
1 |
7.5394571e-08 |
|
1.2 |
1 |
1.0000001 |
1 |
1.0000001 |
1 |
7.5394571e-08 |
|
1.3 |
1 |
1.0000001 |
1 |
1 |
1 |
5.3312015e-08 |
|
1.4 |
1 |
1.0000001 |
1 |
1.0000001 |
1 |
7.5394571e-08 |
первые и вторые краевые
|
t \ x |
1 |
2 |
3 |
4 |
5 |
|
|
1.1 |
1 |
1.0000001 |
1.0000001 |
1 |
1.0000001 |
9.233911e-08 |
|
1.2 |
1 |
1.0000002 |
1.0000002 |
1 |
1.0000001 |
1.5993602e-07 |
|
1.3 |
1 |
1.0000002 |
1.0000001 |
1 |
1 |
1.1920928e-07 |
|
1.4 |
1 |
1.0000001 |
1.0000002 |
1 |
1.0000001 |
1.3058722e-07 |
|
t \ x |
1 |
1.1 |
1.2 |
1.3 |
1.4 |
|
|
1.1 |
1 |
0.99999994 |
1.0000001 |
1 |
1 |
5.9604645e-08 |
|
1.2 |
1 |
0.99999994 |
1.0000002 |
0.99999988 |
1 |
1.2215317e-07 |
|
1.3 |
1 |
0.99999994 |
1.0000002 |
1 |
1 |
1.0990553e-07 |
|
1.4 |
1 |
0.99999994 |
1.0000001 |
1.0000001 |
0.99999988 |
9.6109597e-08 |
2) 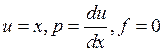 ,краевые:
вторые,первые,
,краевые:
вторые,первые,
![]()
|
t \ x |
1 |
2 |
3 |
4 |
|
|
2 |
0.99999982 |
1.9999998 |
3 |
4 |
5.4411349e-08 |
|
3 |
0.9999997 |
1.9999998 |
2.9999995 |
4 |
1.1151009e-07 |
|
4 |
0.99999958 |
1.9999995 |
3 |
4 |
1.1568012e-07 |
|
t \ x |
1 |
1.5 |
2 |
2.5 |
|
|
1.5 |
1.0000004 |
1.5000002 |
2 |
2.4999998 |
1.3377276e-07 |
|
2 |
1.0000004 |
1.5000004 |
2.0000002 |
2.4999998 |
1.6543594e-07 |
|
2.5 |
1.0000004 |
1.5000002 |
2 |
2.4999998 |
1.3377276e-07 |
![]()
|
t \ x |
1 |
1.5 |
2 |
2.5 |
|
|
1.5 |
0.99999976 |
1.4999998 |
1.9999998 |
2.4999998 |
1.2977865e-07 |
|
2 |
0.99999976 |
1.4999998 |
1.9999998 |
2.4999998 |
1.2977865e-07 |
|
2.5 |
0.99999976 |
1.4999998 |
1.9999998 |
2.4999998 |
1.2977865e-07 |
3) 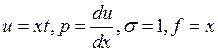
|
t \x |
1 |
2 |
3 |
4 |
|
выход |
|
2 |
2 |
4.0000005 |
6 |
8 |
4.3529078e-08 |
7.1526e-07 |
|
3 |
2.9999998 |
5.9999995 |
8.9999981 |
11.999999 |
1.3377277e-07 |
2.9005e-06 |
|
4 |
4 |
8 |
11.999999 |
16 |
4.3529078e-08 |
1.966e-06 |
2 итерации по всем слоям
4) ![]()
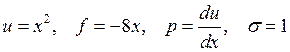
|
x=0.1 |
x=1.1 |
x=2.1 |
x=3.1 |
|
|
точное |
0.01 |
1.21 |
4.41 |
9.61 |
|
t=2 |
0.0099999998 |
1.2100004 |
4.4100003 |
9.6099997 |
|
t=3 |
0.0099999998 |
1.2100005 |
4.4099998 |
9.6099997 |
![]()
|
t=2 |
0.0099999998 |
1.2100004 |
4.4099998 |
9.6099997 |
|
t=3 |
0.0099999998 |
1.2100005 |
4.4100003 |
9.6099997 |
одна итерация
5) 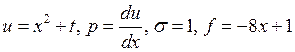
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.