




Случайный эксперимент – эксперимент, результат которого нельзя предугадать заранее.
Случайное событие – исход случайного эксперимента.
![]() называют дискретным,
если оно конечно.
называют дискретным,
если оно конечно.
Событие – любое
подмножество ![]() ; состоит из
некоторой совокупности элементарных событий; происходит, если произошло одно из
элементарных событий, содержащихся в нем.
; состоит из
некоторой совокупности элементарных событий; происходит, если произошло одно из
элементарных событий, содержащихся в нем.
Доверительное событие –
событие, которое происходит всегда, т.е. является ![]() .
.
Невозможное событие ![]() - событие, которое никогда не
происходит, т.к. не содержит ни одного элементарного события.
- событие, которое никогда не
происходит, т.к. не содержит ни одного элементарного события.
![]() : событие
: событие ![]() входит
(включено) в событие
входит
(включено) в событие ![]() ,
если наступление события
,
если наступление события ![]() влечет
за собой наступление события
влечет
за собой наступление события ![]() .
.
![]() : события
: события ![]() и
и ![]() считаются равными,
если одновременно
считаются равными,
если одновременно ![]() и
и
![]() .
.
![]() : произведение (пересечение)
двух событий
: произведение (пересечение)
двух событий ![]() и
и
![]() - событие
- событие ![]() , происходящее тогда и только тогда,
когда происходят оба события
, происходящее тогда и только тогда,
когда происходят оба события ![]() и
и ![]() ,
т.е. состоит из элементарных исходов, принадлежащих одновременно обоим событиям.
,
т.е. состоит из элементарных исходов, принадлежащих одновременно обоим событиям.
События ![]() и
и ![]() несовместны,
если
несовместны,
если ![]() .
.
![]() или
или ![]() : сумма (объединение)
событий
: сумма (объединение)
событий ![]() и
и ![]() - событие
- событие ![]() , которое происходит тогда и только
тогда, когда происходит хотя бы одно из событий
, которое происходит тогда и только
тогда, когда происходит хотя бы одно из событий ![]() и
и ![]() , т.е. состоит из элементарных
событий, принадлежащих хотя бы одному из исходных событий.
, т.е. состоит из элементарных
событий, принадлежащих хотя бы одному из исходных событий.
![]() : разность
событий
: разность
событий ![]() и
и
![]() - событие
- событие ![]() , которое происходит тогда и только
тогда, когда происходит событие
, которое происходит тогда и только
тогда, когда происходит событие ![]() и
не происходит событие
и
не происходит событие ![]() ,
т.е. состоит из элементарных событий, которые принадлежат первому и не
принадлежат второму событию.
,
т.е. состоит из элементарных событий, которые принадлежат первому и не
принадлежат второму событию.
![]() : дополнение (противоположное
событие)события
: дополнение (противоположное
событие)события ![]() -
событие
-
событие ![]() , которое
происходит тогда и только когда, когда
, которое
происходит тогда и только когда, когда ![]() не происходит.
не происходит.
![]() : симметрическая разность
двух событий
: симметрическая разность
двух событий ![]() и
и
![]() - это событие
- это событие ![]() , равное объединению событий
, равное объединению событий ![]() и
и ![]() .
.
1.
коммутативность: ![]() ,
, ![]() ;
;
2.
ассоциативность: ![]() ,
, ![]() ;
;
3.
распределительные законы: ![]() ,
, ![]() ;
;
4. поглощение:
![]() ;
(было в упражнениях в методе)
;
(было в упражнениях в методе)
5.
![]() ;
;
6.
![]() .
.
![]() -множество – любое подмножество
множества
-множество – любое подмножество
множества ![]() .
.
Алгебра событий – это
такая система ![]()
![]() -множеств, если
-множеств, если ![]() ,
, ![]() , а также
, а также ![]() , если
, если ![]() , или это класс
, или это класс ![]() -множеств, замкнутый относительно
конечного числа арифметических операций (умножение, сложение, вычитание).
-множеств, замкнутый относительно
конечного числа арифметических операций (умножение, сложение, вычитание).
![]() -алгебра – это класс
-алгебра – это класс ![]()
![]() -множеств из бесконечного множества
элементарных исходов
-множеств из бесконечного множества
элементарных исходов ![]() ,
удовлетворяющий условиям:
,
удовлетворяющий условиям: ![]() ,
,
![]() и если событий
и если событий ![]() , то и событие
, то и событие 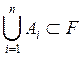 , или это класс
, или это класс ![]() -множеств, замкнутый относительно
счетного числа арифметических операций.
-множеств, замкнутый относительно
счетного числа арифметических операций.
![]() : измеримое пространство –
пара объектов
: измеримое пространство –
пара объектов ![]() и
и
![]() .
.
Вероятность события ![]() - величина
- величина 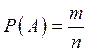 , или выраженная числом возможность
появления события
, или выраженная числом возможность
появления события ![]() .
.
1.
![]() ;
;
2.
![]() ;
;
3.
![]() ;
;
4.
![]() ;
;
5.
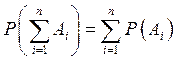 , если
, если ![]() .
.
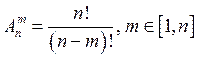 : размещения из
: размещения из ![]() элементов
по
элементов
по ![]() элементов
– соединения, состоящие из
элементов
– соединения, состоящие из ![]() элементов, взятых из данных
элементов, взятых из данных ![]() элементов и
отличающихся от друг друга или самими элементами или их порядком, или это упорядоченные
элементов и
отличающихся от друг друга или самими элементами или их порядком, или это упорядоченные
![]() -элементные подмножества
множества, состоящего из
-элементные подмножества
множества, состоящего из ![]() элементов.
элементов.
![]() : перестановки – это
размещения при
: перестановки – это
размещения при ![]() .
.
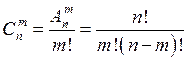 : сочетания из
: сочетания из ![]() элементов
по
элементов
по ![]() элементов
–
элементов
– ![]() -элементные соединения,
взятые из данных
-элементные соединения,
взятые из данных ![]() элементов и
отличающихся друг от друга хотя бы одним элементом, или это
элементов и
отличающихся друг от друга хотя бы одним элементом, или это ![]() -элементные неупорядоченные
подмножества множества, состоящего из
-элементные неупорядоченные
подмножества множества, состоящего из ![]() элементов.
элементов.
![]() : размещения с повторениями
из
: размещения с повторениями
из ![]() элементов
по
элементов
по ![]() элементов
– соединения по
элементов
– соединения по ![]() элементов,
причем каждый из
элементов,
причем каждый из ![]() элементов
может быть любым из
элементов
может быть любым из ![]() элементов.
элементов.
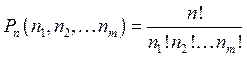 : перестановки с повторениями
из
: перестановки с повторениями
из ![]() элементов,
среди которых имеется
элементов,
среди которых имеется ![]() элементов
первого типа,
элементов
первого типа, ![]() элементов
второго, …,
элементов
второго, …, ![]() элементов
элементов
![]() -ого типа, при этом
-ого типа, при этом 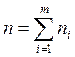 - соединения, содержащие все данные
- соединения, содержащие все данные
![]() элементов
с указанными числами повторений одинаковых элементов и отличающихся друг от
друга только порядком элементов.
элементов
с указанными числами повторений одинаковых элементов и отличающихся друг от
друга только порядком элементов.
Сочетания с повторениями
- ![]() .
.
Гипергеометрическое
распределение - 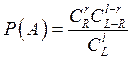 , где
, где ![]() - общее количество элементов,
- общее количество элементов, ![]() - количество выбранных элементов,
- количество выбранных элементов, ![]() - количество отличных от всех
элементов,
- количество отличных от всех
элементов, ![]() - количество
выбранных отличных элементов.
- количество
выбранных отличных элементов.
|
Выборка |
с возвращением |
без возвращения |
|
упорядоченная |
|
|
|
неупорядоченная |
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.