Принцип геометрической вероятности состоит в следующем:
1. множество
![]() рассматривается
как некоторое непрерывное ограниченное множество с бесконечным количеством
элементов;
рассматривается
как некоторое непрерывное ограниченное множество с бесконечным количеством
элементов;
2. опыт
состоит в бросании идеальной точки (без размера и веса) в это множество ![]() ;
;
3. вероятность
попадания ее в какую-то область ![]() пропорциональна
мере этой области
пропорциональна
мере этой области ![]() .
.
и утверждает, что вероятность
наступления события ![]() определяется,
как
определяется,
как 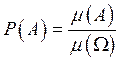 , и что выбор любой точки
из
, и что выбор любой точки
из ![]() равновозможен.
равновозможен.
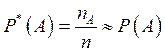 : относительная частота
события
: относительная частота
события ![]() - отношение
числа
- отношение
числа ![]() опытов,
в которых событие
опытов,
в которых событие ![]() произошло,
к числу проведенных опытов.
произошло,
к числу проведенных опытов.
Вероятность события ![]() из
из ![]() -алгебры
-алгебры ![]() называется
вещественная функция, определенная на
называется
вещественная функция, определенная на ![]() и
удовлетворяющая следующим свойствам (аксиомам):
и
удовлетворяющая следующим свойствам (аксиомам):
1.
![]() ;
;
2.
![]() ;
;
3.
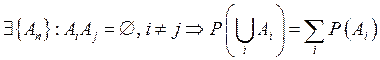 .
.
Вероятностная мера –
вероятность, заданная на ![]() -алгебре
-алгебре
![]() .
.
Вероятностное
пространство – тройка объектов ![]() ,
где
,
где ![]() - пространство
элементарных событий,
- пространство
элементарных событий, ![]() -
-
![]() -алгебра
-алгебра ![]() -множеств,
-множеств, ![]() - вероятностная мера на измеримом
пространстве
- вероятностная мера на измеримом
пространстве ![]() .
.
3’. Если события ![]() несовместны,
то
несовместны,
то 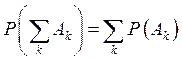 ;
;
4. Пусть
последовательно событий ![]() такова, что
такова, что 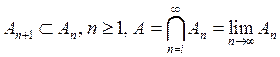 ,
тогда
,
тогда ![]() (аксиома
непрерывности).
(аксиома
непрерывности).
1.
![]() ;
;
2.
![]() ;
;
3.
![]() . Следствие:
. Следствие:
![]() ;
;
4.
![]() ;
;
5.
![]() (формула
вероятности суммы событий);
(формула
вероятности суммы событий);
6.
![]() ;
;
7.
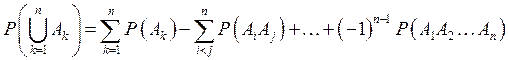 ;
;
8.
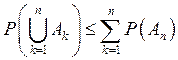 ;
;
9. Если
монотонная последовательность событий ![]() и
и
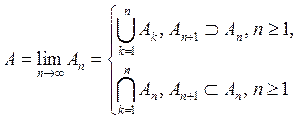 , то
, то ![]() .
.
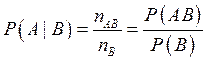 : условная вероятность –
вероятность события
: условная вероятность –
вероятность события ![]() при
условии, что в опыте произошло событие
при
условии, что в опыте произошло событие ![]() .
.
Формула
умножения вероятностей - ![]() .
.
События
![]() и
и
![]() независимы,
если
независимы,
если ![]() .
.
Свойства независимых событий:
1. ![]() или
или ![]() . Следствие: если событие
. Следствие: если событие ![]() не зависит
от события
не зависит
от события ![]() , то и событие
, то и событие ![]() не зависит от события
не зависит от события ![]() ;
;
2. Если
события ![]() и
и
![]() независимы,
то независимы события
независимы,
то независимы события ![]() и
и ![]() ,
,
![]() и
и
![]() ,
, ![]() и
и ![]() .
.
3. Если
события ![]() и
и
![]() ,
, ![]() и
и ![]() независимы
и
независимы
и ![]() , то независимы и события
, то независимы и события ![]() и
и ![]() .
.
4. Если
события ![]() независимы в
совокупности, то
независимы в
совокупности, то 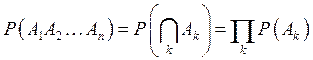 .
.
5. Пусть
![]() - независимые в
совокупности события и
- независимые в
совокупности события и 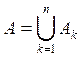 ,
то
,
то 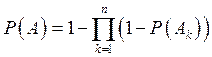 (формула вероятности
суммы независимых в совокупности событий).
(формула вероятности
суммы независимых в совокупности событий).
События
![]() независимы
в совокупности, если для
независимы
в совокупности, если для ![]() .
.
Полная
группа событий – это события ![]() такие,
что
такие,
что ![]() ;
; ![]() ;
; 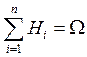 , где
, где ![]() - вероятностное пространство, а
- вероятностное пространство, а ![]() - гипотезы.
- гипотезы.
Формула
полной вероятности - 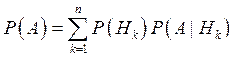 с учетом справедливости определения полной группы событий.
с учетом справедливости определения полной группы событий.
Если
![]() - априорные
вероятности гипотез, а
- априорные
вероятности гипотез, а ![]() -
апостериорные вероятности гипотез после того, как произошло событие
-
апостериорные вероятности гипотез после того, как произошло событие ![]() , то
, то 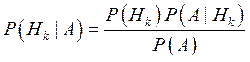 - формула Байеса.
- формула Байеса.
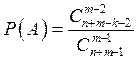 : статистика Бозе-Эйнштейна,
которой подчиняются фотоны, атомные ядра, атомы с четным число частиц, если
: статистика Бозе-Эйнштейна,
которой подчиняются фотоны, атомные ядра, атомы с четным число частиц, если ![]() - число неразличимых частиц,
- число неразличимых частиц, ![]() - количество ячеек,
- количество ячеек, ![]() - в ячейку попало
- в ячейку попало ![]() частиц (в
ячейке сколь угодно много частиц).
частиц (в
ячейке сколь угодно много частиц).
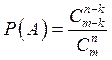 : статистика Ферми-Дирака,
которой подчиняются электроны, протоны, нейтроны, если
: статистика Ферми-Дирака,
которой подчиняются электроны, протоны, нейтроны, если ![]() частиц,
частиц, ![]() ячеек,
ячеек, ![]() - занято
- занято ![]() фиксированных
ячеек (в ячейке не более одной частицы).
фиксированных
ячеек (в ячейке не более одной частицы).
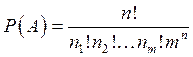 : статистика Максвелла-Больцмана,
которой подчиняется идеальный газ, если
: статистика Максвелла-Больцмана,
которой подчиняется идеальный газ, если ![]() частиц,
частиц, ![]() ячеек,
ячеек, 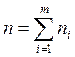 , A – в
, A – в ![]() -ую ячейку попало ровно
-ую ячейку попало ровно ![]() частиц.
частиц.
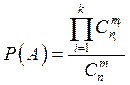 : гипергеометрическое
распределение, если
: гипергеометрическое
распределение, если 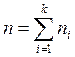 частиц
частиц
![]() -ых типов,
-ых типов, 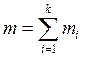 выбранных
частиц
выбранных
частиц ![]() -ого типа.
-ого типа.
Схема
Бернулли (последовательность независимых одинаковых испытаний, или биноминальная
схема испытаний) – эксперимент, удовлетворяющий условиям: у эксперимента
два исхода – появление или не появление некоторого события; эксперимент
выполняется независимо ![]() раз; вероятности обоих исходов при каждом испытании
одинаковы.
раз; вероятности обоих исходов при каждом испытании
одинаковы.
![]() : формула Бернулли – вероятность
наступления
: формула Бернулли – вероятность
наступления ![]() успехов
в серии из
успехов
в серии из ![]() независимых
испытаний, если успех в каждом отдельном испытании наступает с вероятностью
независимых
испытаний, если успех в каждом отдельном испытании наступает с вероятностью ![]() .
.
Теорема
Пуассона (распределение Пуассона). Если число испытаний ![]() в схеме
Бернулли велико, вероятность успеха
в схеме
Бернулли велико, вероятность успеха ![]() в одном испытании мала и мало также число
в одном испытании мала и мало также число ![]() , тогда
, тогда 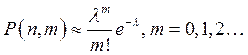
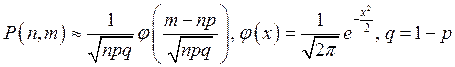 : локальная теорема
Муавра-Лапласа – если в схеме Бернулли число испытаний
: локальная теорема
Муавра-Лапласа – если в схеме Бернулли число испытаний ![]() велико, то для всех
велико, то для всех ![]() справедливо
данное приближенное равенство.
справедливо
данное приближенное равенство.
Интегральная
теорема Муавра-Лапласа. Если в схеме Бернулли число испытаний ![]() велико, то
вероятность того, что число успехов
велико, то
вероятность того, что число успехов ![]() заключено в границах от
заключено в границах от ![]() до
до ![]() , приближенно равна
, приближенно равна ![]() , где
, где
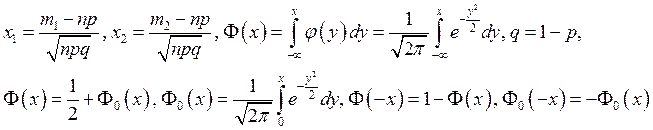
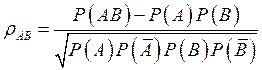 : коэффициент корреляции между
событиями – мера зависимости между событиями.
: коэффициент корреляции между
событиями – мера зависимости между событиями.
Свойства:
1.
![]() ;
;
2.
![]() ;
;
3. ![]() с точностью
до множества элементарных событий меры 0;
с точностью
до множества элементарных событий меры 0;
4. ![]() с точностью до множества
элементарных событий меры 0;
с точностью до множества
элементарных событий меры 0;
5.
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.