Построение дискретного аналога методом конечных элементов., страница 2

double x;

x = i*h;

return x;

}

double ku(int i, double *u)

{ //k(u) function :-)

return C*sqrt(fabs(u[i]));

}

void main()

{

int dim, i, m, IterationCount=0;

double *diag, *l1, *l2, *f, *x, *u, k, Now=sqrt(n), Before=0;

diag = new double [n];

l1 = new double [n-1]; //Lower diag :-)

l2 = new double [n-1]; //Upper diag :-)

f = new double [n];

x = new double [n];

u = new double [n];

for (i=0; i<n; i++) u[i] = 1.0;

while (fabs(Now-Before)>Eps &&

IterationCount < MaxIterations)

{

memset(diag, 0, n*sizeof(double));

memset(f, 0, n*sizeof(double));

memset(l1, 0, (n-1)*sizeof(double));

memset(l2, 0, (n-1)*sizeof(double));

//Build MATRIX!!! :-)

for (i=0; i<n-1; i++)

{

//Matrix B :-)

k = (ki(i)+ki(i+1))/2.0;//(2*i+1)*h;

diag[i] += k/(h);

l2[i] += -k/(h);

l1[i] = -k/(h);

diag[i+1] = k/(h);

//Matrix C :-)

diag[i] += (h/12.0)*(3.0*q(i) + q(i+1));

l2[i] += (h/12.0)*(q(i) + q(i+1));

l1[i] += (h/12.0)*(q(i) + q(i+1));

diag[i+1] += (h/12.0)*(q(i) + 3.0*q(i+1));

//Vector f :-)

f[i] += (h/6.0)*(2.0*fi(i) + fi(i+1));

f[i+1] += (h/6.0)*(fi(i) + 2.0*fi(i+1));

}

//Taking into account edge conditions :-)

f[0] -= C1;

f[n-1] += B*C2;

diag[n-1] += B;

//And we done! Now try to solve this system

for(i=1; i<n; i++)

{ //Using LU decomposition :-)

l2[i-1] /= diag[i-1];

diag[i] -= l2[i-1]*l1[i-1];

}

x[0] = f[0] / diag[0];

for(i=1; i<n; i++)

x[i] = (f[i] - l1[i-1]*x[i-1]) / diag[i];

u[n-1] = x[n-1];

for(i=n-2; i>=0; i--)

u[i] = x[i] - u[i+1]*l2[i];

Before = Now;

Now = 0;

for(i=0; i<n; i++)

Now += u[i]*u[i];

Now = sqrt(Now);  //Calc norm of  solution

IterationCount++;

}

FILE *out;

out = fopen("solution.txt", "wt");

m = (1.0/h)/(1.0/hc);

for(i=0; i<n; i++)

if (i%m == 0) fprintf(out, "%d\t%f\t%e\t%e\t%e\n",i,i*h ,u[i], ui(i),fabs(u[i]-ui(i)));

fclose(out);

}


Теперь, используя эту программу, проведем ряд вычислительных экспериментов на различных тестах:

  1. Тесты с фиксированным коэффициентом теплопроводности ()
  2. Тесты с коэффициентом теплопроводности, зависящим от  ()
  3. Тесты с коэффициентом теплопроводности, зависящим от  ()

Функции в интегралах интерполировались базисными, т. к. этот метод показал более хорошие результаты по сравнению с взятием средних значений.

Для задач, в которых  решение находилось итерационно.

Решение СЛАУ проводилось методом LU-разложения.

Результаты вычислительных экспериментов приведены ниже.

Выводы и анализ вычислительных экспериментов.

Рассматривая результаты тестов с линейной функцией решения (№3) видно, что практически точное решение получается даже при достаточно большом шаге (), в то время как дальнейшее дробление сетки приводит к увеличению размерности матрицы, и, как следствие, к увеличению числа ее обусловленности, что мешает нам получать точное решение.

При отсутствии подобных последствий (увеличение числа обусловленности матрицы, появление очень малых чисел, дающих большую погрешность) решение на более мелкой сетке получается более точным, как это видно на тестах №2, 5, 6, 7, 8. Таким образом, выбирать шаг нужно исходя из конкретной  задачи.

Линейные функции, а также полиномы небольших степеней приближаются достаточно точно, в то время как приближение осциллирующих и быстроизменяющихся функций дает существенную погрешность. Ситуацию можно улучшить, взяв в качестве базисных квадратичные функции.

Как видно из результатов, на всех тестах оценка порядка аппроксимации по правилу Рунге (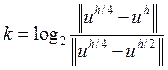) составила примерно 2, что соответствует теоретическим предположениям.

Скорее всего положительные результаты дало бы сгущение сетки на интервалах наибольшего роста функций, но здесь мы рассматривали только равномерную сетку.

При итерационном вычислении решения на точность повлияло максимальное количество итераций, которое на некоторых тестах достигалось до достижения необходимой точности, т. е. при больших вычислительных затратах можно получить более точное решение.

Скачать файл