Цель работы: Для краевой задачи, описывающей процесс стационарной одномерной теплопроводности, выписать эквивалентную вариационную постановку, построить дискретный аналог методом конечных элементов.
Содержание работы
Дано операторное уравнение ![]() ,
которое описывает процесс стационарной одномерной теплопроводности, где
,
которое описывает процесс стационарной одномерной теплопроводности, где ![]() - дифференциальный оператор, действующий в
Гильбертовом пространстве
- дифференциальный оператор, действующий в
Гильбертовом пространстве ![]() . Будем решать его
(уравнение) методом Галёркина, который основан на том, что мы находим
приближение искомой функции
. Будем решать его
(уравнение) методом Галёркина, который основан на том, что мы находим
приближение искомой функции ![]() в Гильбертовом
пространстве
в Гильбертовом
пространстве ![]() базисными функциями, и невязка
базисными функциями, и невязка ![]() в нем равна нулю тогда и только тогда, когда
она ортогональна всем векторам любой полной системы, т. е.
в нем равна нулю тогда и только тогда, когда
она ортогональна всем векторам любой полной системы, т. е. ![]() , где
, где ![]() -
пробная функция (из подпространства, где базисные функции удовлетворяют краевым
условиям). Поэтому для определения приближённого решения данного уравнения в
заданном конечномерном подпространстве пространства
-
пробная функция (из подпространства, где базисные функции удовлетворяют краевым
условиям). Поэтому для определения приближённого решения данного уравнения в
заданном конечномерном подпространстве пространства ![]() достаточно
выписать условие ортогональности невязки всем базисным векторам этого
подпространства:
достаточно
выписать условие ортогональности невязки всем базисным векторам этого
подпространства: ![]() ,
, ![]() , при
этом не требуется самосопряжённость оператора
, при
этом не требуется самосопряжённость оператора ![]() .
.
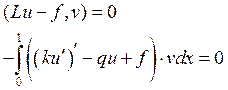
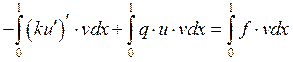
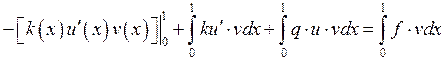
Поскольку приближённое решение ![]() принадлежит
подпространству
принадлежит
подпространству ![]() , то оно может быть представлено
в виде линейной комбинации базисных финитных функций:
, то оно может быть представлено
в виде линейной комбинации базисных финитных функций: 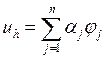 ,
где
,
где ![]() - базисные функции пространства, для
которых пробные являются подпространством.
- базисные функции пространства, для
которых пробные являются подпространством.
![]() - любая функция
- любая функция ![]() ,
, ![]()
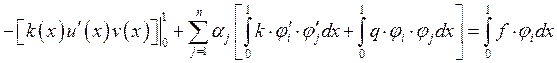
При задании 2-х и 3-х краевых условий:
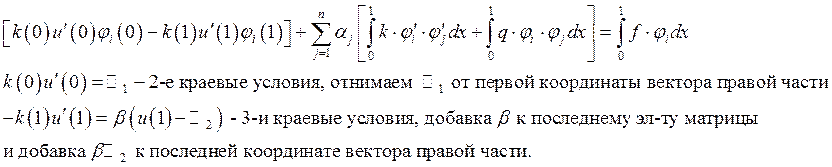
Таким образом, мы получили СЛАУ, решив которую получим коэффициенты разложения искомой функции по базисным, в качестве которых выберем финитные функции вида:
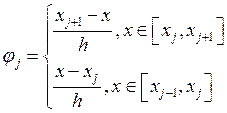 , которые равны единице только в одном узле отрезка, таким
образом, целесообразно рассматривать по отдельности каждый интервал
, которые равны единице только в одном узле отрезка, таким
образом, целесообразно рассматривать по отдельности каждый интервал ![]() , на котором функция не равна 0 – конечный
элемент, и на нём локальные матрицы массы и жёсткости, и вектор правой части.
, на котором функция не равна 0 – конечный
элемент, и на нём локальные матрицы массы и жёсткости, и вектор правой части.
Локальную матрицу А будем собирать как сумму матриц В и С, где
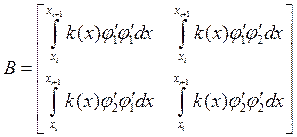 - это матрица массы, которая с
учетом интерполяции функции
- это матрица массы, которая с
учетом интерполяции функции ![]() примет вид:
примет вид:
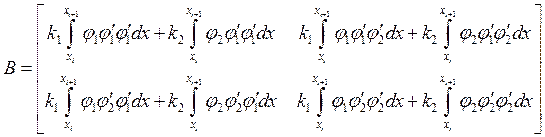 , а матрица жёсткости
, а матрица жёсткости
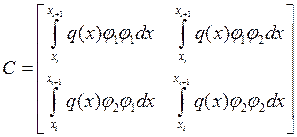 , или, с учётом интерполяции
функции
, или, с учётом интерполяции
функции ![]() :
:
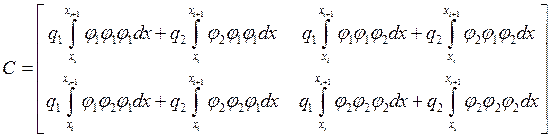
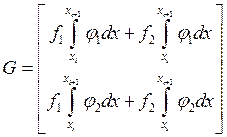 - вектор правой части.
- вектор правой части.
Посчитав эти интегралы, получаем следующие локальные матрицы массы и жёсткости, а также локальный вектор правой части:
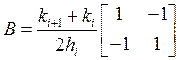 ,
, 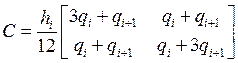 ,
, 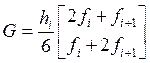 .
.
Алгоритм сборки глобальной матрицы
из локальных основан на том, каждая локальная матрица имеет в глобальной свое
местоположение, которое соответствует положению конечного элемента на отрезке.
Конечные элементы, для которых строятся локальные матрицы, «пересекаются», и
таким образом вносят свой вклад не только в элементы своей строки, но и
последующей. Т. е. последний диагональный элемент ![]() -й
матрицы складывается с первым диагональным элементом
-й
матрицы складывается с первым диагональным элементом ![]() -й
матрицы. Аналогично строится и вектор правой части. Общий вид глобальных
матрицы и вектора с учетом краевых условий, на котором все это видно приведен
ниже.
-й
матрицы. Аналогично строится и вектор правой части. Общий вид глобальных
матрицы и вектора с учетом краевых условий, на котором все это видно приведен
ниже.
Таким образом, решение краевой
задачи сводится к построению глобальной матрицы A и глобального вектора F с учетом краевых условий и последующему решению СЛАУ ![]() , где найденный вектор
, где найденный вектор ![]() содержит коэффициенты разложения искомой
функции в выбранном базисе.
содержит коэффициенты разложения искомой
функции в выбранном базисе.
Общий вид глобальной матрицы полученной СЛАУ:
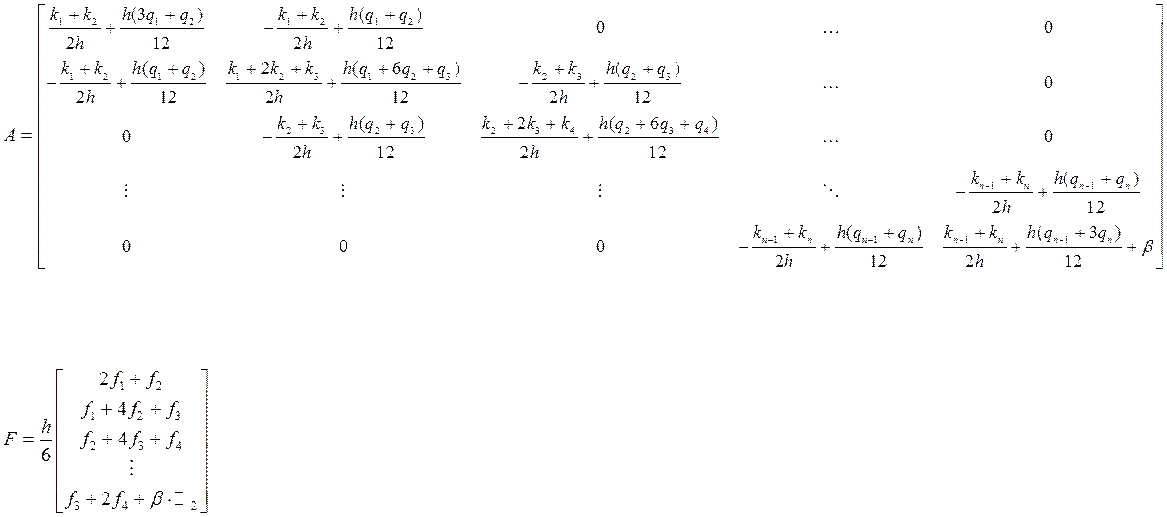
Программная реализация данного алгоритма на языке C++ приведена ниже:
#include "stdio.h"
#include "mem.h"
#include "math.h"
const int MaxIterations = 1000;
const int n = 41; //points count :-)
const double X1 = 0.0; //first point :-)
const double X2 = 1.0; //last point :-)
const double h = (X2-X1)/(n-1);
const double hc = h*4.0;
const double C = 1.0; //C from k(u) function
const double C1 = 0.0; //C1 from 2-nd edge
//conditions :-)
const double C2 = -1.0; //C2 from 3-rd edge
//conditions :-)
const double B = -1.0; //beta from 3-rd edge
//conditions :-)
const double Eps = 1e-50;
double fi(int i)
{ //f(x) function :-)
double x;
x = i*h;
return (-4.0)*x;
}
double ui(int i)
{
double x;
x = i*h;
return (x*x);
}
double q(int i)
{ //q(x) function :-)
double x;
x = i*h;
return 0.0;
}
double ki(int i)
{ //k(x) function :-)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.