Министерство образования РФ
НГТУ
Кафедра прикладной математики
Индивидуальная работа
"Моделирование псевдослучайных векторов и процессов"
Студент: Кирюшина Е.С.
Преподаватель: Цой Е.Б.
Факультет: ПМИ
Группа: ПМ-01
Вариант: 10
НОВОСИБИРСК-2004
1. Составить алгоритм моделирования случайного вектора ξ=(ξ1,…,ξn)T, распределенного в области X с плотностью f(x1,…,xn).
в) f(x)=C(x12+x22), X={xЄR2, 0≤x1≤1,0≤x2≤1}.
Найдем константу из условия нормирования функции плотности.
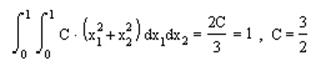
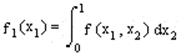
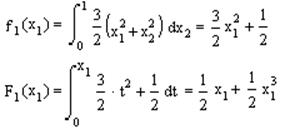
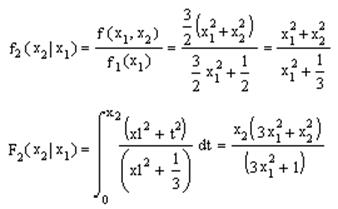
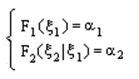
Отсюда получим:
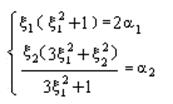
Алгоритм моделирования:
1. Моделируем α1,α2Є RAV(0,1).
2. При последовательном решении уравнений:
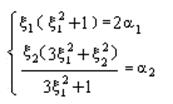
находим вектор ξ=(ξ1,ξ2)T.
2. Составить алгоритм моделирования случайного вектора ξ=(ξ1,…,ξn)T, распределенного в области X с плотностью f(x1,…,xn) по методу исключения.
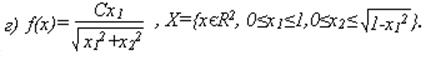
Перейдем в полярные координаты:
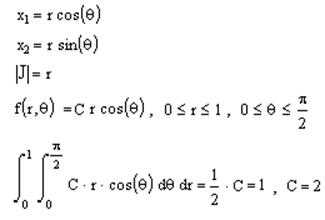
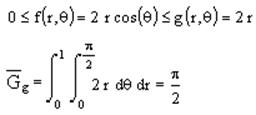
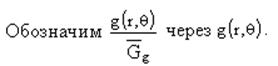
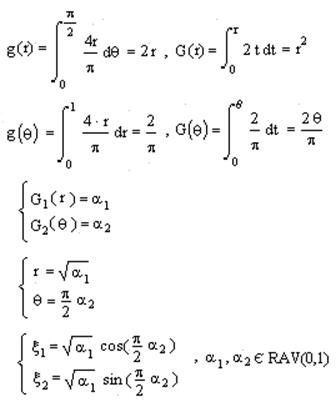
Алгоритм моделирования случайного вектора ξ=(ξ1,ξ2)T, распределенного с плотностью f(x1,x2):
1. Моделируем α1,α2,α3Є RAV(0,1).
2. Если α3≤cos(πα2/2), то
![]()
Иначе на пункт 1.
3. Найти моделирующее выражение для нормального случайного вектора ξ с дисперсионной матрицей K и математическим ожиданием m:
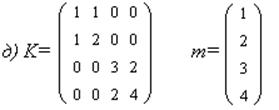
Моделирование нормального случайного вектора ξ с дисперсионной матрицей K и математическим ожиданием m можно осуществлять по формуле: ξ=Aν+m, где ν=(ν1,ν2,ν3,ν4)T , νiЄNORM(0,1).
Обычно предполагают, что A является нижней треугольной матрицей. Тогда ее элементы определяются рекуррентной формулой:
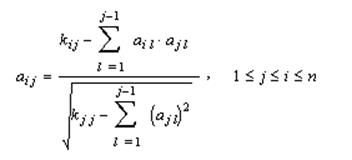
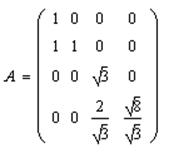
Отсюда находим вектор ξ=(ξ1,ξ2,ξ3,ξ4)T:
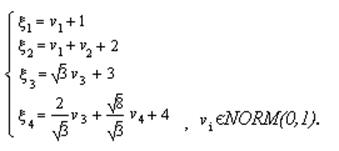
5. Найти алгоритм моделирования одномерного стационарного гауссовского марковского процесса с нулевым априорным средним и одномерной корреляционной функцией вида:
K11(t,s)=K11(t-s)=σ2e-b|t-s|, b>0.
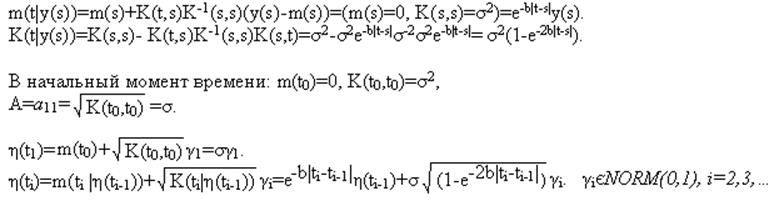
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.