III. Многомерные случайные величины
3.1.Совместная (n– мерная) функция распределения
Пусть ![]() - некоторое вероятное
пространство и
- некоторое вероятное
пространство и ![]() - случайные величины, заданные
на нем. Каждому значению
- случайные величины, заданные
на нем. Каждому значению ![]() они ставят в
соответствие вектор
они ставят в
соответствие вектор ![]() .
.
Отображение ![]() , задаваемое
совокупностью случайных величин
, задаваемое
совокупностью случайных величин ![]() , называется случайным
вектором или многомерной случайной величиной или n – мерной случайной величиной.
, называется случайным
вектором или многомерной случайной величиной или n – мерной случайной величиной.
Но если учесть, что все ![]() , измеримые
функции, случайным вектором ξ следовало бы назвать отображение
, измеримые
функции, случайным вектором ξ следовало бы назвать отображение ![]() , где В – борелевская σ – алгебра в Rn. Необходимым и достаточным условием
измеримости случайного вектора ξ является выполнение условия:
, где В – борелевская σ – алгебра в Rn. Необходимым и достаточным условием
измеримости случайного вектора ξ является выполнение условия:
![]() .
.
Справедливо утверждение [1]: n – мерная случайная величина ξ измерима тогда и только тогда,
когда все функции ![]() являются А – измеримыми
функциями.
являются А – измеримыми
функциями.
Пример 1. На
скачках, где скачут две лошади, n человек
заключают пари (между собой, группами, и т. д.). Результатами эксперимента
являются элементарные исходы ![]() - финишировала первая
лошадь,
- финишировала первая
лошадь, ![]() - финишировала вторая лошадь. Каждому элементарному исходу
может быть поставлена в соответствие многомерная случайная величина
- финишировала вторая лошадь. Каждому элементарному исходу
может быть поставлена в соответствие многомерная случайная величина ![]() , в которой
, в которой ![]() - «выигрыш» k-ого игрока в случае одного из двух исходов.
- «выигрыш» k-ого игрока в случае одного из двух исходов.
Основной характеристикой случайного вектора ξ является совместная
или n-мерная функция распределения ![]()
![]() Если положить n=2, то двумерная функция распределения есть не что иное, как
вероятность попадания точки с координатами
Если положить n=2, то двумерная функция распределения есть не что иное, как
вероятность попадания точки с координатами ![]() в заштрихованную
на рисунке область.
в заштрихованную
на рисунке область.
ξ![]() 2
2
![]()
![]() x2 (x1,x2)
x2 (x1,x2)
![]()
![]() 0 x1 ξ1
0 x1 ξ1
Далее везде будем вместо ![]() писать
писать ![]() , где упрощение
записи не вызывает недоразумений.
, где упрощение
записи не вызывает недоразумений.
Свойства совместной функции распределения случайного вектора ξ аналогичны свойствам функции распределения случайной величины, но есть и специальные, вызванные тем фактом, что ξ – вектор.
2. ![]() - функция неубывающая по каждому из своих
аргументов.
- функция неубывающая по каждому из своих
аргументов.
4. ![]()
Результат
следует из того, что событие ![]() и пересечение любого
события А с невозможным событием есть событие невозможное.
и пересечение любого
события А с невозможным событием есть событие невозможное.
5.![]() для всего множества
перестановок чисел 1,2,…,n.
для всего множества
перестановок чисел 1,2,…,n.
6.Если m<n,
то 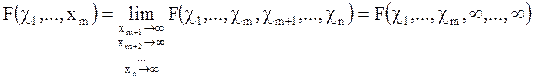 .
.
Рассмотрим
![]() , т.е.m=1. Событие
, т.е.m=1. Событие ![]() - достоверное событие,
произведение события А и достоверного события есть событие А, поэтому
- достоверное событие,
произведение события А и достоверного события есть событие А, поэтому 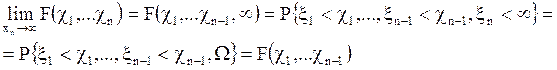
Аналогичные рассуждения можно провести для любого
1<m<n. Если m=n, то ![]() .
.
Свойства
5 и 6 называют свойством согласованности совместной функции
распределения случайного вектора ![]() .
.
Свойство
6 позволяет получить так называемые маргинальные (частные)
распределения случайных величин ![]() ,
, ![]() , если известна их совместная функция
распределения:
, если известна их совместная функция
распределения: ![]() .
.
Функция
![]() называется совместным маргинальным
распределением случайных величин
называется совместным маргинальным
распределением случайных величин ![]() .
.
7.Справедливо соотношение
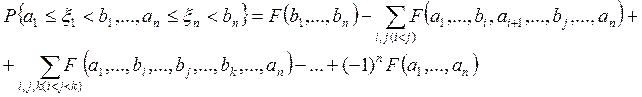
При n=2 формула принимает вид
![]()
Далее везде для простоты ограничимся рассмотрением двумерных с. величин.
3.2. Дискретные двумерные случайные величины
Двумерная случайная величина ![]() будет
дискретной, если каждая из случайных величин
будет
дискретной, если каждая из случайных величин ![]() дискретна.
Как и в одномерном случае, двумерную дискретную величину можно описать с
помощью таблицы с двумя входами, по смыслу схожей с рядом распределения
одномерной случайной величины. В верхней строке таблицы перечислены все
возможные значения случайной величины
дискретна.
Как и в одномерном случае, двумерную дискретную величину можно описать с
помощью таблицы с двумя входами, по смыслу схожей с рядом распределения
одномерной случайной величины. В верхней строке таблицы перечислены все
возможные значения случайной величины ![]() :
: ![]() ; в левом столбце – все возможные значения
случайной величины
; в левом столбце – все возможные значения
случайной величины ![]() :
: ![]() . В
клетках на пересечении строки i и столбца j записывают вероятности события
. В
клетках на пересечении строки i и столбца j записывают вероятности события ![]() . В последней строке таблицы
. В последней строке таблицы ![]() записаны числа
записаны числа 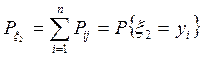 .
Следовательно, первая и последняя строки таблицы образуют ряд распределения
случайной величины
.
Следовательно, первая и последняя строки таблицы образуют ряд распределения
случайной величины ![]() . Аналогично, первый и последний
столбцы таблицы образуют ряд распределения случайной величины
. Аналогично, первый и последний
столбцы таблицы образуют ряд распределения случайной величины ![]() .
.
Таблица 2
|
|
|
|
||||
|
|
|
… |
|
|||
|
|
|
|
|
… |
|
|
|
|
|
|
… |
|
|
|
|
… |
… |
… |
… |
… |
… |
|
|
|
|
|
… |
|
|
|
|
|
|
|
… |
|
||
Таблица может быть обобщена на случай n>2.
3.3.Непрерывные n-мерные случайные величины
Если функция ![]() абсолютно
непрерывна, то случайная величина
абсолютно
непрерывна, то случайная величина ![]() называется
непрерывной. Совместную функцию распределения в этом случае можно записать в
виде n-кратного интеграла
называется
непрерывной. Совместную функцию распределения в этом случае можно записать в
виде n-кратного интеграла 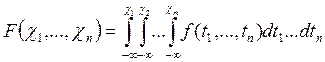 и
функция
и
функция ![]() плотность распределения n-мерной
случайной величины
плотность распределения n-мерной
случайной величины ![]() . Как и в одномерном случае будем
полагать
. Как и в одномерном случае будем
полагать 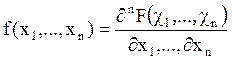 .
.
Свойства совместной плотности распределения
1. ![]()
2. 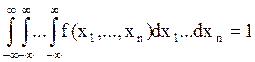
3. Если ![]() , то
, то ![]()
4. Условие согласованности для совместной плотности распределения имеет вид:
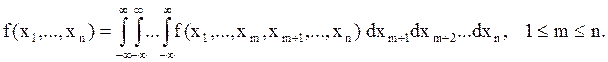
![]() -маргинальная совместная
плотность распределения случайной величины
-маргинальная совместная
плотность распределения случайной величины ![]() .
.
В частности, 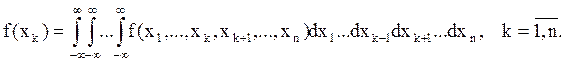 -
маргинальная плотность распределения с. величины
-
маргинальная плотность распределения с. величины ![]() ,
, ![]() .
.
В заключении рассмотрим наиболее часто встречающиеся на практике многомерное нормальное распределение (гауссово распределение).
Говорят, что с. вектор ![]() ,
компонентами которого являются непрерывные с. величины
,
компонентами которого являются непрерывные с. величины ![]() ,
,
![]() распределен по нормальному закону, если
совместная плотность распределения вектора
распределен по нормальному закону, если
совместная плотность распределения вектора ![]() определяется
формулой
определяется
формулой
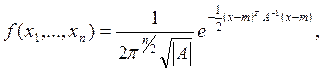 (3.1)
(3.1)
где ![]() ,
,
![]() -вектор математического ожидания с.
величины
-вектор математического ожидания с.
величины ![]() или вектор средних , положительно
определенная матрица А носит
или вектор средних , положительно
определенная матрица А носит
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.