





Новосибирский Государственный Технический Университет
Кафедра прикладной математики
по курсу: «Численные методы»
Преподаватель: Рояк М. Э., Рояк С.Е.
Задание
МКЭ для двумерной краевой задачи для эллиптического уравнения в цилиндрической (r, z) системе координат. Базисные функции бикубические (лагранжевы), прямоугольные конечные элементы. Краевые условия первого рода. Матрицу СЛАУ генерировать в плотном формате. Решать полученную СЛАУ методом LU-разложения.
Краевая задача для эллиптического уравнения
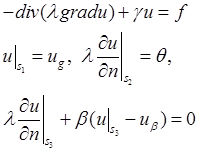
Уравнение задано в области ![]() с границей
с границей ![]() .
.
1.Вариационная постановка
Решение краевой задачи эквивалентно минимизации функционала
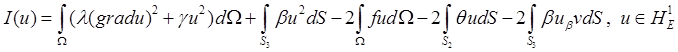
Функционал можно записать в виде
![]() , где
, где
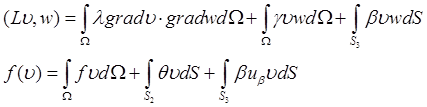
Тогда минимизация
функционала на ![]() эквивалентна решению уравнения Галёркина
эквивалентна решению уравнения Галёркина
![]() .
.
Чтобы построить
численное решение, перейдём от бесконечномерных пространств ![]() к конечномерным
к конечномерным ![]() .
Тогда уравнение Галёркина примет вид
.
Тогда уравнение Галёркина примет вид
![]()
![]() являются подпространствами Vh
, если задано краевое условие первого рода, и совпадают с Vh
, если оно не задано. Когда мы задаём краевые условия первого рода, мы
фиксируем веса части базисных функций в разложениях функций из
являются подпространствами Vh
, если задано краевое условие первого рода, и совпадают с Vh
, если оно не задано. Когда мы задаём краевые условия первого рода, мы
фиксируем веса части базисных функций в разложениях функций из ![]() .Таким образом, размерность
.Таким образом, размерность ![]() меньше размерности Vh на
число этих базисных функций с зафиксированными весами. Обозначим через N0
– множество индексов
меньше размерности Vh на
число этих базисных функций с зафиксированными весами. Обозначим через N0
– множество индексов ![]() таких, что базисные функции
таких, что базисные функции ![]() Vh являются базисными и
для
Vh являются базисными и
для ![]() .
.
Представим в виде
линейной комбинации базисных функций функции ![]() и
и ![]()
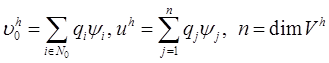 . Подставив в уравнение
, получим строку
СЛАУ для qj
. Подставив в уравнение
, получим строку
СЛАУ для qj
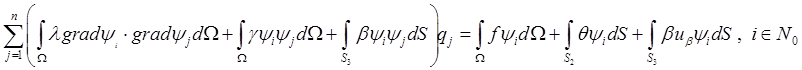 .
.
Недостающие n-N0 уравнения получим из главного краевого условия.
2.Решение задачи на прямоугольных элементах с бикубическими базисными функциями
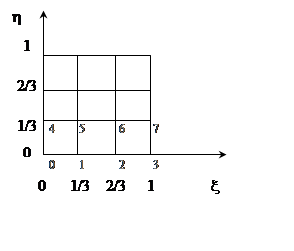 Чтобы реализовать МКЭ, в качестве базисных
функций возьмем финитные функции. Разобьём область
Чтобы реализовать МКЭ, в качестве базисных
функций возьмем финитные функции. Разобьём область ![]() на
прямоугольные конечные элементы
на
прямоугольные конечные элементы ![]() . Сделаем замену
. Сделаем замену 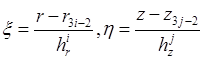 . В качестве базисных функций возьмем
бикубические лагранжевы функции. Это означает, что они кубические по обеим
переменным и строятся только по значениям функции в узлах. Для построения таких
функций на конечном элементе требуется их значение в 4 узлах по r и по z.
. В качестве базисных функций возьмем
бикубические лагранжевы функции. Это означает, что они кубические по обеим
переменным и строятся только по значениям функции в узлах. Для построения таких
функций на конечном элементе требуется их значение в 4 узлах по r и по z.
На каждом конечном
элементе определим локальные базисные функции так, чтобы каждая из них была
равна 1 в одном узле и нулю во всех остальных. Бикубические базисные функции
определяются как произведение соответствующих линейных кубических функций по r
и z: ![]() .
.
Занумеруем узлы, двигаясь по области слева направо снизу вверх. Такая нумерация будет определять вид глобальной матрицы и в значительной степени – реализацию метода.
Причем ![]() будем составлять в соответствии с
локальным порядком нумерации узлов (см. рис.), т.е., двигаясь по узлам, по r
перебираем функции
будем составлять в соответствии с
локальным порядком нумерации узлов (см. рис.), т.е., двигаясь по узлам, по r
перебираем функции ![]() , а по z -
, а по z - ![]() .
.
Параметры задачи ![]() заменим
на конечном элементе их средними значениями
заменим
на конечном элементе их средними значениями ![]() , а
функцию f - своим кубическим интерполянтом.
, а
функцию f - своим кубическим интерполянтом.
Получим выражения для локальных матриц. Для простоты рассмотрим один элемент, остальные будут вычисляться аналогично.
Для матрицы массы
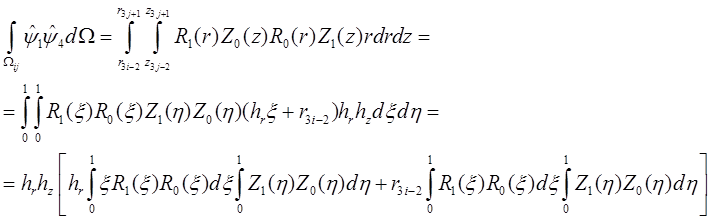
Для матрицы жёсткости
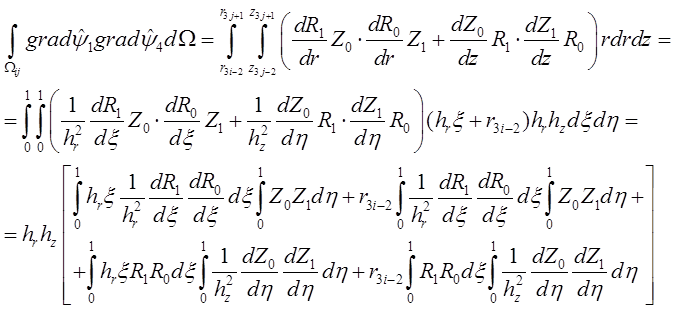
Таким образом, двойные интегралы для
вычисления элементов матриц распадаются на обычные, причём, учитывая, что 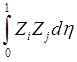 =
=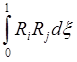 ,
, 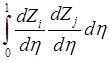 =
=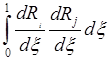 , локальную матрицу
16x16 будем формировать из 4 матриц 4x4.
, локальную матрицу
16x16 будем формировать из 4 матриц 4x4.
Локальный вектор получим, умножив матрицу массы
на вектор, компонентами которого являются значения f в узлах конечного элемента
в порядке, соответствующем локальной нумерации узлов, т.к.![]() мы интерполируем:
мы интерполируем:
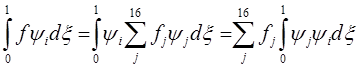
3.Сборка глобальной матрицы и вектора правой части СЛАУ
 Рассмотрим структуру локальной матрицы.
Элементы матрицы имеют вид
Рассмотрим структуру локальной матрицы.
Элементы матрицы имеют вид 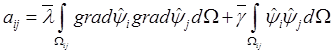 . Очевидно, что если
разбить матрицу на 16 блоков 4x4, то в первом блоке будут элементы с
произведениями функций
. Очевидно, что если
разбить матрицу на 16 блоков 4x4, то в первом блоке будут элементы с
произведениями функций ![]() , которые соответствуют
узлам
, которые соответствуют
узлам ![]() в глобальной нумерации. Эти узлы идут друг
за другом, значит в глобальную матрицу первый блок пойдёт целым, без разбиения
на части. 5 и 2 блоки также пойдут в глобальную матрицу целиком, так как узлы 4,5,6,7
и 0,1,2,3 идут друг за другом и в локальной и в глобальной матрицах.
в глобальной нумерации. Эти узлы идут друг
за другом, значит в глобальную матрицу первый блок пойдёт целым, без разбиения
на части. 5 и 2 блоки также пойдут в глобальную матрицу целиком, так как узлы 4,5,6,7
и 0,1,2,3 идут друг за другом и в локальной и в глобальной матрицах.
В случае прямоугольной области расстояние от 3 узла до 4 в глобальной сетке равно числу узлов по оси r (nr), то 5 блок в глобальной матрице, будет отстоять на nr элементов от 1 блока.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.