МКЭ для двумерной краевой задачи для эллиптического уравнения в цилиндрической (r, z) системе координат., страница 2

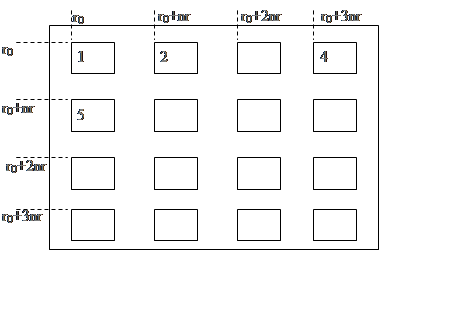
Вклад в глобальную матрицу от одного конечного элемента (r₀ – номер узла левого нижнего угла КЭ) 

Аналогично локальный вектор правой части разобьём на 4 части, которые пойдут в соответствующие компоненты глобального вектора. Вклады от различных конечных элементов будут пересекаться в тех элементах матрицы, которые соответствуют граничным узлам конечных элементов. Поэтому сначала заполним глобальные матрицу и вектор нулями, а потом будем добавлять блоки локальных матрицы и вектора к соответствующим элементам.

4.Учёт краевых условий первого рода

На элементы главной диагонали тех строк, которые соответствуют попавшим на границу узлам сетки, поставим большое число (10³⁰), а в правую часть - , умноженное на это большое число. При этом матрица останется симметричной, и в граничных узлах мы будем получать заданное значение без погрешности.

5. Формат входных данных

В каждом конечном элементе задаются координаты и номера только 4х находящихся на левом ребре прямоугольника узлов.

Файл point : <количество узлов в сетке> <количество задаваемых узлов>

<номер узла> <r координата> <z координата>

…

<номер узла> <r координата> <z координата>

Файл element : <количество конечных элементов>

<номер нижн. лев. узла> <номер верхн. лев. узла> <шаг по r> <шаг по z> <номер в каталоге>

…

<номер нижн. лев. узла> <номер верхн. лев. узла> <шаг по r> <шаг по z> <номер в каталоге>

Файл bound :

<номер краевого узла> <номер в каталоге ребер>

…

<номер краевого узла> <номер в каталоге ребер>

6.Тестирование

1) Тесты на правильность работы программы.

1.  Сборка локальных матрицы и вектора

Один конечный элемент, . Погрешность результата 2.81e-16.

Так как при формировании локального вектора мы используем матрицу массы, то тестирование на ситуации  не требуется.

2.  Сборка глобальных матрицы и вектора

Область:

Погрешность результата: 5.29e-15.

 

Область:

Погрешность: 5.06e-15.

Четыре конечных элемента. Погрешность результата: 1.53e-14.

2)Пусть , тогда 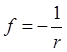 будет интерполироваться кубическими функциями с погрешностью. Выбрав сетку по r: 1,4,7; по z: 0,3 , получим погрешность 0.004923. Возьмём сетку по r: 1, 2.5, 4, получим погрешность 0.000894. Таким образом, несмотря на то, что решение – линейная функция, которая точно аппроксимируется кубическими функциями, погрешность интерполяции f существенно понижает точность решения.

 

3) Тест на непрямоугольную область. . Область:

Погрешность: 6.503е-12

 

4)Тест на дробление сетки.

         1. Погрешность: 3.495е-12. Область:

2. Погрешность: 3.347е-11. Область:

В данном случае дробление сетки только ухудшило решение. Вероятно, это связано с тем, что функция  оказалась лучше представима бикубическими функциями одного КЭ на отрезке [4,7], нежели бикубическими функциями 3х КЭ.

5) Определим порядок аппроксимации метода.

. Рассмотрим решение на:

1. одном конечном элементе: по z – 1,7, по r – 1,4;

2. двух: по z –1,4,7, по r – 1,4;

3. восьми: по z – 1, 2.5, 4, 5.5, 7, по r – 1, 2.5, 4. 

	1 КЭ	2 КЭ	8 КЭ	Аналит. решение
(2,3)	20.187021100001	19.501775743259	20.0591673720072	20.085536923187
(3,3)	20.745454040809	19.575375732551	20.06293968055732
(2,5)	119.97895690781	146.06814226399	148.2497666219908	148.41315910257
(3,5)	122.70152640984	146.43712771655	148.2719228988182
	0.0173204363124	0.0034582006114	0.000450518514660
	38.3410706660502214	8.1567565964451	1.644078645394197

Если оценивать порядок аппроксимации по правилу Рунге 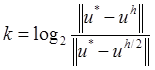, то в данном случае .