Методы моделирования произвольно распределенных непрерывных псевдослучайных величин

Новосибирский  государственный  технический  университет

Кафедра прикладной математики

Лабораторная работа №2-3

«Методы моделирования

произвольно распределенных непрерывных

псевдослучайных величин»

          Факультет:          ПМИ

          Группа:                ПМ-82

Студенты:            Андреев  Д.А.

                                         Белавин Р.В

                              Пахомов А.А.

Преподаватели:  Тишковская С. В.

                                                  Тимофеев В. С.

                                            Новосибирск

2001

Выполнение лабораторной работы №2

Моделирование и статический анализ равномерно распределенных и дискретных псевдослучайных величин

Цель работы:

Изучение программных методов имитации ранвомерно распределнных псевдослучайных величин на отрезке [0;1];  методов моделирования дискретных величин; экспериментальное исследование качества псевдослучайных последовательностей.

I. Условие задачи.

Разработать алгоритм моделирования дискретной псевдослучайной величины:

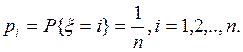
II. Содержание работы.

Общий метод моделирования дискретной случайной величины основан на соотношении:

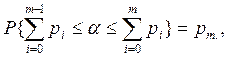 где

Таким образом качество выборки дискретной случайной величины зависит не только от параметров дискретного распределения, но и от качества выборки равномерного распределения на отрезке [0,1].

Качество выборки дискретной случайной величины можно оценить с помощью критерия согласия . Для этого используется статистика:

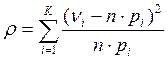, где k – количество интервалов группирования.

n_i – частота с которой встречается фиксированный элемент выборки,

p_i – теоретическая вероятность фиксированного элемента,

n – объем выборки.

Если наша гипотеза справедлива, то при достаточно большом n эта величина должна хорошо починяться закону распределения c²(k-1,1-e) – квантиль распределения c² с (k-1) степенями свободы, e – зафиксированное достаточно большое значение вероятности (доверительная вероятность), (1-e) – уровень значимости.

Пусть  - ошибка первого рода, тогда, если <c²(k-1,1-e),тогда гипотеза принимается.

1. Пусть есть линейная конгруэнтная схема: ,

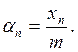
1)Если a=4.98, c=2, x₀=0, m=5, объем выборки N=200, n=10 и k=9, , то 2.975.

2)Если a=4.8, c=2, x₀=0, m=5, объем выборки N=200, n=10 и k=9, , то 10.675.

Так как =9.52, то в случае (1) выборка соответствует требуемому распределению, а в случае (2) нет. Так как качество выборки в случае (2) равномерного распределения на отрезке [0,1] хуже чем в первом случае, то и качество выборки дискретного распределения в случае (2) заметно ниже.

2. Пусть a=4.98, c=2, x₀=0, m=5, объем выборки N=500, =0.1, k=n.

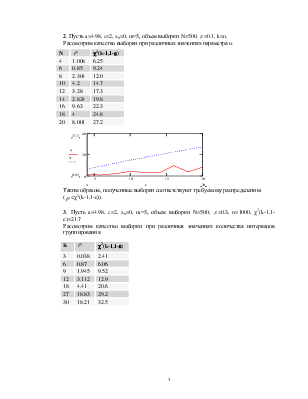
Рассмотрим качество выборки при различных значениях параметра n.

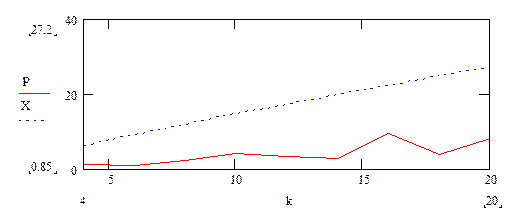
Таким образом, полученные выборки соответствуют требуемому распределению

(<c²(k-1,1-e)).

3. Пусть a=4.98, c=2, x₀=0, m=5, объем выборки N=500, =0.3, n=1000, c²(k-1,1-e)=21.7

Рассмотрим качество выборки при различных значениях количества интервалов группирования.

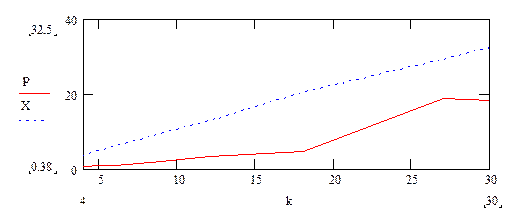
Таким образом, полученные выборки соответствуют требуемому распределению

(<c²(k-1,1-e)).

4. Пусть a=4.98, c=2, x₀=0, m=5, объем выборки N=500, n=1000, k=27. В этом случае значение статистики=18.83. При различных значениях  имеем:

a)  Если =0.05, то гипотеза о том, что выборка согласована с требуемым распределением, принимается, так как  c²(k-1,1-e)=38.9.

b)  Если =0.1, то гипотеза о том, что выборка согласована с требуемым распределением, принимается, так как  c²(k-1,1-e)=35.6.

Программа:

#include <conio.h>

#include <fstream.h>

#include <stdlib.h>

#include <stdio.h>

#include <math.h>

const dim=100;

const m=1000;    // parameter mod

int k,N,n;     // parameters gipergeometrition model

int nnn;

/***** METHOD 1: X=(a*x0+c) mod m  *****/