Методы моделирования произвольно распределенных непрерывных псевдослучайных величин, страница 3

Для  задана плотность распределения , где .

Случай 1. - монотонно возрастает. Найдем функцию распределения для .

  

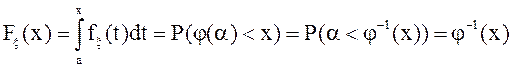
Действительно,

.

   .

Случай 2. - монотонно убывает. Найдем функцию распределения для .

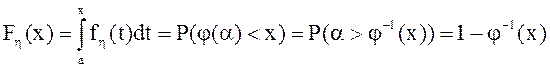
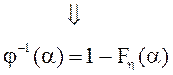
Действительно,

.

   .

Отметим, что случайные величины  и  одинаково распределены. Иногда замена  на  упрощает формулу расчета.

Если функция  не является монотонной, то для плотности распределения случайной величины  не существует универсального выражения.

Т.о. задача о выборе формулы усложняется, если допустить немонотонность . Практически можно ограничиться функциями , которые монотонны и дифференцируемы в каждом из интервалов счетного разбиения отрезка [0;1]. Строить моделирующие формулы можно на основе следующего утверждения:

Утверждение.

Пусть , .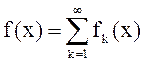

Обозначим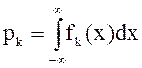

,  ,

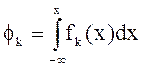
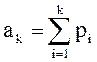Случайная величина , при  имеет плотность распределения .

2. метод суперпозиции

                               

3. Метод исключения

Пусть   Пусть

Алгоритм  для   с 

1.  2. если  то  goto 1 else

Смоделировав  по заданному методу «псевдослучайные числа» проверяем гипотезу об том, что полученная последовательность непрерывно  распределена. Проверку производим  по критерию согласия c².

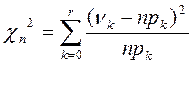,  r- количество разбиений области допустимых значений

n- Объем выборки

H₀:  c²(n) <  c² ( r-1 , 1-b )

Гипотеза о том, что «псевдослучайные числа» непрерывно распределены, принимается  с ошибкой первого рода 1-b

Исследование задачи №1

f(x)=l exp( -lx ) Î Exp(l)

xÎ(0;¥)

Число индивидуальных наблюдений n = 200

Экспоненциальное (1е-7, 0.000000)

Критерий согласия	Вероятность
Отношения правдоподобия( 2) Отношения правдоподобия( 4) Хи-квадрат( 2)             Хи-квадрат( 4)             Колмогорова                Смирнова                    Омега(малое)-квадрат       Омега(большое)-квадрат	0.8548669191 0.9889181496 0.8525911188 0.9885582506 0.9772871137 0.9890075922 0.9747343659 0.8487566113

Экспоненциальное (1.000000, 0.000000)

Критерий согласия	Вероятность
Отношения правдоподобия( 2) Отношения правдоподобия( 4) Хи-квадрат( 2)             Хи-квадрат( 4)             Колмогорова                Смирнова                   Омега(малое)-квадрат       Омега(большое)-квадрат	0.8548656496 0.9889179505 0.8525898356 0.9885580459 0.9772870541 0.9890078902 0.9747346044 0.8487588763

Экспоненциальное (1000.000000, 0.000000)

Критерий согласия	Вероятность
Отношения правдоподобия( 2) Отношения правдоподобия( 4) Хи-квадрат( 2)             Хи-квадрат( 4)             Колмогорова                Смирнова                   Омега(малое)-квадрат       Омега(большое)-квадрат	0.8551684701 0.9889653825 0.8528647792 0.9886018487 0.9774920940 0.9893733263 0.9746754169 0.8485860229

Проверка производилась с помощью пакета  из  Лабораторной работы №1

По всем критериям согласия гипотеза принимается с вероятностью близкой к единице  при любом параметре l  Экспоненциального распределения.

Исследование задачи №2

f(x)=C x ( 1+x )²

xÎ(0;1)

_n- число индивидуальных наблюдений

c² – статистика хи-квадрат ракспределения

e - ошибка первого рода