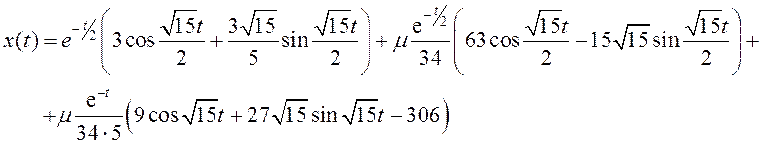
Построим график зависимости координаты от времени и
фазовый портрет колебаний осциллятора (траектория движения исходит из точки ![]() ):
):
3. Построить аналитическое решение, соответствующее субгармоническому
резонансу для случая, когда ![]() .
.
Уравнение перепишем в следующем виде:
![]()
Воспользуемся методом последовательных приближений,
обозначив ![]() , и ограничившись учетом членов разложения
по малому параметру 1-го порядка:
, и ограничившись учетом членов разложения
по малому параметру 1-го порядка:
![]()
С учетом обозначений примет вид:
![]()
Подставим соотношение в :
![]()
Уравнение нулевого приближения:
![]()
Решение имеет вид:
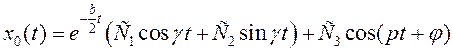 , где
, где
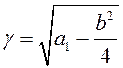 ,
,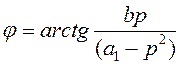 ,
,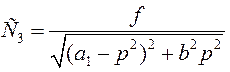
С учетом начальных условий и значений коэффициентов, константы равны:

Тогда
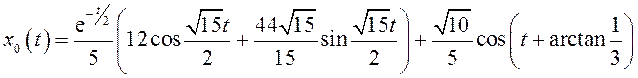
Уравнение первого приближения:
![]()
Подставив в решение и значения коэффициентов, получим:
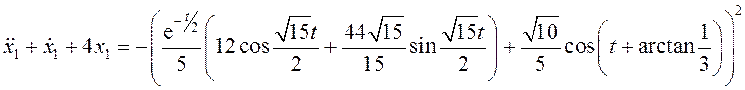
Решая это уравнения найдем решение ![]() :
:
![]()
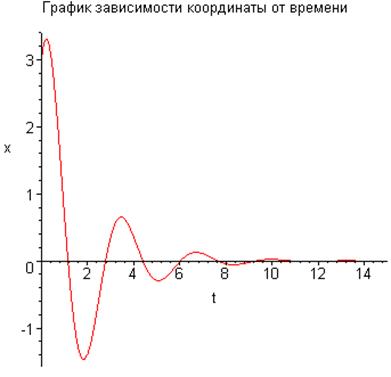
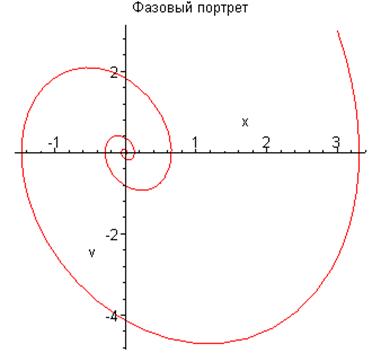
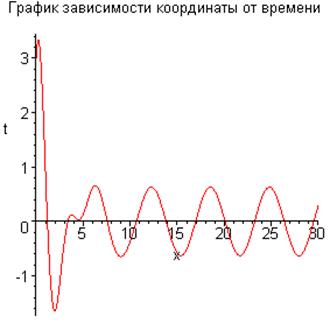
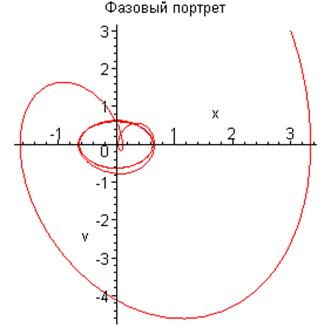
Построим график зависимости координаты от времени и
фазовый портрет колебаний осциллятора (траектория движения исходит из точки ![]() ):
):
4. Построить численное решение
В качестве численного метода решения уравнения был использован метод Рунге-Кутта.
Уравнение будет иметь вид:
![]()
Взяты начальные условия и шаг ![]() .
.
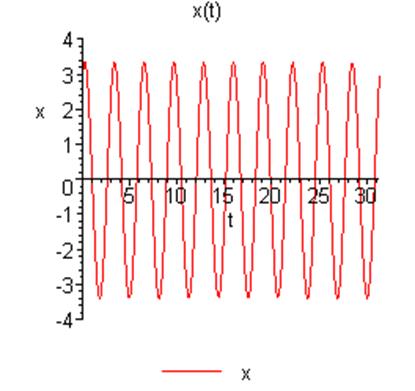
График зависимости решения от времени:
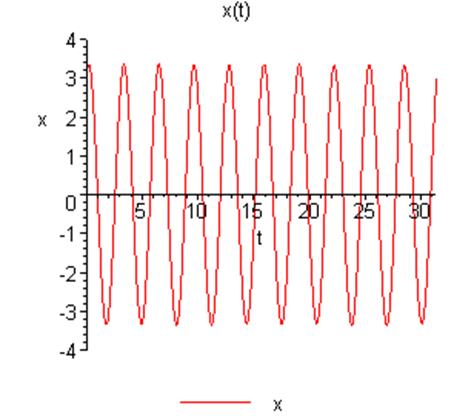
Фазовый портрет:
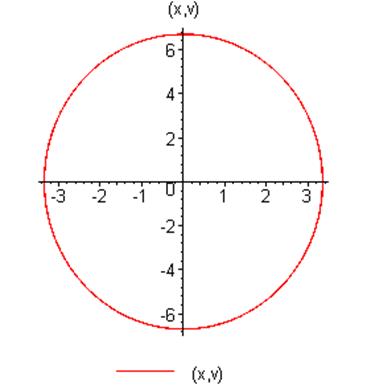
Уравнение будет иметь вид:
![]()
При данных начальных условиях и шаге![]() график
зависимости решения от времени и фазовый портрет будут выглядеть следующим образом:
график
зависимости решения от времени и фазовый портрет будут выглядеть следующим образом:
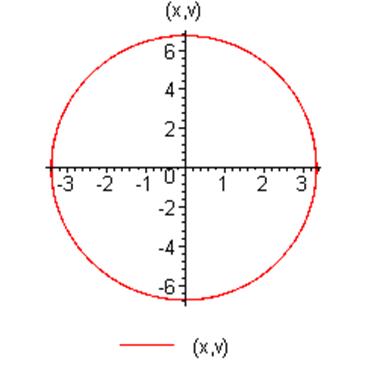
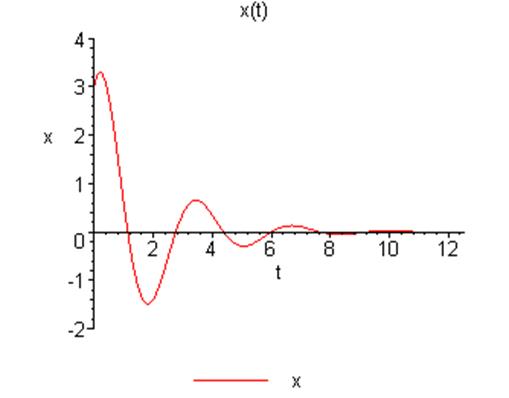
Уравнение будет иметь вид:
![]()
Колебания осциллятора представляют собой синусоиду,
затухающую с течением времени по экспоненте. При данных начальных условиях и шаге![]() график
зависимости решения от времени и фазовый портрет будут выглядеть следующим
образом:
график
зависимости решения от времени и фазовый портрет будут выглядеть следующим
образом:
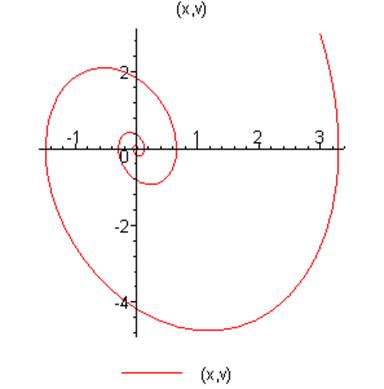
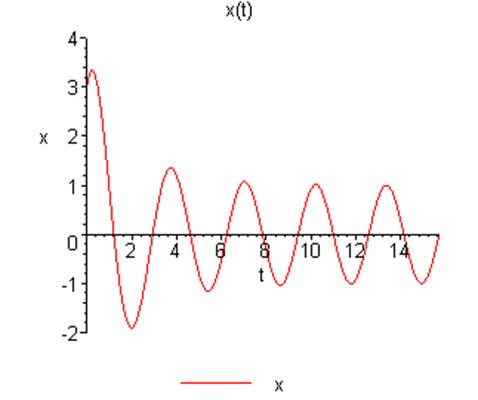
Уравнение будет иметь вид:
![]()
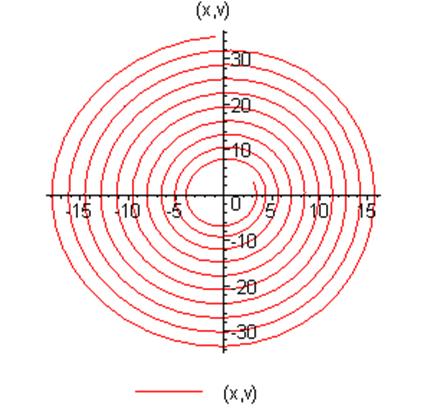
Фазовая траектория движения осциллятора сворачивается в эллипс за счет затухания экспоненциальной компоненты решения, обусловленной трением, и осциллятор продолжает свое колебание под действием вынуждающей силы.
Взяты начальные условия и шаг ![]() . График зависимости
решения от времени и фазовый портрет приведены ниже:
. График зависимости
решения от времени и фазовый портрет приведены ниже:
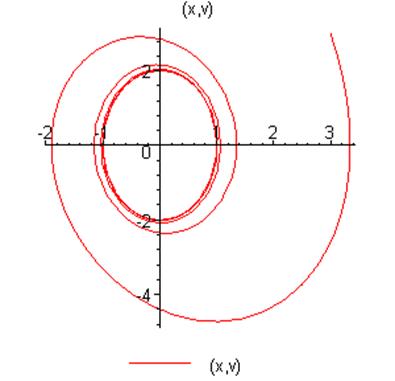
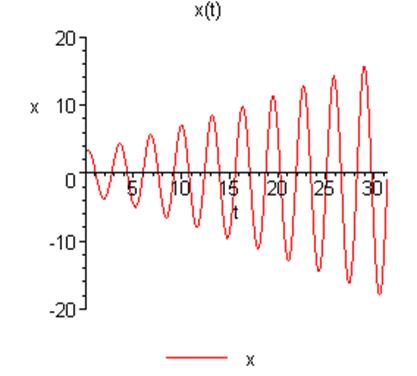
Уравнение будет иметь вид:
![]()
Фазовая траектория движения
осциллятора раскручивается вокруг начала координат: за счет накачки энергии в
систему и при отсутствии трения энергия системы увеличивается, и,
соответственно, увеличивается скорость и амплитуда колебаний. Взяты начальные
условия и шаг ![]() . График зависимости
решения от времени и фазовый портрет приведены ниже:
. График зависимости
решения от времени и фазовый портрет приведены ниже:
Уравнение будет иметь вид:
![]()
Явление субгармонического резонанса возможно при
частоте вынуждающей силы 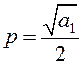 . Тогда уравнение можно
переписать в виде:
. Тогда уравнение можно
переписать в виде:
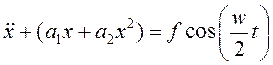
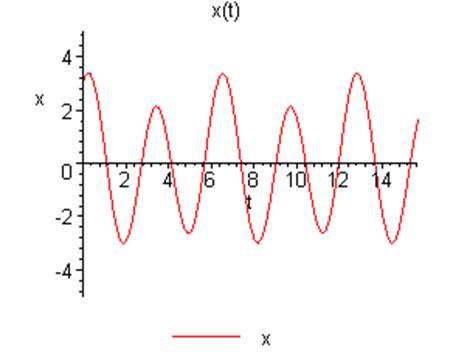
Взяты
начальные условия и шаг ![]() . График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
. График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
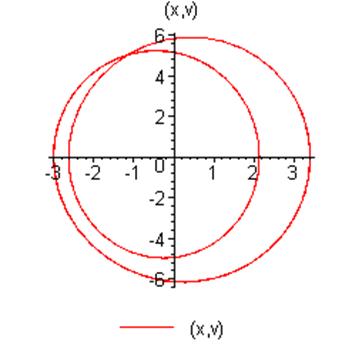
При
![]() уравнение будет иметь вид:
уравнение будет иметь вид:
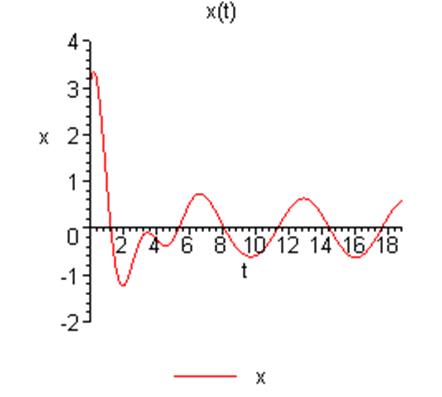
Взяты
начальные условия и шаг ![]() . График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
. График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
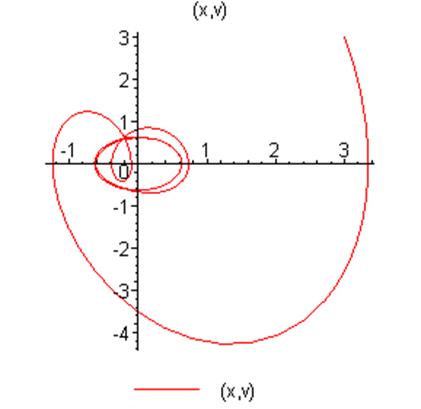
Явление параметрического резонанса возможно при
частоте вынуждающей силы ![]() ,
, ![]() Было взято значение
Было взято значение ![]() .
.
Уравнение будет иметь вид:
![]()
Взяты
начальные условия и шаг ![]() . График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
. График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
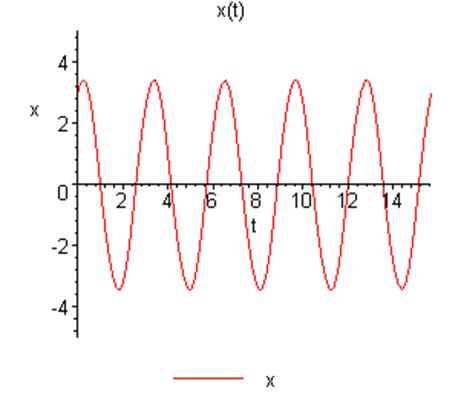
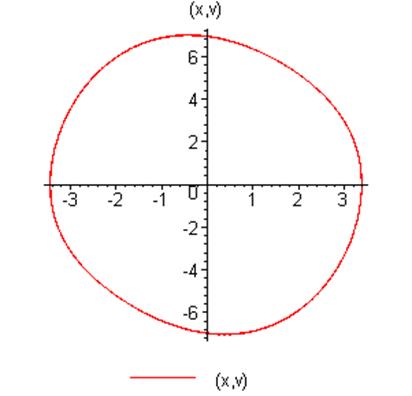
Уравнение будет иметь вид:
![]()
Взяты
начальные условия и шаг ![]() . График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
. График зависимости
решения от времени и фазовый портрет выглядят следующим образом:
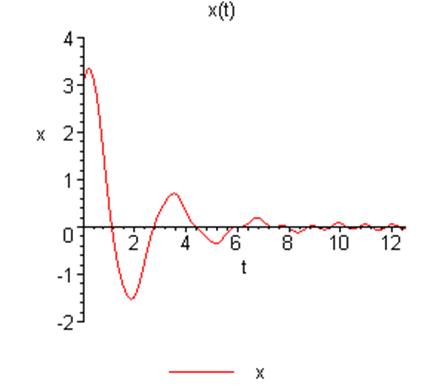
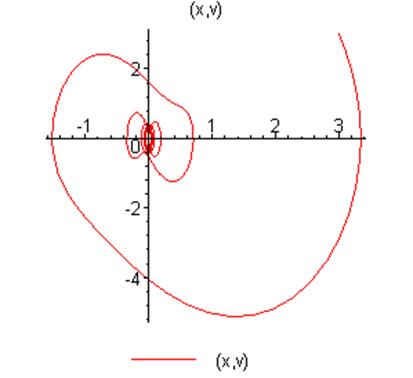
Уравнение будет иметь вид:
![]()
По
определению, решение ![]() устойчиво по Ляпунову:
устойчиво по Ляпунову:
если ![]() такое,
что при
такое,
что при ![]() выполняется
выполняется ![]()
![]() .
.
Для определения устойчивости численного решения рассмотрим следующую величину:
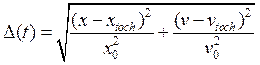
Точным решением будем считать численное решение, просчитанное тем же методом с шагом меньшим на порядок (это можно, поскольку используется метод Рунге-Кутта с 4 порядком аппроксимации).
Построены графики зависимости
величины ![]() .
.
Шаг вычисления составляет ![]() .
.
Для численного решения шаг вычисления ![]() .
.
Начальные условия: ![]() .
.
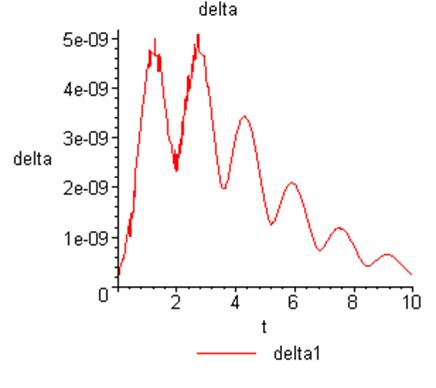
Начальные условия: ![]() .
.
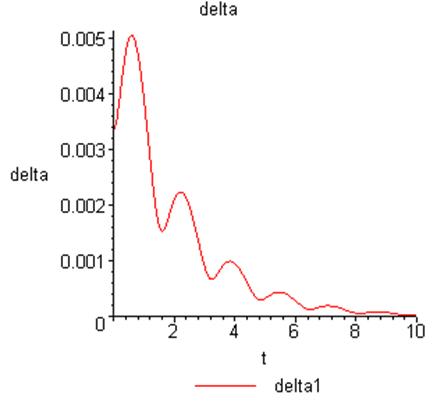
Начальные условия: ![]() .
.
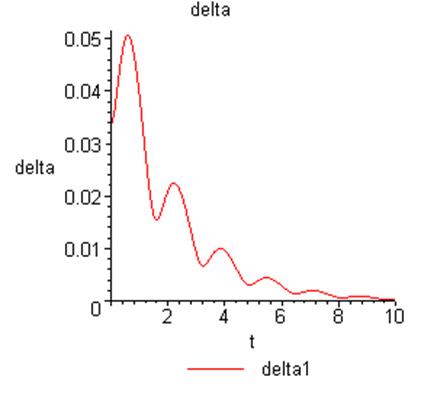
Для всех вариаций шага ![]() .
.
Вывод: решение, полученное численным путем, устойчиво относительно малых вариаций начальных данных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.