Методы моделирования природных явлений и технологических процессов

Министерство образования и науки РФ

Новосибирский государственный технический университет

Лабораторная работа №1

дисциплина:

Методы моделирования

природных явлений и технологических процессов

Факультет: ПМИ

Группа: ПМ-23

Студенты: Ефимова А.А.

                    Чусовкова А.В.

Преподаватель: Рудяк В.Я.

Вариант: 1.6

Новосибирск

2006

Постановка задачи

Дана нелинейная колебательная система, описываемая уравнением

.                                             

Значения коэффициентов и начальных данных:

                               

Выполнение задания

1.   Исследовать численно и аналитически линейный резонанс в системе

1.1  

Примем , , , тогда уравнение перепишем в следующем виде:

                                                       

Уравнение будем решать методом вариации постоянных.

Общее решение уравнения представим в виде:

,                                               где  - неизвестные функции,  - частные решения однородного уравнения, соответствующего уравнению . Они равны:, , т.е.

                                               

По искомому методу производные функции  должны иметь такой же вид, какой они имели бы при постоянных , откуда следует:

                                       

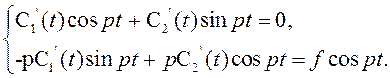
Выразим :

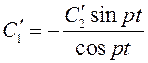
Подставим во второе уравнение системы :

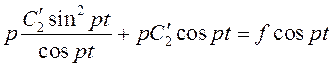
Тогда получим :

                                       

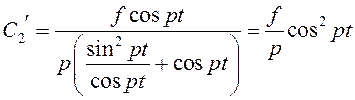
Подставим в уравнение для  и получим соответствующее выражение:

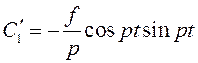
Тогда решение системы для  и  имеет вид :

                                                  

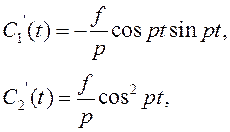
Проинтегрируем соотношения :

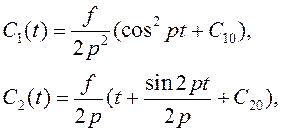
Подставим  и  в , и с учетом начальных условий вычислим свободные коэффициенты.

Подставим в уравнение для x, учитывая, что :

                                                        

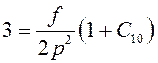
Отсюда получим:

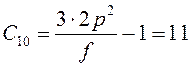
Теперь определим , учитывая, что :

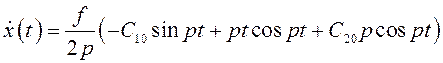
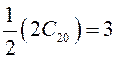
Получили, что , .

В результате приведения подобных в уравнении для x получим решение уравнения :

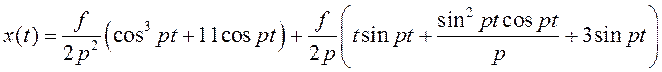
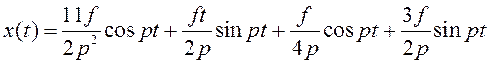
Окончательно получим следующее соотношение для x:

                                                                                                                                                                 

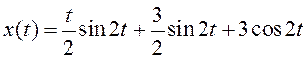
Тогда .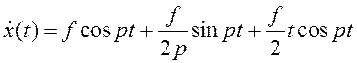

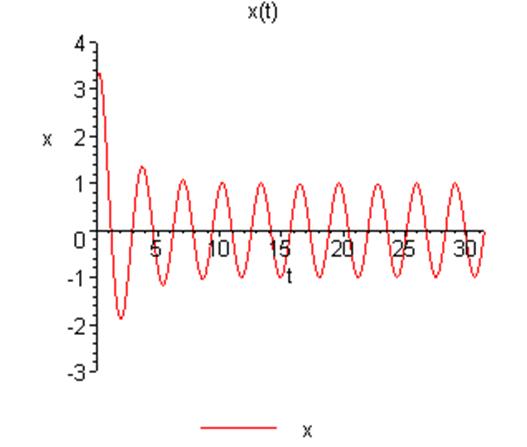
Ниже приведен график решения:

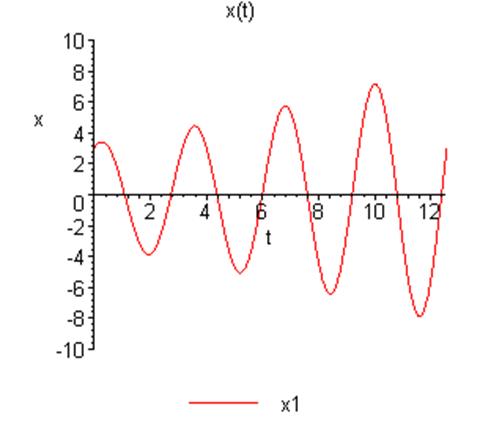
Фазовый портрет будет выглядеть следующим образом:

1.2  

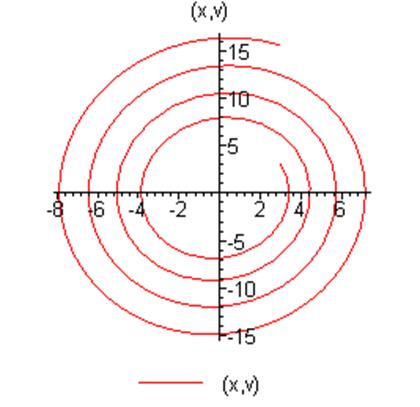
Примем , , тогда уравнение перепишем в виде :

                                                    

Представим общее решение уравнения в виде:

,                                                      

где - решение однородного уравнения, соответствующего ,  - частное решение .

Вычислим , представив его в виде:

                                                     

Найдем показатели ,, решая характеристическое уравнение:

                                                     

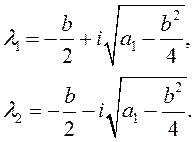
Подставив значения показателей в , получим:

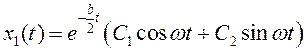,                                            где

                                                          

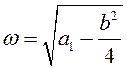
Для поиска  воспользуемся  методом комплексных амплитуд.

По определению комплексная амплитуда , где  - модуль комплексной амплитуды,  - аргумент (фаза) колебания. Запишем уравнение    с комплексной вынуждающей силой  :

                                                       

Решение будем искать в виде . В силу линейности решение  содержит вещественную часть, которая относится к уравнению . Тогда

 

или

                                                     

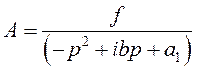
Модуль  комплексной амплитуды   и аргумент (фаза)   будет выглядеть следующим образом:

                                                 

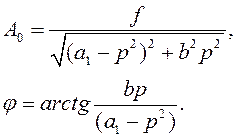
Следовательно, частное решение имеет вид:

                                  подставляя соотношения в , получим:

                           

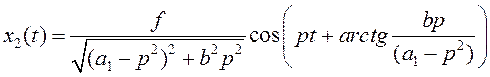
Суммируя и , получаем общее решение:

                                   

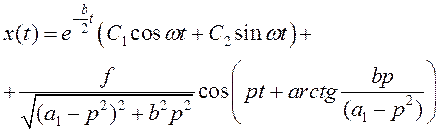
Найдем  и , учитывая, что :

                                               

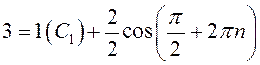
Получим, что .

Из условия  определим .

                                    

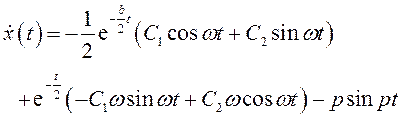
Тогда, учитывая начальное значение производной, получим:

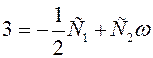
Получили, что .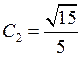

Можно записать окончательное решение:

                               

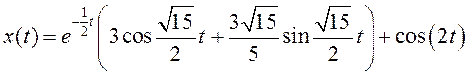
Представим графики зависимости решения от времени:

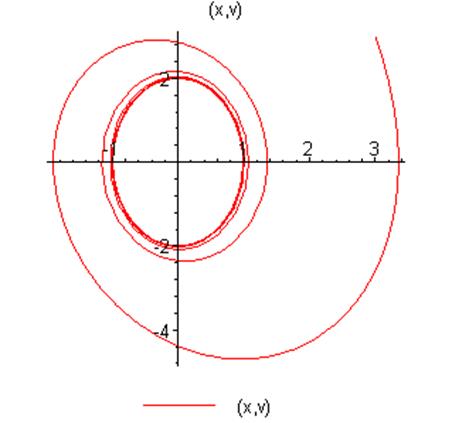
Ниже приведен фазовый портрет для этого случая: (траектория движения исходит из точки ):

2.  Построить аналитическое решение , считая, что , . Ограничиться учетом членов порядка . Положить .

Уравнение перепишем в следующем виде:

                                                    

Воспользуемся методом последовательных приближений, обозначив , и ограничившись  учетом членов разложения по малому параметру 1-го порядка:

                                                            

С учетом обозначений примет вид:

                                                    

Подставим соотношение   в :

                    

Уравнение нулевого приближения:

                                                       

Решение имеет вид:

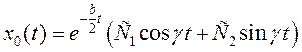,                                            где

                                                           

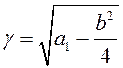
Производная решения имеет вид:

                                  

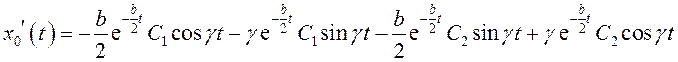
Вычислим коэффициенты  и  с учетом начальных условий:

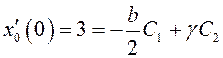
Из этого уравнения получим:

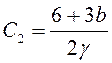
Итак, коэффициенты уравнения найдены, подставим решение в уравнение первого приближения:

                                 

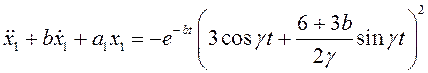
Подставим значения параметров:

                               

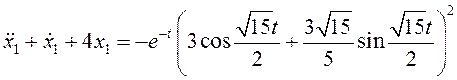
Решим неоднородное уравнение с нулевыми начальными условниями:

                                                                                                             

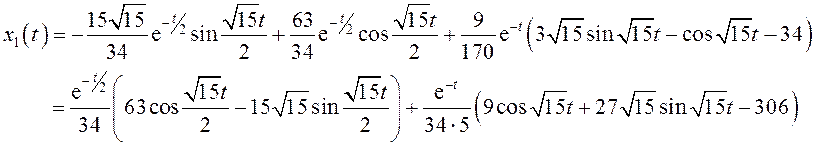
Тогда решение в виде будет: