Метод исключения

Министерство образования и науки

Новосибирский Государственный Технический Университет

Курсовая работа

по дисциплине:

«Методы планирования и анализа в экономических и социологических исследованиях»

Факультет:         ПМИ

Группа:              ПМ-04

Преподаватель: Еланцева  И.Л.

Полетаева И.А.

Студент:            Сайтгалин А.А.

Вариант:               17

Новосибирск 2004

Постановка задачи:

Выбор наилучшей регрессионной модели методом исключения. 

Методы расчетов:

Метод исключения корректирует структуру модели в следующем порядке: Заранее оценивается самая полная модель. После этого подсчитывают значения частных F - критериев для каждого регрессора при условии, что именно он исключается из модели. В результате из модели исключается регрессор, имеющий наименьшее значение частного F - критерия:

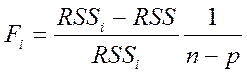, где

 - остаточная сумма квадратов для модели без i-го регрессора;

 - остаточная сумма квадратов для модели со структурой, включающей i-й регрессор;

n - число экспериментов;

p - полное число регрессоров;

В приведенном алгоритме не используются какие-либо правила останова, выполнение процедур доводится до модели, содержащей один регрессор. Выбор наилучшей модели производиться по статистике Малоуса:

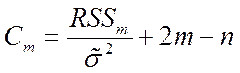, где

 - остаточная сумма квадратов, рассчитанная по модели с m регрессорами;

- подходящая оценка для ;

В  качестве оценки неизвестной дисперсии была выбрана .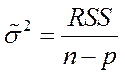

Для всех построенных моделей вычисляется статистика Малоуса и в качестве наилучшей модели выбирается модель с наименьшим значением .

Описание программы:

Программа считывает данные из файла x.txt, следующего формата: первая строка файла должна содержать число факторов и число наблюдений (через пробел). Последующие строки должны содержать значения факторов с последним  значением в строке - значение отклика.

На стандартный вывод программа выводит наилучшую регрессионную модель.

Тесты:

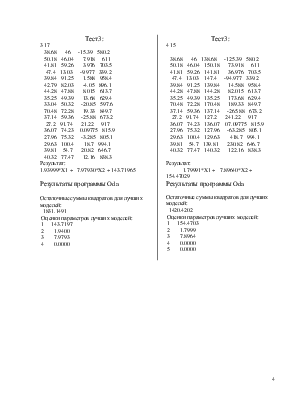
Тест1:

3 21

38.68      46      15.39   580.2

50.18   46.04      7.918     611

41.81   59.26      3.976   703.5

45.13   42.05      11.32     565

47.4   13.03      9.977   339.2

39.84   91.25      1.588   958.4

42.79   82.03      -4.05   896.1

41.62   69.72      10.87   779.9

44.28   47.88      8.015   613.7

35.25   49.39     -13.68   629.4

33.04   50.32      20.85   597.6

70.48   72.28      19.33   849.7

37.14   59.36      25.88   673.2

27.2   91.74      21.22     917

47.59   40.82      17.34   554.3

36.07   74.23    0.09775   815.9

27.96   75.32      3.285   805.1

29.63   100.4       18.7   994.1

39.81    54.7      20.82   646.7

40.32   77.47      12.16   838.3

42.65   96.38     0.7733    1006

Результат:

1.99966*X1 +   8.00240*X2 +  -1.00511*X3 + 149.95933

Результаты программы Oda

Остаточные суммы квадратов для лучших моделей:

0.8501

Оценки параметров лучших моделей:

1     149.9593

2       1.9997

3       8.0024

4      -1.0051

Тест2:

3 21

38.68      46   15.39   684.1

50.18   46.04   7.918   698.1

41.81   59.26   3.976   834.5

45.13   42.05   11.32   873.8

47.4   13.03   9.977   766.6

39.84   91.25   1.588   744.4

42.79   82.03   -4.05   802.7

41.62   69.72   10.87   696.2

44.28   47.88   8.015   760.4

35.25   49.39  -13.68   543.1

33.04   50.32   20.85   779.7

70.48   72.28   19.33    1001

37.14   59.36   25.88   595.3

27.2   91.74   21.22   864.3

47.59   40.82   17.34   769.2

36.07   74.23 0.09775   615.1

27.96   75.32   3.285   891.5

29.63   100.4    18.7   788.9

39.81    54.7   20.82   623.6

40.32   77.47   12.16     504

42.65   96.38  0.7733   620.5

Результат:

736.04762

Результаты программы Oda

Остаточные суммы квадратов для лучших моделей:

308554.4724

Оценки параметров лучших моделей:

1     736.0476

2       0.0000

3       0.0000

4       0.0000