



Неопределённый интегралсовокупность первообразных ф-ии.
Св-ва
f интегрируема, ∫f(x)dx=F(x)+C
1. ∫df(x)=f(x) d∫f(x)dx=f(x)dx d(∫f(x)dx)/dx=f(x)
2. ∫(![]() akfk(x))dx=
akfk(x))dx=![]() ak∫fk(x)dx
ak∫fk(x)dx
3. ∫f(ax+b)dx=![]() F(ax+b)+C
F(ax+b)+C
Замена переменных
Пусть f(x)
определена на промежутке Δx, g(t)определена на Δt, g(Δt)![]() Δx, g(t)
дифференцируема на Δt, f(x) интегрируема на Δx. Тогда ∫f(g(t))·
Δx, g(t)
дифференцируема на Δt, f(x) интегрируема на Δx. Тогда ∫f(g(t))·![]() ’(t)dt=F(g(t))+C.
’(t)dt=F(g(t))+C.
g(Δt)![]() Δx, f определена на Δx
Δx, f определена на Δx![]() f(g(t)) определена на Δt.
f(g(t)) определена на Δt.
F-первообразная
для f![]() F определена и диф-ма на Δх, F(g(t))
определена и диф-ма на Δt.
F определена и диф-ма на Δх, F(g(t))
определена и диф-ма на Δt.
(F(g(t)))’=F’(g(t))·g’(t)=f(g(t))·g’(t).
Интегрирование по частям
Пусть u(x) и v(x)
опр-ны и диф-мы на Δ, ![]() ∫u dv.
Тогда
∫u dv.
Тогда ![]() ∫vdu=u·v-∫u dv.
∫vdu=u·v-∫u dv.
u·v опр-но и диф-мо на Δ
d(uv)=udv+vdu
∫d(uv)= ∫ v du+∫u dv
по
св-вам неопр. ∫ ∫d(uv)=uv![]() ∫ v du=u·v-∫u dv
∫ v du=u·v-∫u dv
Интегрирование дробно-рациональных ф-ий
Любой полином n-ной
степени имеет ровно n корней с учётом их кратности. При этом если все
коэф-ты ![]() R, то комплексные корни будут
образовывать сопряжённые пары.
R, то комплексные корни будут
образовывать сопряжённые пары.
f(x)=![]()
![]() *Pt(x)=c
*Pt(x)=c![]()
![]() ·...·
·...·![]()
![]()
![]() ·...·
·...·![]()
Если знаменатель ф-ии f
представлен в виде * , то f(x)=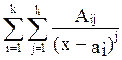 +
+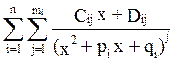 .
.
Каждому из множителей в разложении знаменателя соответствует столько слагаемых в сумме, какова степень этого множителя, степени знаменателей в этих слагаемых постепенно возрастают. Коэф-ты A, C, D находятся с помощью метода неопределённых коэф-тов: 1) сложить все дроби в сумме, 2) приравнять числитель получившегося выр-я к числителю исходной ф-ии.
В силу линейности ∫ ∫f(x)dx=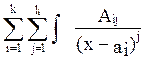 dx+
dx+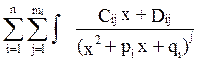 dx.
dx.
Т. о. интегрирование любой дробно-рациональной ф-ии может быть сведено к выч-ю интегралов
1) 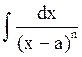
при n=1 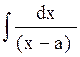 =ln|x-a|+C, при n>1
=ln|x-a|+C, при n>1 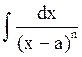 =
=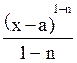 +C
+C
2) ![]()
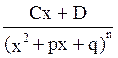 dx={t=x+p/2}=C
dx={t=x+p/2}=C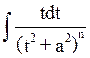 +
+
+(D-Cp/2)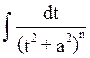
где a2=q-p2/4, при n=1 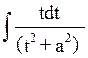 =1/2ln(t2+a2)+C, при n≠0
=1/2ln(t2+a2)+C, при n≠0 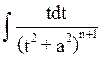 =-
=-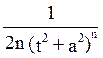 +C,
+C,
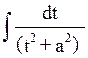 =
=![]() arctg
arctg![]() +C,
+C,
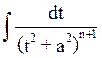 =
=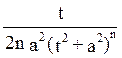 +
+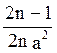
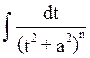 +C
+C
В рез-тате интегрирования любой дробно-рациональной ф-ии получается выр-е, в к-е входят 3 типа ф-ий: 1) дробно-рациональные ф-ии - рациональная часть, 2) ln и 3)arctg – трансцендентная часть.
Метод Остроградского
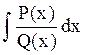 =
=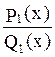 +
+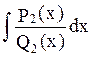
Q(x)=c![]()
![]() ·...·
·...·![]()
![]()
![]() ·...·
·...·![]()
Q1=gcd(Q,Q’)=c![]()
![]() ·...·
·...·![]()
![]()
![]() ·...·
·...·![]()
Q2=Q/Q1
deg P1=deg Q1-1
deg P2=deg Q2-1
P1 и P2 находятся методом неопределённых коэф-тов из продифференцированной ф-лы Остроградского.
Интегрирование иррац. ф-ий
Для нахождения ∫ов, содержащих множители вида R(x) применяются след. гиперболич. и тригонометрич. подстановки:
R(x)=![]()
x=a sint dx=a cost dt R(x)=a cost ч
x=a cost dx=-a sint dt R(x)=a sint ч
x=a
tht dx=![]() R(x)=
R(x)=![]() з
з
R(x)=![]()
x=a
tgt dx=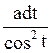 R(x)=
R(x)=![]() з
з
x=a sht dx=a cht dt R(x)=a cht ч
R(x)=![]()
x=![]() dx=
dx=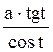 dt R(x)=
dt R(x)=![]() з
з
x=a
ctht dx=-![]() R(x)=
R(x)=![]() з
з
x=a cht dx=a sht dt R(x)=a sht ч
{ подстановка используется «ч» - если R(x) – в числителе, «з»-в знаменателе }
Интегрирование рациональных тригонометрич. и гиперболич. ф-ий
∫R(sinx,cosx)dx подстановка z=tg(x/2)
тогда sinx=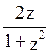
![]() , cosx=
, cosx=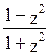 , dx=
, dx=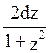
∫R(shx,chx)dx подстановка z=th(x/2)
тогда shx=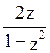
![]() , chx=
, chx=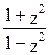 , dx=
, dx=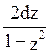
3 ситуации, когда выч-я можно упростить:
1)R(-x,y)=-R(x,y)
подстановка z=cosx или z=chx
2)R(x,-y)=-R(x,y)
подстановка z=sinx или z=shx
3)R(-x,-y)=R(x,y)
подстановка z=tgx или z=thx
Подстановки Эйлера (для ∫ов вида ∫R(x,![]() )dx)
)dx)
1) a>0
![]() =t-
=t-![]()
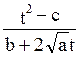
x=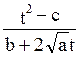
dx=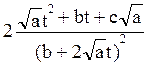
2) c>0
![]() =
=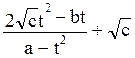
x=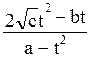
dx=2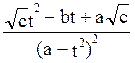 dt
dt
3) ax2+bx+c=a(x-x1)(x-x2)
t=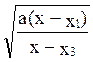
![]() =t·|
=t·|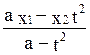 -x2|
-x2|
{выражение под ![]() д. б. неотрицательным
д. б. неотрицательным ![]() знак при раскрытии | | однозначен}
знак при раскрытии | | однозначен}
x=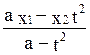
dx=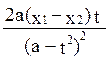 dt
dt
∫ от дифференциального бинома
т. Эйлера-Чебышева
∫ от дифференциального бинома xm(a+bxn)p м. б. сведён к ∫ от дробно-рациональной ф-ии только в 3х случаях:
1) p![]() Z
Z
Если p>0 , то (a+bxn)p – бином Ньютона.
Если
p<0 , то xm(a+bxn)p=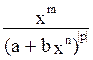 . Тогда если m,n
. Тогда если m,n![]() Z, то выр-е уже дробно-рациональное, иначе его можно
свести к дробно-рациональной ф-ии заменой x=zq, где q – наименьший общий знаменатель дробей
Z, то выр-е уже дробно-рациональное, иначе его можно
свести к дробно-рациональной ф-ии заменой x=zq, где q – наименьший общий знаменатель дробей
m и n.
2) 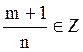
Тогда p=r/s , где r![]() Z, s
Z, s![]() N, замена (a+bxn)r/s=zr,
∫(a+bxn)r/sdx=
N, замена (a+bxn)r/s=zr,
∫(a+bxn)r/sdx=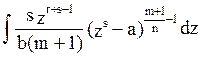
3) p+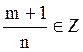
Тогда p=r/s , где r![]() Z, s
Z, s![]() N, замена zs=ax-n+b,
∫(a+bxn)r/sdx=
N, замена zs=ax-n+b,
∫(a+bxn)r/sdx=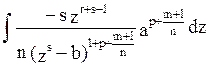
Определённый интеграл
Разбиение отрезка [a,b] Λ={a=x0<x1<...<xn=b}.
Подотрезок разбиения Δk=[xk,xk+1].
|Δk|=xk+1-xk
Мелкость разбиения |Λ|=minΔk.
Выборка Ξ={ξk ![]() Δk | k=0,...,n-1}.
Δk | k=0,...,n-1}.
mk=![]() f(x), Mk=
f(x), Mk=![]() f(x).
f(x).
Интегральная сумма Дарбу S(f,Ξ,Λ)=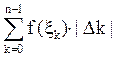 , верхняя
, верхняя ![]() (f,Λ)=
(f,Λ)=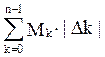 , нижняя S(f,Λ)=
, нижняя S(f,Λ)=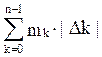 .
.
Ф-я f(x)
интегрируема по Риману на [a,b] (f![]() R[a,b]),
если у интегральных сумм S(f,Ξ,Λ) при |Λ|→0 вне зависимости от Ξ
R[a,b]),
если у интегральных сумм S(f,Ξ,Λ) при |Λ|→0 вне зависимости от Ξ ![]() предел (т. е.
предел (т. е. ![]() ε>0
ε>0 ![]() δ
δ ![]() Ξ
Ξ ![]() Λ |Λ|<δ
Λ |Λ|<δ![]() |S(f,Ξ,Λ)-I|<ε).
Значение этого предела I=
|S(f,Ξ,Λ)-I|<ε).
Значение этого предела I=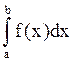 - ∫
Римана от f на [a,b].
- ∫
Римана от f на [a,b].
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.