Ограниченная на отрезке ф-я f
интегр-ма по Риману ![]()
![]() (
(![]() (f,Λ)-S(f,Λ))=0
(т. е.
(f,Λ)-S(f,Λ))=0
(т. е. ![]() ε>0
ε>0 ![]() δ
δ ![]() Λ |Λ|<δ
Λ |Λ|<δ![]()
(![]() (f,Λ)-S(f,Λ))<ε).
(f,Λ)-S(f,Λ))<ε).
![]() Ф-я
f интегр-ма по Риману
Ф-я
f интегр-ма по Риману
![]()
![]() ε>0
ε>0 ![]() δ
δ ![]() Ξ
Ξ ![]() Λ |Λ|<δ
Λ |Λ|<δ![]() |S(f,Ξ,Λ)-I|<ε/2.
|S(f,Ξ,Λ)-I|<ε/2.
I-ε/2<S(f,Ξ,Λ)<I+ε/2.
I-ε/2<S(f,Λ)![]()
![]() (f,Λ)<I+ε/2
(f,Λ)<I+ε/2 ![]() (
(![]() (f,Λ)-S(f,Λ))<ε.
(f,Λ)-S(f,Λ))<ε.
![]() Ф-я
ограничена
Ф-я
ограничена ![]() все интегр. суммы
все интегр. суммы ![]()
![]()
определены I*=supS(f,Λ), I*=inf![]() (f,Λ).
(f,Λ).
I*![]() I*,
I*, ![]() (f,Λ)
(f,Λ)![]() I*
I*![]() I*
I*![]()
![]() (f,Λ)
(f,Λ)
![]() (
(![]() (f,Λ)-S(f,Λ))=0
(f,Λ)-S(f,Λ))=0 ![]() I*=I*=I
I*=I*=I
![]() (f,Λ)
(f,Λ)![]() I
I![]()
![]() (f,Λ)
(f,Λ) ![]()
0![]() I-
I-![]() (f,Λ)
(f,Λ)![]()
![]() (f,Λ)-
(f,Λ)-![]() (f,Λ)
(f,Λ)
0![]()
![]() (f,Λ)-I
(f,Λ)-I![]()
![]() (f,Λ)-
(f,Λ)-![]() (f,Λ)
(f,Λ)
![]() (f,Λ)-
(f,Λ)-![]() (f,Λ)→0
(f,Λ)→0 ![]()
![]() (I-S(f,Λ))=
(I-S(f,Λ))=![]() (
(![]() (f,Λ)-I)=0
(f,Λ)-I)=0 ![]()
![]() S(f,Λ)=
S(f,Λ)=![]()
![]() (f,Λ)=I
(f,Λ)=I
![]() (f,Λ)
(f,Λ)![]() S(f,Ξ,Λ)
S(f,Ξ,Λ)![]()
![]() (f,Λ)
(f,Λ)
![]() S(f,Ξ,Λ)=I
S(f,Ξ,Λ)=I
Признаки интегрируемости
1) f непрерывна на
[a,b] ![]() f
f![]() R[a,b].
R[a,b].
[a,b] – компакт. По т. Больцано-Вейерштрассе f равномерно непрерывна на нём.
Произв.
ε>0. Разделим [a,b] так, чтобы на ![]()
подотрезке Δk w(f)=![]() f(x)-
f(x)-![]() f(x)
f(x)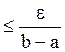 .
.
![]() (f,Λ)-
(f,Λ)-![]() (f,Λ)=
(f,Λ)=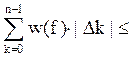
![]()
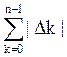 =ε
=ε
2) f монотонна на [a,b] ![]() f
f![]() R[a,b].
R[a,b].
Пусть f возрастает.
![]() (f,Λ)-
(f,Λ)-![]() (f,Λ)=
(f,Λ)=![]() (f(xk+1)-f(xk))|Δk|
(f(xk+1)-f(xk))|Δk|![]()
![]() |Λ|
|Λ|![]() (f(xk+1)-f(xk))=|Λ|(f(b)-f(a))→0 при |Λ|→0.
(f(xk+1)-f(xk))=|Λ|(f(b)-f(a))→0 при |Λ|→0.
3) f определена и
ограничена на [a,b], точки её разрыва м. б. покрыты конечным числом
интервалов с очень малой общей длиной (частный случай – конечное число точек
разрыва) ![]() f
f![]() R[a,b].
R[a,b].
Св-ва ∫ Римана
1) ![]() =b-a
=b-a
2) 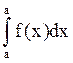 =0
=0
3) |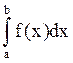 |
|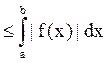
4) f(x)<g(x) ![]()
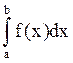 <
<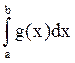
Сл-е ![]() f(x)(b-a)
f(x)(b-a)![]()
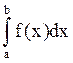
![]()
![]() f(x)(b-a)
f(x)(b-a)
5) ![]() (
(![]() fi(x))dx=
fi(x))dx=![]()
![]() fi(x)dx
fi(x)dx
6) f![]() R[a,b]
R[a,b] ![]()
![]()
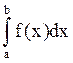 =
=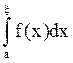 +
+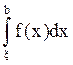
7) т. о среднем
f![]() R[a,b], m=
R[a,b], m=![]() f(x), M=
f(x), M=![]() f(x)
f(x) ![]()
![]() k
k![]() [m,M]
[m,M]
k(b-a)=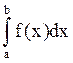
k=![]()
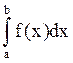 , k
, k![]() [m,M] по
сл-ю из 4).
[m,M] по
сл-ю из 4).
∫ и первообразная
Любая непрерывная на [a,b]
ф-я имеет на нём первообразную F(x)=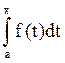 , x
, x![]() [a,b].
[a,b].
Ф-ла Ньютона-Лейбница: F(b)-F(a)=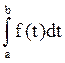
Интегрирование методом подстановки
Пусть 1) f(x) непрерывна на [a,b];
2) g(t)
нерерывна и дифференцирована на [c,d], g![]() [a,b]
[a,b]![]() t
t![]() [c,d];
[c,d];
3) a=g(c0), b=g(d0),
c0,d0![]() [c,d].
[c,d].
Тогда 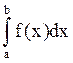 =
=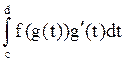 .
.
F’(x)=f(x)
![]()
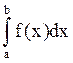 =F(b)-F(a)
=F(b)-F(a)
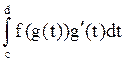 =
=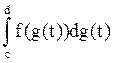 =F(g(d))-F(g(c))=
=F(g(d))-F(g(c))=
=F(b)-F(a)
Интегрирование по частям
Пусть u(x) и v(x)
непрерывны и непр-но диф-мы на [a,b]. Тогда 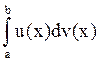 =u(x)v(x)|
=u(x)v(x)|![]() -
-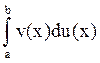 .
.
(u(x)v(x))’=u’(x)v(x)+u(x)v’(x)![]()
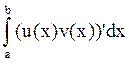 =
=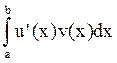 +
+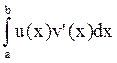 =
=
=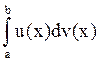 +
+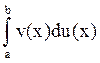
По
ф-ле Ньютона-Лейбница 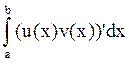 =u(x)v(x)|
=u(x)v(x)|![]()
Геометрич. приложения определённого ∫
Площадь криволинейной
трапеции (огранич. линиями x=a, x=b, y=0, y=f(x) ) S=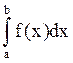 .
.
Длина кривой L=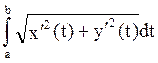 .
.
Объём тела с известным
поперечным сечением S(x) V=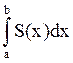 .
.
Объём тела вращения V=π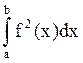
Несобственный интеграл
Несобственные ∫ с ∞ пределами -
I=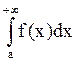 =
=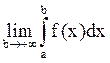 .
.
Если предел конечный, то I сходится, а f(x) интегрируема на [a,+∞), иначе I расходится.
Аналог-но 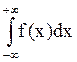 =
=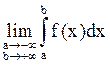 =
=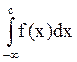 +
+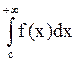 .
.
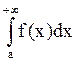 =F(x)
=F(x)![]() =F(+∞)-F(a), т. е. несобств. ∫ сущ-ет
=F(+∞)-F(a), т. е. несобств. ∫ сущ-ет ![]() сущ-ет
конечный
сущ-ет
конечный ![]() F(b)=F(+∞).
F(b)=F(+∞).
Св-ва
1) 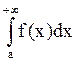 сходится
сходится ![]()
![]() b>a
b>a 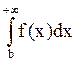 сходится.
сходится.
2) 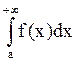 сходится
сходится ![]()
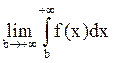 =0.
=0.
3) ![]() (
(![]() fi(x))dx сходится
fi(x))dx сходится ![]()
![]()
![]() fi(x)dx сходится.
fi(x)dx сходится.
Признаки сходимости
Если f(x)>0
![]() x , то Ф(А)=
x , то Ф(А)=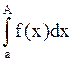 - монотонно возрастающая ф-я от А.
- монотонно возрастающая ф-я от А.
1) При f(x)≥0 ![]() x
x 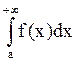 сходится
сходится ![]() при возрастающих А Ф(А)
ограничена сверху.
при возрастающих А Ф(А)
ограничена сверху.
2) Пусть x≥a, g(x)≥f(x).
Тогда 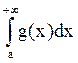 сходится
сходится ![]()
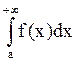 сходится;
сходится;
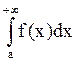 расходится
расходится ![]()
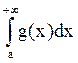 расходится.
расходится.
3) Пусть ![]()
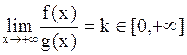 . Тогда
. Тогда 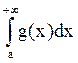 сходится, k<∞
сходится, k<∞ ![]()
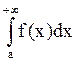 сходится;
сходится;
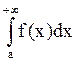 расходится, k>0
расходится, k>0 ![]()
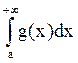 расходится.
расходится.
Признак Коши
Пусть для достаточно больших x f(x)=![]() , k>0,
g(x) ограничена. Тогда при k>1
, k>0,
g(x) ограничена. Тогда при k>1 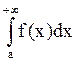 сходится; при k≤1
сходится; при k≤1 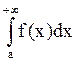 расходится.
расходится.
Критерий Коши
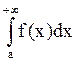 сходится
сходится
![]()
![]() ε>0
ε>0 ![]() B,C>a |
B,C>a |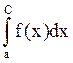 -
-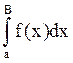 |=|
|=|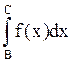 |<ε.
|<ε.
Cл-е Если сходится 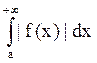 , то
, то 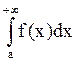 сходится.
сходится.
Абсолютная сходимость
Если сходятся I=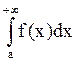 и
и 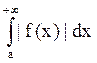 , то I –
абсолютно сходящийся, а f(x) – абс. интегрируемая на [a,+∞).
, то I –
абсолютно сходящийся, а f(x) – абс. интегрируемая на [a,+∞).
Если I=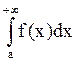 сходится, а
сходится, а 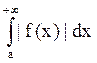 расходится,
то I – условно сходящийся.
расходится,
то I – условно сходящийся.
Если f(x) абс. интегрируема на [a,+∞), а g(x) ограничена, то (f(x)·g(x)) абс. интегрируема на [a,+∞).
Признак Абеля
Пусть f(x)
интегрируема на [a,+∞), 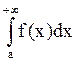 сходится
(м. б. не абс-но); g(x) монотонна и ограничена (|g(x)|≤L).
Тогда
сходится
(м. б. не абс-но); g(x) монотонна и ограничена (|g(x)|≤L).
Тогда 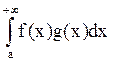 сходится.
сходится.
По
т. о среднем 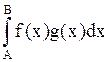 =g(A)
=g(A)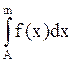 +g(A)
+g(A) 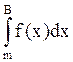 , A≤m≤B.
, A≤m≤B.
По
условию ![]() ε>0
ε>0 ![]() B,A>a |
B,A>a |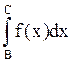 |<ε/2L
|<ε/2L
![]() |
|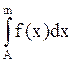 |<ε/2L,
|
|<ε/2L,
|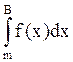 |<ε/2L.
|<ε/2L.
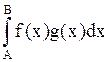 <ε
<ε
Признак Дирихле
Пусть f(x)
интегрируема в ![]() конечном [a,A],
конечном [a,A], 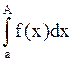 ограничен; g(x) монотонно →0
при x→∞. Тогда
ограничен; g(x) монотонно →0
при x→∞. Тогда 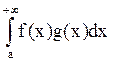 сходится.
сходится.
Несобственные ∫ от
неогранич. ф-ий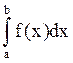 =
=![]()
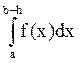 , где
b – особая точка,в к-й f(x) не
ограничена.
, где
b – особая точка,в к-й f(x) не
ограничена.
Точки ±∞ всегда особые.
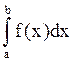 =F(x)
=F(x)![]() =F(b)-F(a), т. е. несобств. ∫ сущ-ет
=F(b)-F(a), т. е. несобств. ∫ сущ-ет ![]() сущ-ет
конечный
сущ-ет
конечный ![]() F(b-h)=F(b).
F(b-h)=F(b).
Признак сходимости
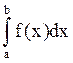 сходится
при f(x)>0
сходится
при f(x)>0 ![]()
![]() h>0
h>0 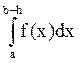 ≤const.
≤const.
Признак Коши
Пусть для x→b f(x)=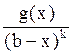 , k>0.
Тогда при k<1, g(x)≤C<∞
, k>0.
Тогда при k<1, g(x)≤C<∞ 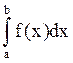 сходится;
при k≥1, g(x)≥C>0
сходится;
при k≥1, g(x)≥C>0 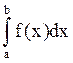 расходится.
расходится.
Св-ва
1) f(x)
интегр-ма в [b,a] ![]() f(x)
интегр-ма в [a,b] и
f(x)
интегр-ма в [a,b] и 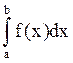 =
=
= -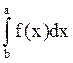 .
.
2) f(x)
интегр-ма в [a,b] ![]()
![]() х
х![]() [a,b]
[a,b] ![]() Ф(х)=
Ф(х)=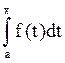 . При
этом если в х0 f(x) непрерывна, то
. При
этом если в х0 f(x) непрерывна, то ![]() Ф’(х)=f(x).
Ф’(х)=f(x).
Также вып-ся св-ва 3, 4, 5, 6 ∫ Римана.
Теоремы о среднем
1) Пусть f(x), g(x)
интегрируемы на [a,b] , m≤f(x)≤M , g(x) не
меняет знака. Тогда (f(x)·g(x)) интегрируемо на [a,b] , 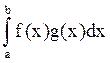 =k
=k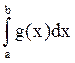 ,
где k
,
где k![]() [m,M].
[m,M].
2) Пусть f(x)
монотонна и ограничена на [a,b] , g(x) интегрируема на [a,b].
Тогда ![]()
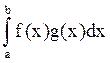 =f(a)
=f(a)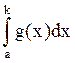 +f(b)
+f(b)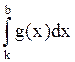 ,
где k
,
где k![]() [a,b].
[a,b].
Также для несобственных ∫
определено интегрирование по частям ( только ![]() ) и
замена переменных.
) и
замена переменных.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.