Изучение основных способов представления математических проблем в символьном виде, пригодном для формальной обработки на компьютере, страница 2

div(plus(X,B),plus(X,A)))))):-const(A,X), const(B,X),not(equal(A,B)),!. 

i(div(flt(F),mult(plus(X,A),plus(B,X))),X,mult(div(flt(F),minus(A,B)),ln(abs(

div(plus(X,B),plus(X,A)))))):-const(A,X), const(B,X),not(equal(A,B)),!. 

i(div(flt(F),mult(plus(A,X),plus(B,X))),X,mult(div(flt(F),minus(A,B)),ln(abs(

div(plus(X,B),plus(X,A)))))):-const(A,X), const(B,X),not(equal(A,B)),!.

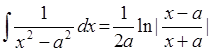
i(div(F,minus(potens(X,flt(2)),potens(A,flt(2)))),X,mult(div(F,mult(flt(2),A)),

ln(abs(div(minus(X,A),plus(X,A)))))):-const(A,X), const(F,X), !. 

i(div(F,minus(potens(A,flt(2)),potens(X,flt(2)))),X,mult(div(mult(

flt(-1),F),mult(flt(2),A)),ln(abs(div(minus(X,A),plus(X,A)))))):-const(A,X), const(F,X), !.

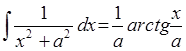
i(div(F,plus(potens(X,flt(2)),potens(A,flt(2)))),X,mult(div(F,A),atan(div(X,A)))):-const(A,X), const(F,X), !. 

i(div(F,plus(potens(A,flt(2)),potens(X,flt(2)))),X,mult(div(F,A),atan(div(X,A)))):-const(A,X), const(F,X), !.

3.  Интегралы от тригонометрических функций

i(sin(X),X,mult(flt(-1),cos(X))):-!.

i(cos(X),X,sin(X)):-!.

i(tan(X),X,mult(flt(-1),ln(abs(cos(X))))):-!.

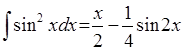
i(potens(sin(X),flt(2)),X,minus(div(X,flt(2)),div(sin(mult(flt(2),X)),flt(4)))):-!.

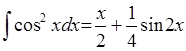
i(potens(cos(X),flt(2)),X,plus(div(X,flt(2)),div(sin(mult(flt(2),X)),flt(4)))):-!.

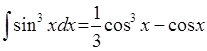
i(potens(sin(X),flt(3)),X,minus(div(potens(cos(X),flt(3)),flt(3)),cos(X))):-!.

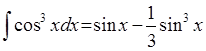
i(potens(cos(X),flt(3)),X,minus(sin(X),div(potens(sin(X),flt(3)),flt(3)))):-!.

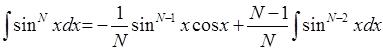
i(potens(sin(X),flt(N)),X,minus(div(mult(V,flt(K)),flt(N)),div(mult(

potens(sin(X),flt(K)),cos(X)),flt(N)))):-N1=trunc(N), N2=N-N1, N2=0, M=N-2, K=N-1, i(potens(sin(X),flt(M)),X,V),!.

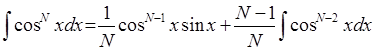
i(potens(cos(X),flt(N)),X,plus(div(mult(V,flt(K)),flt(N)),div(mult(

potens(cos(X),flt(K)),sin(X)),flt(N)))):-N1=trunc(N), N2=N-N1, N2=0, M=N-2, K=N-1, i(potens(cos(X),flt(M)),X,V),!.

4.  Интегралы от трансцендентных функций:

i(ln(X),X,minus(mult(X,ln(X)),X)):-!.

      

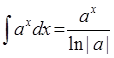
i(potens(A,X),X,div(potens(A,X),ln(abs(A)))):-const(A,X), !.

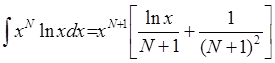
i(mult(X,ln(X)),X,mult(potens(X,flt(2)),minus(div(ln(X),flt(2)),div(flt(1),flt(4))))):-!.

i(mult(ln(X),X),X,mult(potens(X,flt(2)),minus(div(ln(X),flt(2)),div(flt(1),flt(4))))):-!.

i(mult(ln(X),potens(X,flt(N))),X,mult(potens(X,flt(M)),minus(div(ln(X),flt(M)),

div(flt(1),potens(flt(M),flt(2)))))):-N<>-1, M=N+1, !.

i(mult(potens(X,flt(N)),ln(X)),X,mult(potens(X,flt(M)),minus(div(ln(X),flt(M)),

div(flt(1),potens(flt(M),flt(2)))))):-N<>-1, M=N+1, !.

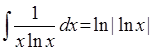
i(div(F,mult(X,ln(X))),X,mult(F,ln(ln(abs(X))))):-const(F,X), !.

i(div(F,mult(ln(X),X)),X,mult(F,ln(ln(abs(X))))):-const(F,X), !.

5.  Замена переменных:

i(mult(V,U),X,Y):-i(U,X,U1), doreduce(U1,U2), i(V,U2,Y), !.

i(mult(U,V),X,Y):-i(U,X,U1), doreduce(U1,U2), i(V,U2,Y), !.

4. Тестирование программы

1.  Исходное выражение:    (3.1+2*i)*x+4*sin(4*x)

Интеграл:                         x^2*i+1.55*x^2-cos(4*x)

2.  Исходное выражение:    tan(x^2)*2*x

Интеграл:                         (-1)*ln(|cos(x^2)|)

3.  Исходное выражение:    7.14*i/(z*x+c)

Интеграл:                         7.14*1/z*ln(|z*x+c|)*i

4.  Исходное выражение:    3*x*x*ln(x^3)

Интеграл:                         x^3*ln(x^3)-x^3

5.  Исходное выражение:    cos(x)*tan(x)*ln(-1*cos(x))

Интеграл:                         (-1)*cos(x)*ln((-1)*cos(x))+cos(x)

5. Текст программы (приложение)

DOMAINS

TOKL = STRING*

EXP=var(STRING);    flt(REAL);    plus(EXP,EXP);    minus(EXP,EXP);    mult(EXP,EXP);    div(EXP,EXP);    ln(EXP);    cos(EXP);

sin(EXP);     tan(EXP);     sec(EXP);     potens(EXP,EXP);    abs(EXP);    atan(EXP);    asin(EXP)

PREDICATES

run

diff

integr

d(EXP,STRING,EXP);

i(EXP,EXP,EXP);

const(EXP,EXP);

equal(EXP,EXP);

readexp(EXP);

readexp(EXP,string,integer)

check(EXP,TOKL,EXP);

writeexp(EXP);

strexp(EXP,string);

strPOTENS(EXP,string);

strMULT(EXP,string);

strMINUS(EXP,string);

strDIV(EXP,string);

strPAR(EXP,string);

tokl(STRING,TOKL);      /* Scanner */

front(STRING,TOKL,TOKL);

s_exp(TOKL,TOKL,EXP);   /* Parser */

Скачать файл